21. Гармонические колебания в резистивных, индуктивных и емкостных элементах

Резистивные цепи. Пусть к резистивному элементу R приложено гармоническое напряжение

. (3.21)

Согласно закону Ома через элемент R будет протекать ток

, (3.22)

где I_m = U_m/R – амплитуда;   _i =   _u – начальная фаза тока. Таким образом, ток i и напряжение и в резистивном элементе совпадают по фазе друг с другом (рис. 3.6, а). Средняя за период Т мощность, выделяемая в резисторе R,

. (3.23)

При последовательном или параллельном соединениях нескольких резистивных элементов ток в цепи определяется уравнением, аналогичным (3.22), где R определяется согласно (1.22) для последовательного и (1.27) для параллельного соединений элементов. При этом фазовый сдвиг между током и приложенным напряжением остается равным нулю.

Индуктивные цепи. Под действием напряжения (3.21) в индуктивном элементе будет протекать ток согласно (1.9):

, (3.24)

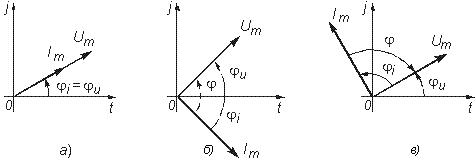
Рис.3.6

где I_m = U_m/(  L) = U_m/X_L; X_L =   L – индуктивное сопротивление;   _i =   _u –   /2 – начальная фаза тока.

Величину, обратную X_L, называют индуктивной проводимостью B_L = 1/(  L). Как следует из полученных выражений, ток в индуктивности отстает от приложенного напряжения на   /2, т. е. фазовый сдвиг между током i и напряжением и (рис. 3.6, б)

. (3.25)

При последовательном и параллельном соединениях индуктивных элементов ток в цепи определяется уравнением, аналогичным (3.24), где L находится согласно (1.23) для последовательного и (1.29) для параллельного соединений.

Емкостные цепи. Для емкостного элемента согласно уравнению (1.12) имеем:

, (3.26)

где I_m =   CU_m = B_CU_m; B_C =   C – емкостная проводимость;   _i = =   _u +   /2 – начальная фаза тока. Величину, обратную B_C, называют емкостным сопротивлением X_C = 1/( C). Фазовый сдвиг между током и напряжением на емкостном элементе

. (3.27)

Из приведенных уравнений следует, что ток в емкости опережает приложенное напряжение на угол   /2 (рис. 3.6, в), причем знак “–” свидетельствует об отставании напряжения и от тока i. Средняя за период мощность в емкостной цепи также равна нулю.

22. Гармонические колебания в цепи при последовательном соединении r, l, с-элементов

Допустим, что в цепи, содержащей последовательно соединенные элементы R, L, С (рис. 3.7), протекает ток

. (3.28)

Согласно ЗНК напряжение на отдельных участках цепи определяется уравнением

. (3.29)

Подставив в (3.29) значение тока из (3.28), получим

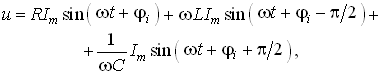
или

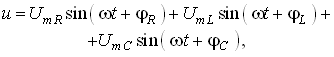 (3.30)

где

 (3.31)

Напряжение U_mR на резистивном сопротивлении R называется активной составляющей приложенного напряжения и обозначается U_ma = U_mR, разность напряжений U_mp = U_mL – U_mC называется реактивной составляющей. Согласно этому определению и формулам (3.31) имеем:

. (3.32)

Рис. 3.7

Рис. 3.8

Рис. 3.9

Величина X = X_L – X_C =   L – 1/(  C) называется реактивным сопротивлением, а величина

 (3.33)

– полным сопротивлением цепи.

Треугольник на векторной диаграмме, образованный напряжениями U_ma, U_mp, U_m называют треугольником напряжений.