15. Методика изучения приемов письменного деления на однозначное число в концентре «Многозначные числа»

При делении необходимо примеры подбирать так, чтобы выс­ший разряд делимого делился на делитель (был больше его). На таких примерах удобнее всего закрепить предварительную прикид­ку числа цифр в частном, о которой учащиеся уже получили представление при делении чисел в пределах 1000. 232

Затем подбираются примеры, в которых высший разряд делимого не делится нацело на делитель 12 575:5 (один десяток тысяч не делится на 5). Тогда на 5 делим 12 единиц тысяч. В частном будет четырехзначное число. Ставим 4 точки в частном, начинаем делить 12 ед. тысяч на 5 и т. д. Необходимо работать в этот период над закреплением алгорит­ма деления.

Чтобы ученики лучше запомнили последовательность рассуждений при выполнении этого действия, полезно использо­вать схему, в которой это подробно излагается:

1) прочитай и запиши пример;

2) выдели первое неполное делимое;

3) определи количество цифр в частном и поставь на их месте точки;

4) раз­дели неполное делимое и запиши полученное число в частное;

5) умножь это число на делитель, чтобы узнать, какое число ты разделил;

6) вычти, чтобы узнать, сколько еще единиц осталось разделить; остаток должен быть меньше делителя;

7) остаток вы­рази в единицах низшего разряда и прибавь к нему единицы такого же разряда делимого;

8) деление так же продолжай до полного решения примера;

9) сопоставь частное и делимое; част­ное должно быть меньше делимого;

10) проверь ответ действием умножения. Этой схемой учитель пользуется при объяснении деления, учит ею пользоваться учащихся. Сначала учащиеся читают по схеме каждое задание и отвечают. Затем задание читается ими про себя, а ответ произносится вслух. Наконец, учащиеся пользуются этой схемой самостоятельно, учитель может помогать учащимся лишь наводящими вопросами. Особое внимание следует уделить таким случаям деления, в которых нули получаются в середине или на конце частного.

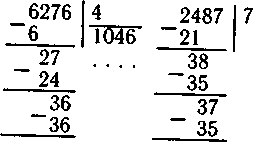
16. Методика изучения приемов письменного деления на двузначное и трехзначное число в концентре «Многозначные числа»

Первое знакомство с этим видом деления проис­ходит на примерах внетабличного деления, а именно при делении двузначного числа на двузначное, когда в частном получается однозначное число. В этом случае частное отыскивается приемом округления делимого и делителя до круглых чисел. Например: «При отыскании частного 93:31 округляем делимое 93 до 90, делитель 31 до 30. Тогда 90:30=3. Значит, в частном надо взять по 3. Проверяем: 31x3=93. Ответ верен. Однако, как показывает опыт, такие рассуждения и множество промежуточных вычислений доступны не всем учащимся. Поэтому целесообразно учащихся познакомить с приемом деления, который доступен большинству школьников, если они овладели приемом умножения двузначного числа на однозначное. Учитель показывает, что при делении на двузначное число труд­нее всего правильно подобрать цифру частного.

Далее последовательно рассматривается деление трех-, четырех-, пяти- и шестизначных чисел на двузначное число. При решении всех этих примеров необходимо учитывать, что отделяемые две цифры делимого составляют число, которое либо равно, либо больше делителя, и только после этого рассматриваются случаи, когда это число меньше делителя, и в этих случаях требуется отделить три цифры делимого.

Рассматриваются и случаи деления с остатком:

Вслед за делением с остатком рассматривается деление трех­значного числа на двузначное, когда в частном получается дву­значное число. Вначале в делимом подбираются такие числа, в которых первое неполное делимое состояло бы из двух цифр, а делитель состоял из цифр, не превышающих 5. И наконец, рассматриваются такие случаи деления: число, со­стоящее из двух цифр делимого, не делится на делитель.

Рассуждения проводятся так: «17 тысяч не де­лятся на 43, тогда на 43 разделим 178 сотен. В частном получится трехзначное число — ставим 3 точки. Делитель 43 заменим меньшим круглым числом 40. Делим 178 на 40. Берем в делимом первые две цифры, а в делителе первую цифру. Получаем делимое 17, а делитель 4. 17 делим на 4. Берем по 4, проверяем умножением и т. д.».