4.2. Парный регрессионный анализ.

Наряду с оценкой направления и тесноты связи, статистика выражает аналитически взаимосвязь между факторным и результативным признаками с помощью уравнения регрессии, которое показывает форму связи между и и имеет вид математической функции.

Наиболее распространенные функции для выражения формы связи:

(уравнение прямой (линейная))

(парабола второго порядка)

(гипербола)

(показательная)

(степенная)

Если выбрана линейная функция: – показывает, на сколько единиц изменяется результативный признак , при увеличении факторного признака на единицу.

Если – то связь прямая

– то связь обратная

Если имеет положительное значение, то связь прямая, если отрицательное значение, то связь обратная.

Этапы построения уравнения парной регрессии:

1. Проверка однородности совокупности по каждому из признаков, а также близости распределений каждого из признаков к нормальному закону распределения вероятностей.

2. Строится график корреляционного поля – исходные данные переносим на график:

   1. оценка наличия направления связи:

связь есть и она прямая

связь есть и она обратная

связь либо отсутствует, либо настолько слаба, что нет смысла ее оценивать

2. выявление и исключение (выбраковка) аномальных единиц наблюдения (значения).

фактические значения

аномальные значения

теоретические значения

доверительный интервал

Рис. 1. Корреляционное поле.

3. подбор математической функции по характеру концентрации единиц на корреляционном поле. Например, можно предположить, что наблюдается линейная зависимость между и .

1. Если и имеют разные единицы измерения, то необходима стандартизация, т.е. пересчет по каждому из признаков в стандартизованный масштаб:

№ п/п	,	, руб.
1 2 3 4 5* .
Итого

* – такое-то (единица) наблюдение исключено из общего анализа, т.к. считается аномальной.

По каждому признаку необходимо рассчитать среднее значение и среднее квадратическое отклонение.

4. Составление системы нормальных уравнений:

Для уравнения прямой:

5. Промежуточные расчеты.

6. Вычисление параметров уравнения с точностью до 3, 4 знаков после запятой:

(в нашем примере: увеличение на 1 вызывает рост на 5 тыс. 348,2 руб.)

7. Расчет теоретических значений результативного признака .

8. Проверка правильности расчетов: (допускается небольшое отклонение).

9. Для подтверждения значимости построенного уравнения вычисляем соответствующий параметрический показатель тесноты связи ( 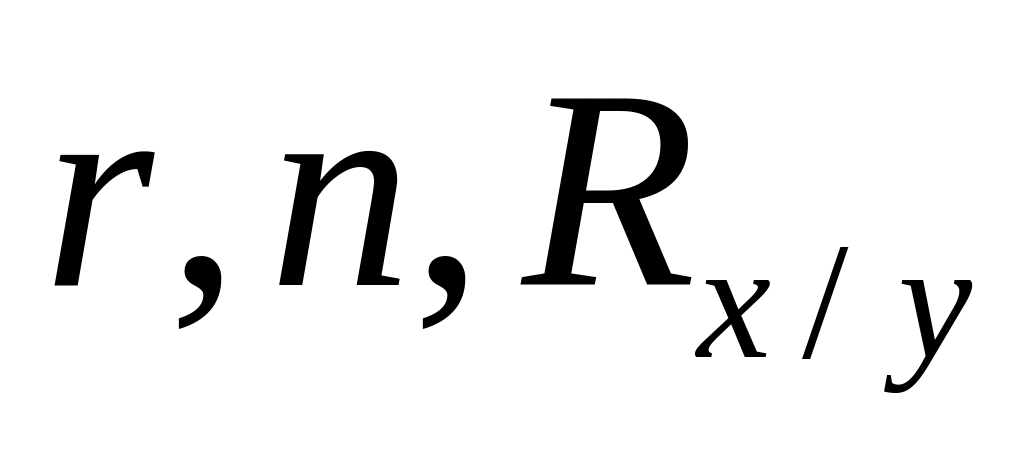– индекс корреляции) и делаем выводы.

10. Оценка уравнений регрессии:

    1. визуальная оценка: переносим теоретические значения результативного признака на график корреляционного поля и визуально определяем, насколько удачно выбранная функция описала сложившуюся взаимосвязь между и .

    2. математическая оценка – это проверка точности (достоверности) уравнения регрессии: есть разные критерии:

       1. остаточное средне квадратическое отклонение теоретических значений от фактических:

2. средняя ошибка аппроксимации:

Чем меньше значение, тем лучше (тем точнее уравнение регрессии, тем точнее описывает взаимосвязь).

11. интерпретация результатов (выводы).