
- •Тема 5. Индексный метод анализа.
- •1. Сущность, значение, задачи индексов.
- •2. Классификация индексов.
- •3. Индивидуальные индексы.
- •4. Общие (агрегатные) индексы.
- •5. Средние (преобразованные) индексы.
- •6. Индексы переменного и постоянного состава, индексы структурных сдвигов.
- •7. Индексы с постоянными и переменными весами с постоянной и переменной базой сравнения.
- •8. Взаимосвязи индексов.
- •9. Территориальные индексы.
- •10. Биржевые индексы.
- •Тема 6. Статистическое изучение связи между явлениями.
- •1. Виды взаимосвязей между явлениями.
- •4.2. Парный регрессионный анализ.
9. Территориальные индексы.
Эти индексы строятся не во времени, а в пространстве, и позволяют сравнить величину явления в разных регионах или странах. При их построении возникают обычные проблемы с выбором весов (соизмерителей).
Пример: сравнить индекс цен в городе А и Б:
![]()
![]()
При построении территориальных индексов необходимо применить стандартизированные веса:
![]() – в качестве
стандартного веса в данном индексе
выступает суммарное количество каждого
из товаров в городе А и Б.
– в качестве
стандартного веса в данном индексе
выступает суммарное количество каждого
из товаров в городе А и Б.
![]()
(По товарам представителем)
![]()
![]()
10. Биржевые индексы.
Следует различать индексы товарно-сырьевой биржи (см. учебник «Статистика рынка товаров и услуг» под ред. Белявского) и индексы фондовой биржи (см. рынок ценных бумаг).
Тема 6. Статистическое изучение связи между явлениями.
Виды взаимосвязей между явлениями.
Задачи статистики по изучению связи.
Методы изучения связи.
Корреляционно-регрессионный метод анализа:
Парный корреляционный анализ.
Парный регрессионный анализ.
Множественные корреляции и регрессии.
1. Виды взаимосвязей между явлениями.
Изучаемые статистикой явления формулируются и развиваются за счет действия на них многих факторов.
Статистика при помощи различных методов выявляет эти факторы, определяет наличие связи и форму зависимости между ними.
Основные виды связи:
балансовая;
компонентная;
факторная.
Балансовая связь характеризует зависимость между источниками формирования ресурсов и их использованием:
![]()
предложение = использование ресурсов
остатки на начало + прибытие = выбытие + остатки на конец периода
Компонентные связи характеризуют изменение статистического показателя за счет изменения компонентов, его образующих.
![]()
![]() – результативный
признак,
– результативный
признак,
![]() и
и
![]() – факторные признаки
– факторные признаки
Факторные связи проявляются в согласованной вариации изучаемых показателей.
![]() – факторный признак
– факторный признак
![]() – результативный
признак (испытывает влияние факторных
признаков)
– результативный
признак (испытывает влияние факторных
признаков)
Факторные связи принято классифицировать по степени зависимости одного явления от других:
Функциональная связь – связь, при которой величины результативного признака
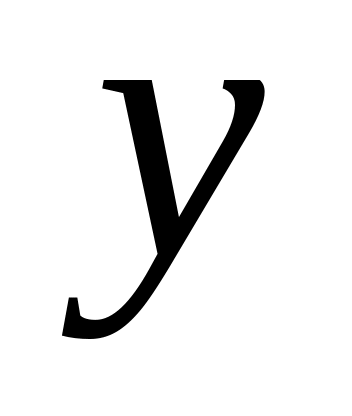 полностью определяется величиной
факторного признака
полностью определяется величиной
факторного признака
 .
.
![]()
Функциональные связи чаще всего встречаются в технике, математике и других точных науках.
Корреляционная (статистическая) связь – проявляется в массовых явлениях общественной жизни. В этом случае нет точного соответствия и .
Одному значению факторного признака может соответствовать несколько значений результативного признака , т.к. на результативный признак воздействует еще множество других факторных признаков.
![]() ,
,
где
![]() – влияние общих неучтенных факторов.
– влияние общих неучтенных факторов.
Таким образом, влияние факторного признака проявляется лишь в общем, среднем для всей совокупности.
По направлению связи бывают:
прямые;
обратные.
По аналитическому выражению:
линейные (прямолинейные);
нелинейные (криволинейные).
Различают также парные, множественные связи:
![]()
![]()
2. Задачи статистики по изучению связи.
выявить наличие связи между явлениями;
установить направление связи;
оценить тесноту связи;
Эти задачи решает корреляционный анализ (метод корреляции).
выразить связь аналитически – метод регрессии.
3. Методы изучения связи.
м

см. (самостоятельно, знать)
етод сопоставления двух параллельных рядов;графический;
метод аналитической группировки;
балансовый;
метод дисперсионного анализа;
метод корреляционной таблицы;
метод корреляционно-регрессионного анализа.
4. Корреляционно-регрессивный анализ.
4.1. Парный корреляционный анализ.
Упрощенная схема парного корреляционно-регрессионного анализа:
Близость распределения к нормальному
закону распределения вероятностей (N
(1;0))

да да да




регрессионный
анализ
 нет
нет нет
нет
нет нет
непараметрические
показатели
параметрические
показатели
корреляционный
анализ

 Парный
корреляционный анализ заключается в
вычислении подходящего показателя
тесноты связи в зависимости от исходной
информации. Полученный результат
расчетов обычно сравнивают со шкалой
Чеддока, которая позволяет сделать
вывод о степени зависимости между
изучаемыми признаками:
Парный
корреляционный анализ заключается в
вычислении подходящего показателя
тесноты связи в зависимости от исходной
информации. Полученный результат
расчетов обычно сравнивают со шкалой
Чеддока, которая позволяет сделать
вывод о степени зависимости между
изучаемыми признаками:
Шкала Чеддока:
Значение коэффициента корреляции |
0,1 – 0,3 |
0,3 – 0,5 |
0,5 – 0,7 |
0,7 – 0,9 |
0,9 – 0,99 |
Характеристика тесноты связи |
Слабая |
умеренная |
Заметная |
высокая |
весьма высокая |
I. Параметрические показатели тесноты связи: если есть возможность провести регрессионный анализ, то для оценки тесноты связи вычисляются параметрические показатели (коэффициенты (см. блок-схему)). К ним относятся:
Линейный коэффициент корреляции:

– факторный признак
– результативный признак
![]() – число наблюдений
– число наблюдений
Значения всегда (-1;+1)
Если значение
![]() :
:
 – прямая
– прямая – обратная
– обратная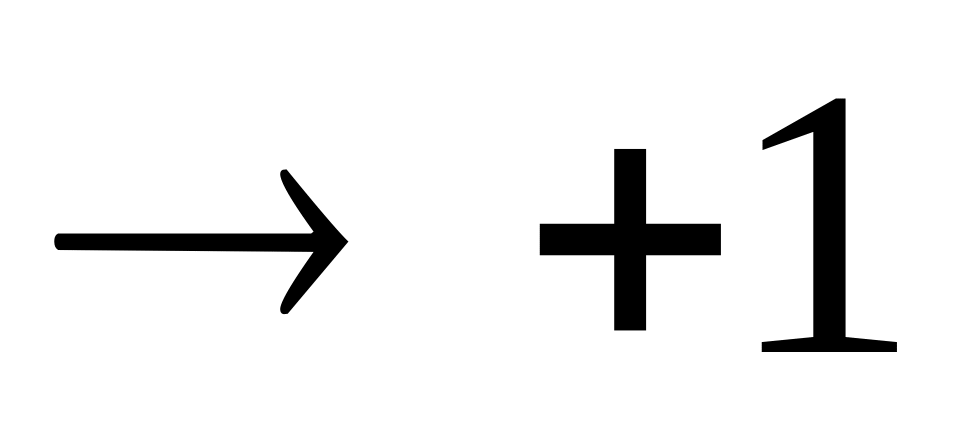 и
и
 – сильная
– сильная – слабая
– слабая
Этот коэффициент применяется, если в регрессионном анализе была выявлена прямолинейная зависимость между и .
К
 орреляционное
отношение:
орреляционное
отношение:


Индекс корреляции:
 (0;+1)
(0;+1)
Они применяются, если в регрессионном анализе выявлена криволинейная зависимость между и . Для вычисления данных показателей рассчитываются предварительно 3 вида количественной дисперсии:
 – отражает вариацию
результативного признака
за счет действия факторного признака
;
– отражает вариацию
результативного признака
за счет действия факторного признака
;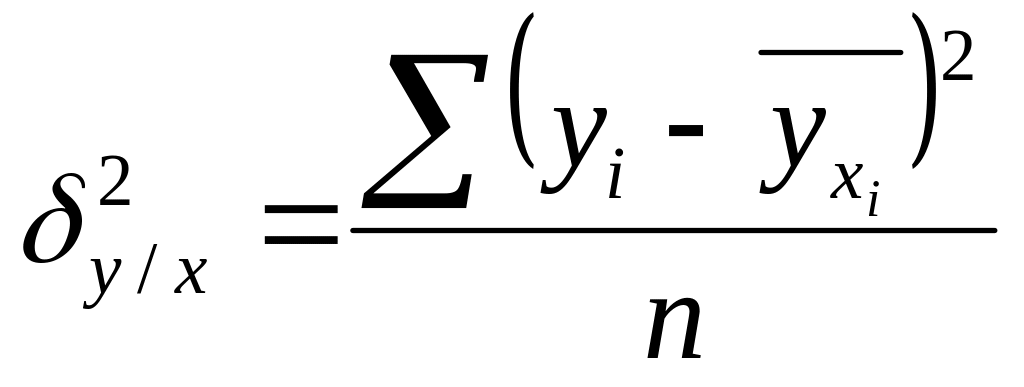 – отражает вариацию
за счет всех факторов кроме
.
– отражает вариацию
за счет всех факторов кроме
. – отражает вариацию
за счет действия всех факторов.
– отражает вариацию
за счет действия всех факторов.
II. Непараметрические показатели тесноты связи: показатели данной группы вычисляют для количественной оценки тесноты связи. Если нет возможности применить регрессионный анализ.
Коэффициент Фехнера (самый простой):
![]() (–1;+1)
(–1;+1)
Его вычисляют для
двух количественных признаков:
![]() – это сумма совпадающих знаков в
отклонениях от средних по рядам,
– это сумма совпадающих знаков в
отклонениях от средних по рядам,
![]() – это сумма несовпадающих знаков в
отклонениях от средних по рядам.
– это сумма несовпадающих знаков в
отклонениях от средних по рядам.
№ п/п |
|
|
|
|
|
|
1 2 3 4 . . |
|
|
+ – + – . . |
+ – – + . . |
1 1 0 0 . . |
0 0 1 1 . . |
и – значение признаков у каждой единицы наблюдения
Коэффициент ассоциации Юла: применяются для оценки тесноты связи между двумя альтернативными признаками:
![]() (–1;+1)
(–1;+1)
|
Да |
Нет |
Да |
|
|
Нет |
|
|
![]() – соответствующие
поля «матрицы четырех полей»
– соответствующие
поля «матрицы четырех полей»
Коэффициент контингенции Пирсона вычисляется вместо коэффициента ассоциации в случае, когда одно из полей матрицы равно 0. Дает более осторожную оценку тесноте связи (как правило,
 на
1/3 всегда меньше
на
1/3 всегда меньше
 ,
т.к. если в матрице одно из полей равно
0,
либо
+, либо –).
,
т.к. если в матрице одно из полей равно
0,
либо
+, либо –).
![]() (–1;+1)
(–1;+1)
Коэффициенты взаимной сопряженности:
П ирсона:
![]() (0;+1)
(0;+1)
Ч
 упрова:
учитывает, на сколько
упрова:
учитывает, на сколько
групп разбит каждый из признаков
(более предпочтителен).
 (0;+1)
(0;+1)
Вычисляются в случае, если каждый из признаков и разбит на 2 группы и более (признаки могут быть как качественными, так и количественными). По данным коэффициентам можно сделать вывод только о тесноте связи, о направлении связи – нельзя.
![]() и
и
![]() – число групп по каждому из признаков
– число групп по каждому из признаков
Методика расчета
![]() :
:
Группа по признаку |
Группа признаков |
|
|
||
1 |
2 |
3 |
|||
1 |
4 16 + |
+ |
= |
= |
* + |
2 |
+ |
+ |
= |
= |
* + |
3 |
+ |
+ |
= |
= |
* = |
Итого |
|
|
|
|
|
– частоты (3 х 3)
в клетках под каждой частотой записываем ее квадрат;
полученный результат делим на итог частот данного столбца;
суммируем полученные значения в строчках и результат записываем в первом итоговом столбце;
полученные значения делим на сумму частот данной строки, и результат записываем во второй итоговый столбец;
суммируем полученные значения * - это величина и есть .
Ранговый коэффициент корреляции (или коэффициент корреляции рангов):
К. Спирмэна
![]() (–1;+1)
(–1;+1)
– ранговая разность
– число наблюдений (единиц совокупности).

М. Кендалла
![]() (–1;+1)
(–1;+1)
Методика Спирмэна:
Ранжируем единицы наблюдения по признаку (ранжирование – это перегруппировка исходных данных – расположение единиц наблюдения в порядке возрастания или убывания значений):
№ п/п |
|
|
. . |
. . |
. . |
Формируем новую таблицу по – по возрастанию:
№ п/п |
|
|
|
|
|
|
25 16 3 8 14 |
13,8 13,9 13,9 14,2 14,4 … …. |
1,8 1,9 2,2 1,9 2,6 … … |
1 2,5 2,5 4 5 … … |
1 2,5 4 2,5 5 … … |
|
|
Проставляем ранги сначала для , затем для : ранг – это порядковый номер варианта в упорядоченной совокупности. Связанные ранг – 13,9 и 13,9, сл.,
 .
Ранги хороши тем, что нет единиц
измерения;
.
Ранги хороши тем, что нет единиц
измерения;Предварительные выводы:
если с ростом ранга возрастает ранг , то связь есть – она прямая;
Если с ростом ранга уменьшается ранг , связь есть – она обратная;
если с ростом ранга невозможно отследить закономерность изменения ранга , то связь либо отсутствует вообще, либо настолько слаба, что нет смысла ее оценивать.
вычисляем ранговую разность и ее квадрат ;
подстановка в формулу + выводы из 3 частей: есть/нет, прямая/обратная, сильная/слабая).
В некоторых случаях вычисляются другие непараметрические показатели, например, коэффициент канкордации, песериальный коэффициент корреляции.






