Тема 30 Потери энергии на местных сопротивлениях в автомодельной области

В местных сопротивлениях имеют место дополнительные потери напора, которые определяются по формуле Вейсбаха (29.1) или (29.2):

 потери напора, м

h_м =  × ;

 потери давления, Па

р_м =  ×  × ,

где v – средняя скорость в сечении, обычно после местного сопротивления, м/с;

 – коэффициент местного сопротивления, безразмерный;

 – плотность жидкости, кг/м³;

g – ускорение силы тяжести, м/с².

При развитом турбулентном режиме течения в автомодельной области коэффициент  от числа Рейнольдса не зависит, а зависит от вида местного сопротивления, его геометрической формы и размеров препятствий на пути потока (иначе, геометрии потока).

Рассмотрим некоторые случаи местных гидравлических сопротивлений при турбулентном течении в автомодельной области и напорном движении.

1. Внезапное расширение трубопровода (рис. 52). Сечение трубопровода внезапно расширяется от площади ₁ до площади ₂. В месте расширения поток отрывается от твёрдых стенок, образуя транзитную струю, которая постепенно расширяется. На некотором расстоянии от кромки расширения транзитная струя заполнит сечение ₂. Между стенкой трубы и поверхностью транзитной струи жидкость медленно вращается, образуя водоворотную область. На границе между транзитной струёй и водоворотной областью происходит интенсивное вихреобразование. В связи с интенсивным вихреобразованием на границе транзитной струи и последующим гашением вихрей, происходят потери удельной энергии при внезапном расширении, которые можно определить по формуле Вейсбаха (29.1) или (29.2).

Коэффициенты сопротивления при внезапном расширении потока определяются следующими выражениями:

 коэффициент, отнесённый к средней скорости v₁ в сечении 1-1 (до местного сопротивления)

_{в.р. 1} = ; (30.1)

 коэффициент, отнесённый к средней скорости v₂ в сечении 2-2 (после местного сопротивления)

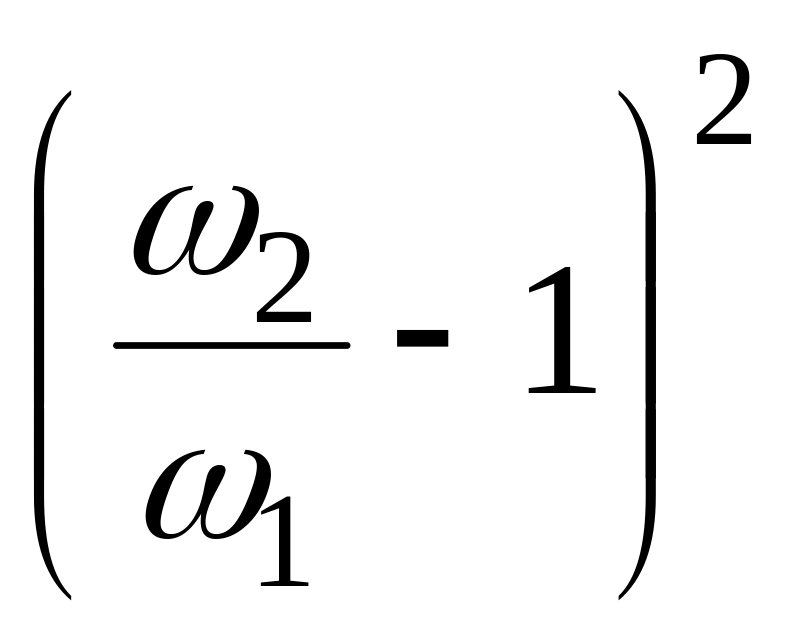_{в.р. 2} = . (30.2)

где ₁ – площадь поперечного сечения трубопровода до расширения, м²;

₂ – площадь поперечного сечения трубопровода после расширения, м².

Рисунок 52 – Внезапное расширение Рисунок 53 - Диффузор

При Re  5×10³ коэффициенты сопротивления при внезапном расширении зависят только от отношения площадей ₁ и ₂.

Потери удельной энергии при внезапном расширении трубопровода могут быть определены также по формуле Борда:

 потери напора, м

h_в.р. = ; (30.3)

 потери давления, Па

р_в.р. =  × , (30.4)

где v₁ – средняя скорость в сечении до местного сопротивления, м/с;

v₂ – средняя скорость в сечении после местного сопротивления, м/с;

 – коэффициент Кориолиса.

Потери напора при внезапном расширении равны скоростному напору, соответствующему потерянной скорости (v₁ – v₂).

Если принять  = 1, формулы (30.3) и (30.4) принимают вид:

 потери напора, м

h_в.р. = ; (30.3, а)

 потери давления, Па

р_в.р. =  × , (30.4, б)

2. Постепенное расширение (диффузор) (рис. 53).Потери удельной энергии в диффузорах разделяют на потери, связанные с постепенным расширением сечения и потери на трение по длине диффузора. Соответственно коэффициент сопротивления диффузора _д условно делится на коэффициенты сопротивления постепенного расширения _п.р. и по длине _дл.:

_д = _п.р. + _дл. = k_д × _в.р. + _дл..

Вследствие малости потерями удельной энергии по длине диффузора часто пренебрегают (_дл.  0). Поэтому принимаем, что коэффициент сопротивления диффузора равен коэффициенту сопротивления на постепенное расширение (_д = _п.р.).

Коэффициенты сопротивления диффузора обычно относят к скорости в первом сечении v₁ (до местного сопротивления). Тогда коэффициент сопротивления диффузора равен:

_д = k_д × _{в.р. 1} = k_д × . (30.5)

где k_д – коэффициент смягчения диффузора;

Коэффициент смягчения диффузора k_д учитывает уменьшение потерь энергии на диффузоре по сравнению с внезапным расширением при том же соотношении сечений соединяемых труб. Коэффициент k_д находится по справочным таблицам в зависимости от угла конусности диффузора .

Потери удельной энергии на диффузоре по формуле Борда (при  = 1) равны:

 потери напора, м

h_в.р. = k_д × ; (30.6)

 потери давления, Па

р_в.р. = k_д ×  × , (30.7)

В зависимости от угла конусности движение в диффузоре может быть безотрывным (при   8⁰…10⁰), либо может происходить отрыв потока от стенок на части длины диффузора (при  10⁰    50⁰…60⁰). Полный отрыв потока от стенок по всей длине диффузора наблюдается при   50⁰…60⁰. Отрыв бывает несимметричным и даже односторонним. Наивыгоднейший угол конусности изменяется в пределах от 5⁰до 8⁰.

3. Внезапное сужение (рис. 54). При внезапном сужении за кромкой сужения происходит отрыв потока от стенки и образование транзитной струи, которая сначала испытывает сжатие, а затем расширение. Между твёрдой стенкой и поверхностью транзитной струи образуется водоворотная зона. Образуются вихри, которые в результате обмена жидкостью между водоворотной зоной и транзитной струёй проникают в поток, где гасятся трением. В результате работы сил трения часть механической энергии потока переходит в теплоту. Потери удельной энергии равны:

h_в.с. =  × или р_в.с = _в.с ×  × .

Рисунок 54 – Внезапное сужение Рисунок 55 - Конфузор

Коэффициент местного сопротивления на внезапном сужении _в.с при Re  110⁴ зависит только от отношения площадей . Значение коэффициента _в.с можно определить по формуле

_в.с. = (30.8)

где   коэффициент сжатия струи.

Коэффициент сжатия струи равен отношению минимального живого сечения потока _с к площади трубопровода меньшего сечения ₂

 = , (30.9)

где _с  минимальное живое сечение потока;

₂  площадь трубопровода меньшего сечения ₂ (после местного сопротивления).

Коэффициент сжатия струи  зависит от степени сжатия потока n и его можно оценить по эмпирической формуле:

 = 0,57 + . (30.10)

где n – степень сжатия потока.

Степень сжатия потока n представляет собой отношение площади трубопровода меньшего сечения ₂ (после местного сопротивления) к площади трубопровода большего сечения ₁ (до местного сопротивления):

n = . (30.11)

4. Постепенное сужение (конфузор) (рис. 55). При движении жидкости в конфузоре скорость потока вдоль трубопровода возрастает, а давление уменьшается. Так как жидкость движется от большего давления к меньшему, то причин для срыва потока (как это имело место в диффузоре) в конфузоре меньше. Отрыв потока от стенок с небольшим сжатием возможен на выходе из конфузора. Поэтому сопротивление конфузора всегда меньше сопротивления диффузора с теми же геометрическими характеристиками.

Потери удельной энергии в конфузоре складываются из потерь на постепенное сужение сечения и потерь на трение по длине конфузора. Соответственно коэффициент сопротивления конфузора _к условно делится на коэффициенты сопротивления постепенного сужения _п.с. и по длине _дл.:

_к = _п.с. + _дл. = k_к × _в.с. + _дл..

Вследствие малости потерями удельной энергии по длине конфузора часто пренебрегают ( 0). Поэтому принимаем, что коэффициент сопротивления конфузора равен коэффициенту сопротивления на постепенное сжатие (_к = _п.с.).

Коэффициент сопротивления конфузора _к равен:

_к = k_к × _в.с. = k_к × , (30.12)

где k_к – коэффициент смягчения конфузора.

Коэффициент смягчения конфузора k_к учитывает уменьшение коэффициента _в.с., а следовательно, потерь энергии на конфузоре по сравнению с внезапным сужением при том же соотношении сечений соединяемых труб. Коэффициент k_к зависит от угла конусности конфузора .

5. Поворот (рис. 56). В результате искривления потока на вогнутой стороне внутренней поверхности трубы давление больше, чем на выпуклой. В связи с этим в направлении течения создаются различия в скорости, способствующие отрыву потока от стенок. Это приводит сначала к сужению струи, а затем – далее по течению – к её расширению. При этом возникают значительные потери удельной энергии.

Рисунок 56  Поворот

При резком повороте трубы, который называется также простым или острым коленом (незакруглённое колено), потери удельной энергии особенно велики. Для гладких стенок труб с круглым и квадратным поперечным сечением при Re  210⁵ коэффициент сопротивления поворота _{пов. р.} зависит только от угла поворота .

При плавном повороте трубы (закруглённое колено, отвод) вихреобразование уменьшается и потери удельной энергии будут значительно меньше. Коэффициент сопротивления поворота _пов. зависит от угла поворота, а также от отношения радиуса закругления R_п к диаметру трубы d и от величины коэффициента гидравлического трения .

Коэффициент сопротивления при плавном повороте трубопровода на произвольный угол  определяется по формуле:

_пов. = а × ₉₀, (30.13)

где а – справочный коэффициент, зависящий от угла поворота;

₉₀ – коэффициент местного сопротивления при плавном повороте трубы на 90⁰.

Коэффициент местного сопротивления при плавном повороте трубы на 90⁰ определяют по эмпирической формуле Альтшуля:

₉₀ = , (30.14)

где d – диаметр трубопровода, м;

R_п – радиус закругления трубы, м;

  коэффициент гидравлического трения.