
Вариант 19
Задание 1
Даны матрицы А и В. Найти: а)произведение матриц А и В; б) определитель матрицы А; в) матрицу, обратную к матрице А.
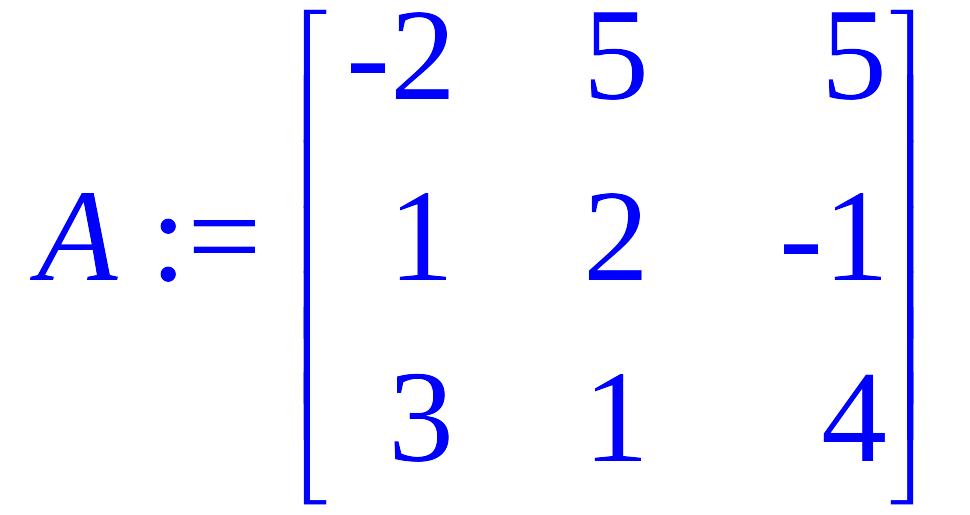
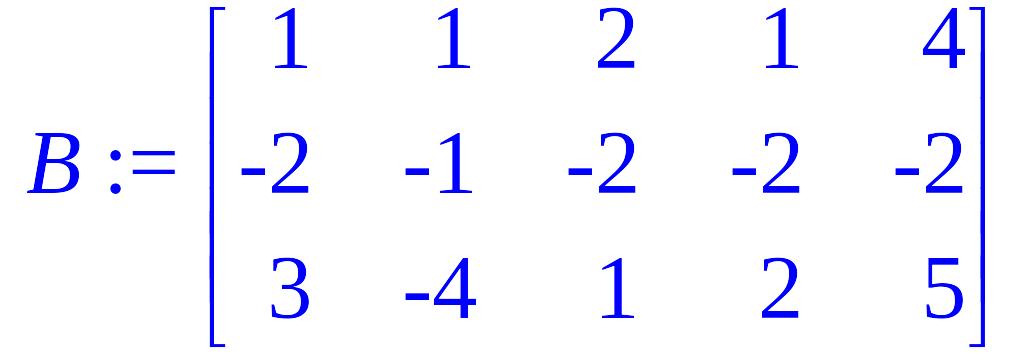
Задание 2
Решите систему линейных алгебраических уравнений а) методом обратной матрицы; б)методом Крамера; в)методом Гаусса.
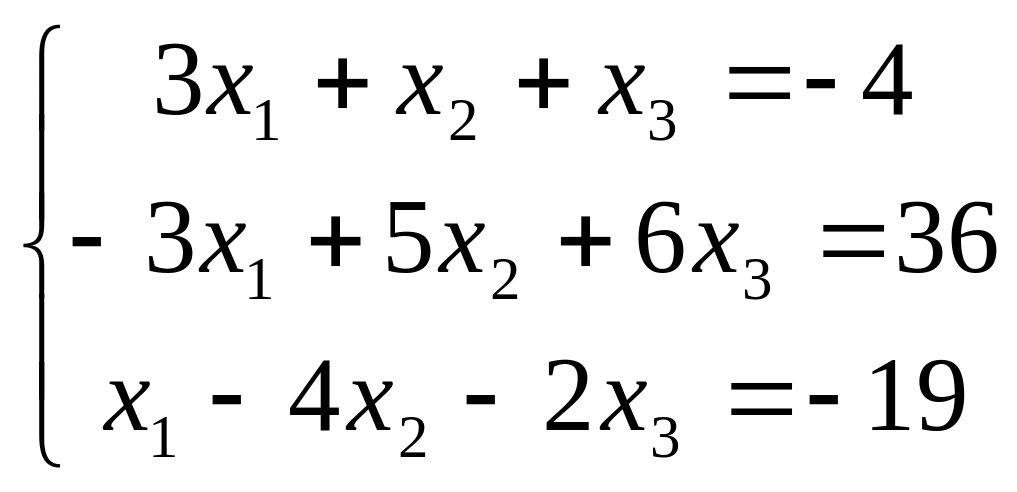
Задание 3
Даны координаты точек А, В, С, Д. Найдите: а) скалярное произведение векторов АВ*3ВС; б) модуль векторного произведения ВА*ДС; в) смешанное произведение векторов АВ, ВД, СА; г)проверьте, лежат ли точки А, В, С, Д в одной плоскости.
А (4, 5, 4), В(-1, -3, -2), С(-1, 5, -4), Д (2, 3, -1)
Задание 4
Используя координаты точек из контрольного задания к теме 3, найдите: а) уравнение плоскости, проходящей через точки В, С, Д; б) уравнение плоскости, проходящей через точку В, перпендикулярно прямой АД; в) уравнение плоскости, проходящей через точку Д, параллельно векторам АВ и СВ; г) сумму длин отрезков, отсекаемых плоскостью, проходящей через точки В, С, Д (пункт а) на координатных осях.
Вариант 20
Задание 1
Даны матрицы А и В. Найти: а)произведение матриц А и В; б) определитель матрицы А; в) матрицу, обратную к матрице А.
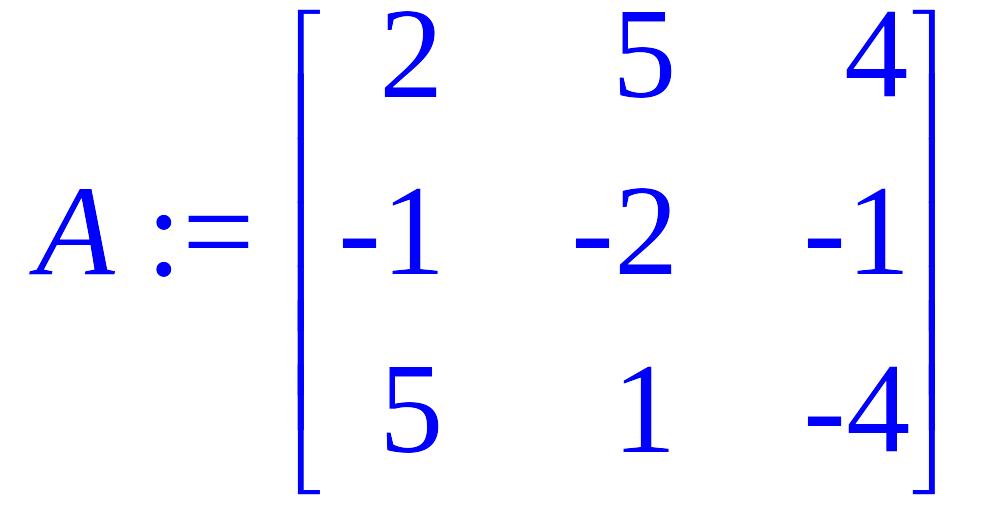

Задание 2
Решите систему линейных алгебраических уравнений а) методом обратной матрицы; б)методом Крамера; в)методом Гаусса.
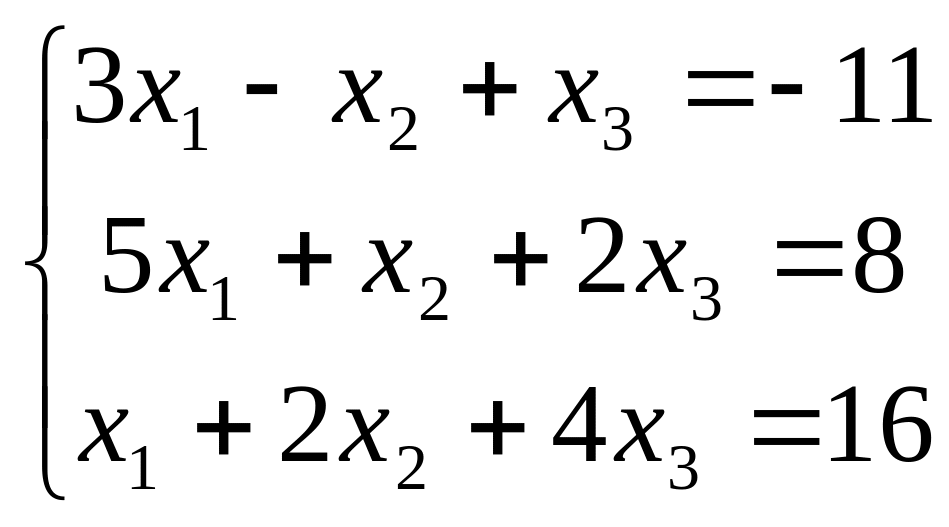
Задание 3
Даны координаты точек А, В, С, Д. Найдите: а) скалярное произведение векторов АВ*3ВС; б) модуль векторного произведения ВА*ДС; в) смешанное произведение векторов АВ, ВД, СА; г)проверьте, лежат ли точки А, В, С, Д в одной плоскости.
А (5, 1, -2), В(-2, 3, 2), С(3 ,-5,6), Д (-2, 4, -1)
Задание 4
Используя координаты точек из контрольного задания к теме 3, найдите: а) уравнение плоскости, проходящей через точки В, С, Д; б) уравнение плоскости, проходящей через точку В, перпендикулярно прямой АД; в) уравнение плоскости, проходящей через точку Д, параллельно векторам АВ и СВ; г) сумму длин отрезков, отсекаемых плоскостью, проходящей через точки В, С, Д (пункт а) на координатных осях.
