Свободный модуль Определение

Пусть   — (левый) модуль над ассоциативным кольцом   и   — подмножество в  .

Определение 1. Модуль   называется конечно порожденным¹⁾, или модулем конечного типа, если он имеет конечное числообразующих.

Определение 2. Модуль, порожденный единственным элементом  , записывается в виде  ²⁾ и называется главным модулем³⁾.

Определение 3. Множество   называется базисом⁴⁾ модуля  , если   не пусто, порождает   и линейно независимо.

Предложение 1. Если   — базис модуля  , то каждый элемент   из   единственным образом образом представляется в виде линейной комбинации элементов из  .

Определение 4. Под свободным модулем⁵⁾ понимается модуль, обладающий базисом, или же нулевой модуль.

Определение 5. Размерностью⁶⁾   свободного модуля   над кольцом   называется мощность его базиса.

Пример 1. Пусть   — ассоциативное кольцо с единицей, тогда   является конечно порожденным модулем над собой, а его базис состоит из одного элемента  . Таким образом,   — главный модуль над собой.

Пример 2. Кольцо многочленов   от одной переменной над коммутативным ассоциативным кольцом с единицей  порождено (как модуль над  ) бесконечным множеством   линейно независимым над  .

Пример3. Пусть   — непустое множество, и для каждого   пусть  , где   — ассоциативное кольцо с единицей, и все   рассматриваются как  -модули. Положим  . Модуль   обладает базисом, состоящим из элементов   в  ,  -й компонентой которых является единичный элемент из  , а все другие компоненты равны нулю.

Скалярное произведение Скалярное произведение

Определение 1. Пусть   — векторное пространство над полем   или  . Билинейная форма   называется скалярным произведением¹⁾, если выполнены условия:

1. Симметричность:   для всех  ;

2. Положительная определенность:   для всех 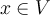 , и обращается в нуль, лишь если  .

Часто для скалярного произведения векторов   и   вместо   используют обозначение   или  .

Пример 1. На пространстве непрерывных функций   можно задать скалярное произведение  .

Пример 2. На пространстве   скалярное произведение задается формулой:  , где   и   — разложение векторов по стандартному базису  .

Евклидово пространство

Определение 2. Евклидовым векторным пространством²⁾ называется векторное пространство над полем   с фиксированным скалярным произведением  .

Пример 3. Пространство   является евклидовым пространством. Скалярное произведение здесь можно задать формулой из примера 2.

Определение 3. Пусть   — евклидово пространство. Для любого   число   называется длиной, илинормой вектора  .

Предложение 1 (Неравенство Коши-Буняковского). Для произвольных векторов   из евклидова пространства  справедливо неравенство .

Пример 4. В случае, когда евклидово пространство — это пространство непрерывных на отрезке   вещественнозначных функций³⁾, неравенство Коши-Буняковского имеет вид .

Определение 4. Векторы   из евклидова пространства   называются ортогональными⁴⁾, если  .

Теорема Лапласа Минор

Пусть   — квадратная матрица порядка   с коэффициентами из кольца  , .

Определение 1. Минором¹⁾ порядка   произвольной матрицы   называется определитель ее подматрицы порядка  .

Таким образом, чтобы найти некоторый минор порядка  , мы должны выполнить следующие действия. Зафиксируем в матрице   любые   строк с номерами   и   столбцов с номерами  . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу. Ее определитель   — это минор порядка  , который мы будем обозначать через  .

Пример 1. Рассмотрим матрицу порядка 3:  . Выберем в ней 2-ю строчку и 3-й столбец. Тогда число, стоящее на пересечении этой строчки и этого столбца,   — минор порядка 1. Всего в этой матрице 9 миноров порядка 1.

Пример 2. В матрице из примера 3 выберем 1-ю и 3-ю строки и 1-й и 2-й столбец. Соответствующий минор   будет равен  .

Определение 2. Пусть   — минор порядка   квадратной матрицы  , построенный на строках с номерами   и столбцах с номерами  . Вычеркнув из матрицы эти строки и столбцы, получим квадратную матрицу, определитель которой   будем называть дополнительным минором²⁾ к минору  . Произвольный элемент   матрицы   можно рассматривать как минор  . В этом случае   называют дополнительным минором к элементу  .

Пример 3. Дополнительный минор к минору   из примера 4 равен  .

Пример 4. Дополнительный минор к элементу   матрицы   из примера 3 равен 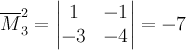 .