Бзраспис(первичное; план)

БЗРАСПИС(10;А1:А6)=30.9375.

3.5 Расчет текущей стоимости.

Во многих задачах используется понятие текущей (современной) стоимости (present value) будущих доходов и расходов.

Это понятие базируется на положении о том, что полученная в будущем сумма денег имеет меньшую стоимость, чем ее эквивалент, полученный сегодня.

Согласно концепции временной стоимости денег расходы и доходы, не относящиеся к одному моменту времени, можно сопоставить путем приведения к одному сроку (т.е. путем дисконтирования).

Текущая стоимость получается как результат приведения будущих доходов и расходов к начальному периоду времени. Excel содержит ряд функций, которые позволяют рассчитывать:

1. текущую стоимость единой суммы вклада (займа) и фиксиро­ванных периодических платежей (функция ПЗ).

2. чистую текущую стоимость будущих периодических расходов и поступлений (функция НПЗ):

3. чистую текущую стоимость будущих расходов и поступлений, которые не обязательно периодические (функция ЧИСТНЗ).

Заметим, что расчеты с использованием функций НПЗ и ПЗ являются частными случаями вычисления текущей стоимости ожидаемых доходов и расходов, которые в общем случае могут быть переменной величины и происходить в разные периоды времени.

Расчет при помощи функции ПЗ требует денежных потоков равной величины и равных интервалов между операциями.

Функция НПЗ допускает денежные потоки переменной величины через равные периоды времени.

Наиболее общий расчет можно осуществить при помощи функции ЧИСТН3, которая позволяет вычислять чистую текущую стоимость переменных денежных потоков, являющихся нерегулярными.

3.6 Функция пз

Возвращает текущий объем вклада. Функция предназначена для расчета текущей стоимости, как единой суммы вклада (займа), так и будущих фиксированных периодических платежей.

Текущий объем - это общая сумма, которую составят будущие платежи. Например, когда вы берете взаймы деньги, заимствованная сумма и есть текущий объем для заимодавца.

Этот расчет является обратным к опре­делению будущей стоимости при помощи функции БЗ. Значение, которое возвращает функция ПЗ - это аргумент pv формулы (3.1).

Синтаксис ПЗ(норма; кпер; выплата; бс; тип)

норма - это процентная ставка за период.

Например, если вы получили ссуду под автомобиль под 10 процентов годовых и делаете ежемесячные выплаты, то процентная ставка за месяц составит 10%/12, или 0,83%. В качестве значения аргумента ставка нужно ввести в формулу 10%/12 или 0,83% или 0,0083.

кпер - это общее число периодов выплат годовой ренты.

Например, если вы получили ссуду на 4 года под автомобиль и делаете ежемесячные платежи, то ваша ссуда имеет 4*12 (или 48) периодов. Вы должны ввести число 48 в формулу в качестве значения аргумента кпер.

выплата - это выплата, производимая в каждый период и не меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи и платежи по процентам, но не включают других сборов или налогов. Например, ежемесячная выплата по четырехгодичному займу в 10 000 руб. под 12 процентов годовых составит 263,33 руб. Вы должны ввести число -263,33 в формулу в качестве значения аргумента выплата.

бс - это будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если бс опущено, оно полагается равным 0 (будущая стоимость займа, например, равна 0). Например, если вы хотите накопить 50 000 руб. для оплаты специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая стоимость. Вы можете сделать предположение о сохранении заданной процентной ставки и определить, сколько нужно откладывать каждый месяц.

тип - это число 0 или 1, обозначающее, когда должна производиться выплата ( в начале – 1 или в конце –0 месяца)

Убедитесь, что вы последовательны в выборе единиц измерения для задания «ставки» и кпер. Если вы делаете ежемесячные выплаты по четырехгодичному займу под 12 процентов годовых, то используйте 12%/12 для задания аргумента норма и 4*12 для задания аргумента кпер. Если вы делаете ежегодные платежи по тому же займу, то используйте 12% для задания аргумента «ставка» и 4 для задания аргумента кпер.

В функциях, связанных с интервалами выплат, выплачиваемые Вами деньги, такие как депозит на накопление, представляются отрицательным числом; деньги, которые Вы получаете, такие как чеки на дивиденды, представляются положительным числом. Например, депозит в банк на сумму 1 000 руб. представляется аргументом -1000, если вы вкладчик и представляется аргументом 1000, если вы - банк.

Эта функция может быть полезна в следующих расчетах.

1. Д 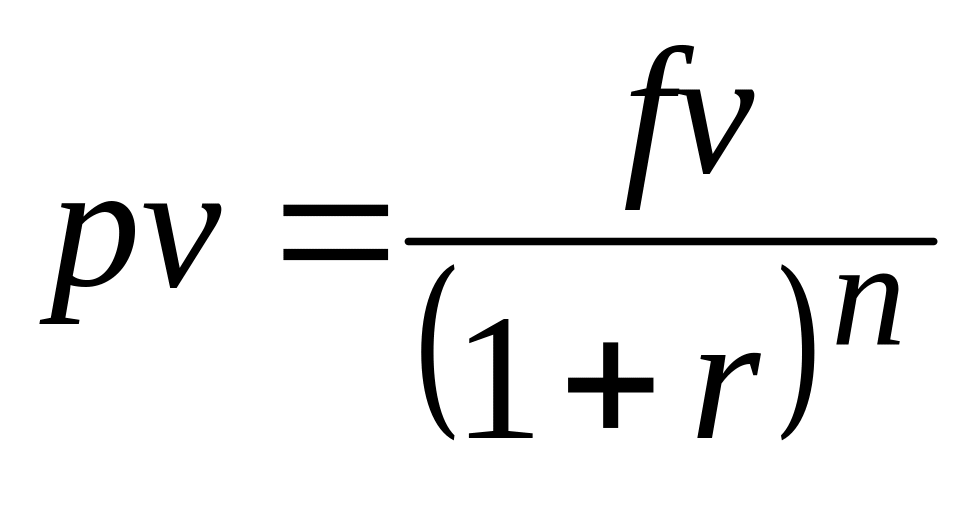опустим, известно будущее (наращенное) значение вклада (займа). Требуется определить текущее значение этого вклада, т.е. сумму, которую необходимо положить на счет сего­дня, чтобы в конце п-го периода она достигла заданного значе­ния. Это значение можно получить из формулы (3.3):

(3.7)

Расчет при использовании функции ПЗ в общем виде запишется так:

=ПЗ(норма; кпер; ;бс)

2. Предположим теперь, что требуется найти текущую стоимость будущих периодических постоянных платежей, которые производятся в начале или в конце каждого расчетного периода. Согласно концепции временной стоимости, чем дальше отстоит от настоящего момента поступление или расходование средств, тем меньшую текущую ценность оно представляет. Таким образом, при прочих равных условиях текущая стоимость вкладов пренумерандо больше, чем текущая стоимость вкладов постнумерандо.

3. Расчет текущей стоимости серии будущих постоянных периодических платежей, производимых в начале каждого периода (обязательные платежи) и дисконтированных нормой дохода r, ведется по формуле

(3.8)

pv - текущая стоимость серии фиксированных периодических платежей;

pmt - фиксированная периодическая сумма платежа:

п - общее число периодов выплат (поступлений);

r - постоянная процентная ставка.

Формула позволяет рассчитать современную стоимость постоянной ренты пренумерандо.

Для расчета этой величины функция ПЗ имеет вид