Компендиум-глоссарий

События и вероятность

Под испытанием (опытом, экспериментом) понимается выполнение определенного комплекса условий S, в которых наблюдается то или иное явление.

Событие – исход испытания. События обозначаются большими латинскими буквами А, В, С, …

Достоверное событие () – обязательно должно произойти в результате испытания.

Невозможное событие () – не может произойти в результате испытания.

События называются несовместными, если наступление одного из них исключает появление любого другого. В противном случае события называются совместными.

События называются равновозможными, если в результате испытания по условиям симметрии ни одно из них не является объективно более возможным.

Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них.

Несколько событий образуют полную группу событий, если они являются единственно возможными и несовместными исходами испытания.

Два события А и , образующих полную группу называются противоположными событиями.

Элементарными исходами (случаями, шансами) называются исходы некоторого испытания, если они образуют полную группу и являются равновозможными.

Классическое определение вероятности события

Вероятность события А равна отношению числа элементарных исходов, благоприятствующих появлению события А к общему числу элементарных исходов:

.

Свойства вероятности события:

1) . 2) . 3) .

Практически невозможным называется такое событие, вероятность которого очень мала (близка к нулю).

Практически достоверным называется такое событие, вероятность которого достаточно большая (близка к единице).

Статистической вероятностью события А называется относительная частота появления этого события в n произведенных испытаниях:

,

где m – число испытаний, в которых появилось событие А.

Геометрическое определение вероятности

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l определяется равенством:

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания этой точки на фигуру g определяется равенством:

Суммой событий А и В называется такое событие С=А+В, которое означает наступление или А, или В, т.е. хотя бы одного из них.

Произведением событий А и В называется событие С=АВ, состоящее в совместном наступлении события А и события В.

Основные теоремы

Теорема сложения вероятностей событий

Для несовместных событий:

Для произвольных событий:

Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице.

Следствие 2. Сумма вероятностей противоположных событий равна единице.

Вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В.

Два события А и В называются независимыми, если появление одного из них не меняет вероятности появления другого:

Теорема умножения вероятностей событий

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Формула полной вероятности

Если событие А может произойти только при появлении одного из событий (гипотез) Н₁, Н₂, …, H_n образующих полную группу, то

Формула Байеса

Если произошло событие А, которое может появиться только с одной из гипотез Н₁, Н₂, …, H_n образующих полную группу событий, то условные вероятности гипотез определяются по формуле:

Повторные испытания

Повторные испытания – это последовательное проведение n раз одного и того же опыта или одновременное проведение n одинаковых опытов.

Последовательностью независимых испытаний (схемой Бернулли) называют повторные испытания, удовлетворяющие следующим условиям:

1) в каждом испытании может появится только два исхода: наступит некоторое событие А (успех), либо наступит его дополнение (неудача);

2) испытания являются независимыми, т.е. вероятность успеха в m-м испытании не зависит от исходов всех испытаний до m-го;

3) вероятность успеха во всех испытаниях постоянна (вероятность неудачи в каждом испытании обозначают q: .

При рассмотрении схемы испытаний Бернулли основной задачей является нахождение вероятности – вероятность того, что в n независимых испытаниях событие А наступит точно m раз (0 ≤ m ≤ n).

Формула Бернулли

,

где , .

Число наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события , по крайней мере, не меньше вероятности других событий при любом m:

Формула Пуассона

Если число испытаний неограниченно увеличивается ( ), вероятность p наступления события А в каждом испытании неограниченно уменьшается ( ), но так, что их произведение np является постоянной величиной ( – const), то:

На практике используется приближенное равенство:

,

когда вероятность успеха мала, т.е. успех является редким событием, а количество испытаний n – велико: и .

В тех случаях, когда число испытаний n – велико, а вероятность успеха p – не близка к нулю ( ), для вычисления используют теоремы Муавра-Лапласа.

Локальная теорема Муавра-Лапласа

Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число независимых испытаний достаточно велико ( , , ), то имеет место приближенное равенство:

– функция Гаусса (плотность стандартного нормального распределения).

Приближенное равенство тем точнее, чем больше n. На практике проверяется условие:

Свойства функции Гаусса:

1) – функция четная: ;

2) при , – монотонно убывает;

3) при , (на практике считают, что при , ).

Интегральная теорема Муавра-Лапласа

Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число независимых испытаний достаточно велико ( , , ), то имеет место приближенное равенство:

где – вероятность того, что событие А в n независимых испытаниях наступит не менее  раз и не более  раз;

– функция Лапласа.

Приближенное равенство тем точнее, чем больше n. При оно дает удовлетворительное приближение.

Свойства функции Лапласа

1) – нечетная функция: ;

2) – монотонно возрастающая функция;

3) (на практике можно считать, что при , ).

Случайные величины и законы их распределений

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений.

Случайная величина называется дискретной, если ее множество значений конечное, или бесконечное, но счетное.

Случайная величина называется непрерывной, если она может принимать любые значения из некоторого промежутка.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения для дискретной случайной величины может быть задан в виде ряда распределения случайной величины – таблицы, в первой строке которой в порядке возрастания указаны возможные значения случайной величины, а во второй строке – соответствующие вероятности.

Х			…
P			…

При этом – вероятность события . Коротко закон распределения дискретной случайной величины будет записывать в виде .

Все события образуют полную группу событий поэтому

Математические операции над случайными величинами

Две случайные величины X и Y называются независимыми, если события и независимы для всех значения и .

Пусть закон распределения случайной величины Х имеет вид:

а закон распределения случайной величины Y имеет вид:

Произведением случайной величины Х на постоянную величину k называется случайная величина Z, которая принимает значения , i = 1,..,n с теми же вероятностями :

m-й степенью случайной величины Х называется случайная величина , которая принимает значения с теми же вероятностями , i = 1,..,n:

Суммой случайных величин Х и Y называется случайная величина Z=X+Y, принимающая все значения вида с вероятностями .

Разностью случайных величин Х и Y называется случайная величина Z=X–Y, принимающая все значения вида с вероятностями .

Произведением случайных величин Х и Y называется случайная величина Z=XY, принимающая все значения вида с вероятностями .

Если Х и Y – независимы, то .

Числовые характеристики дискретных случайных величин

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятности:

Свойства математического ожидания:

1. 

2. 

3. 

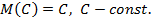
4. если Х, Y – независимы.

5. 

Дисперсией случайной величины называется математическое ожидание квадрата ее отклонений от математического ожидания:

Дисперсия может быть рассчитана по формуле:

Средним квадратическим отклонением (стандартным отклонением) случайной величины называется корень квадратный из ее дисперсии:

Свойства дисперсии:

1. 

2. 

3. если Х, Y – независимы.

Модой дискретной случайной величины называется возможное значение случайной величины, которое имеет наибольшую соответствующую вероятность.

Медианой дискретной случайной величины называется возможное значение случайной величины, слева и справа от которого в ряде распределения случайной величины одинаковое число значений случайной величины.

Интегральная и дифференциальная функции распределения случайной величины

Функцией распределения случайной величины (интегральной) называют функцию, определяющую для каждого значения х вероятность того, что случайная величина Х примет значение меньшее, чем х:

Свойства функции распределения

1. 

2. – монотонно не убывает: если , то .

3. 

4. 

Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.

Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю:

Для непрерывной случайной величины справедливо равенство:

Плотностью вероятности (дифференциальной функцией распределения) непрерывной случайной величины называется производная ее функции распределения:

Для непрерывной случайной величины справедливо равенство:

Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

Свойства дифференциальной функции распределения:

1. 

2. 

Числовые характеристики непрерывных случайных величин:

Математическое ожидание:

Дисперсия:

Равномерный закон распределения

Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a; b], если ее плотность вероятности (х) постоянна на этом отрезке и равна нулю вне его.

Плотность вероятности и функция распределения равномерно распределенной случайной величины имеют вид:

Числовые характеристики равномерно-распределенной случайной величины:

Случайная величина Х равномерно распределенная на отрезке [0; 1] называется случайным числом от 0 до 1.

Нормальный закон распределения

Непрерывная случайная величина Х имеет нормальный закон распределения, с параметрами a и , если ее плотность вероятности имеет вид:

Обозначение:

Если , то .

Функция распределения нормально распределенной случайной величины имеет вид:

Нормальное распределение с параметрами называется стандартным: .

Если , то .

Вероятность попадания нормально распределенной случайной величины на заданный участок:

Элементы математической статистики

Генеральная совокупность и выборка

Генеральная совокупность – вся подлежащая изучению совокупность наблюдений, производимых в неизменных условиях.

В математической статистике генеральная совокупность часто понимается как совокупность всех мыслимых наблюдений, которые могут быть произведены при выполнении некоторых условий.

Выборка (выборочная совокупность) – совокупность наблюдений, отобранных случайным образом из генеральной совокупности.

Число наблюдений в совокупности называется ее объемом.

N – объем генеральной совокупности.

n – объем выборки.

Выборочный метод – метод статистического исследования, состоящий в том, что на основе изучения выборки делается заключение о всей генеральной совокупности.

Если после исследования объект из выборки возвращается в генеральную совокупность, то такая выборка называется повторной (возвратной); если объект не возвращается в генеральную совокупность, то выборка называется бесповторной (безвозвратной).

Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем нас признаке генеральной совокупности.

Репрезентативность выборки обеспечивается:

- объемом выборки;

- случайностью отбора ее элементов;

- все элементы совокупность должны иметь одинаковую вероятность попадания в выборку.

Вариационный ряд

Наблюдаемые значения случайной величины х₁, х₂, …, х_k называются вариантами.

Частотой варианты х_i называется число n_i (i=1,…,k), показывающее, сколько раз эта варианта встречается в выборке.

Частостью (относительной частотой, долей) варианты х_i (i=1,…,k) называется отношение ее частоты n_i к объему выборки n.

Частоты и частости называют весами.

Накопленной частотой называется количество вариант, значения которых меньше данного х:

Накопленной частостью называется отношение накопленной частоты к объему выборки:

Вариационным рядом (статистическим рядом) – называется последовательность вариант, записанных в порядке возрастания и соответствующих им весов.

Вариационный ряд может быть дискретным (выборка значений дискретной случайной величины) и непрерывным (интервальным) (выборка значений непрерывной случайной величины).

Дискретный вариационный ряд имеет вид:

Значение изучаемого свойства X хi	х1	…	хi	…	xk
Частота значения хi ni	n1	…	ni	…	nk

Когда число вариант велико или признак является непрерывным (случайная величина может принимать любые значения в некотором интервале), составляют интервальный вариационный ряд.

Для построения интервального вариационного ряда проводят группировку вариант – их разбивают на отдельные интервалы:

Число интервалов иногда определяют с помощью формулы Стерджеса:

Затем подсчитывается число вариант, попавших в каждый интервал – частоты n_i (или частости n_i/n). Если варианта находится на границе интервала, то ее присоединяют к правому интервалу.

Интервальный вариационный ряд имеет вид:

Интервалы значений изучаемого свойства X [хi, хi+1)	[х1; х2)	…	[хi,;хi+1)	…	[хk-1; хk)
Относительная частота ni	n1	…	ni	…	nk

Эмпирической (статистической) функцией распределения называется функция, значение которой в точке х равно относительной частоте того, что варианта примет значение, меньшее х (накопительной частости для х):

Полигоном частот называют ломанную, отрезки которой соединяют точки с координатами (х₁; n₁), (х₂; n₂), …, (х_k; n_k). Аналогично строится полигон частостей, который является статистическим аналогом многоугольника распределений.

Для непрерывного вариационного ряда полигон можно построить, если в качестве значений х₁, х₂, …, х_k взять середины интервалов.

Интервальный вариационный ряд графически обычно изображают с помощью гистограммы.

Гистограмма – ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы длины h = x_i+1 – x_i, i = 0,…,k-1, а высоты равны частотам (или частостям) интервалов n_i (w_i).

Кумулята (кумулятивная кривая) – кривая накопленных частот (частостей). Для дискретного ряда кумулята представляет ломанную, соединяющую точки или , . Для интервального ряда кумулята начинается с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте (частости), равной нулю. Другие точки этой ломанной соответствуют концам интервалов.

Числовые характеристики вариационных рядов

Выборочное среднее

где – варианты дискретного ряда или середины интервалов интервального ряда;

– частоты вариант или интервалов;

– частости вариант или интервалов.

Средняя отклонений вариантов от средней равна нулю:

Медианой (Md) вариационного ряда называется значение признака, приходящегося на середину ранжированного ряда наблюдений.

Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов.

Для интервального вариационного ряда:

Модой (Mo) вариационного ряда называется варианта, которой соответствует наибольшая частота.

Для дискретного вариационного ряда мода находится по определению.

Для интервального вариационного ряда:

Абсолютные показатели вариации

Размах (R) – разность между наибольшим и наименьшим вариантами ряда:

Среднее линейное отклонение (d) – средняя арифметическая абсолютных величин отклонений вариантов от их средней:

Выборочная дисперсия ( ) – среднее арифметическое квадратов отклонений вариант от их выборочной средней:

где – варианты дискретного ряда или середины интервалов интервального ряда.

Для практических вычислений более удобной является формула:

Среднее квадратическое отклонение (стандартное отклонение):

Относительные показатели вариации

Коэффициент осцилляции:

Относительное линейное отклонение:

Коэффициент вариации:

Оценка параметров

Оценкой параметра называется всякая функция результатов наблюдений над случайной величиной Х, с помощью которой судят о значении параметра .

Оценка параметра называется несмещенной (смещенной), если ее математическое ожидание равно (не равно) оцениваемому параметру:

Оценка параметра называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:

Оценка параметра называется эффективной, если она имеет наименьшую дисперсию из всех несмещенных оценок параметра , вычисленных по выборкам одного объема n.

Выборочная средняя является несмещенной оценкой генеральной средней.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии (она занижает генеральную дисперсию). Поэтому на практике часто используют исправленную выборочную дисперсию, которая является несмещенной и состоятельной оценкой генеральной дисперсии:

и исправленное среднее квадратическое отклонение:

Интервальные оценки параметров

Доверительным интервалом (интервальной оценкой) для параметра с надежностью оценки  называется числовой промежуток , содержащий истинное значение данного параметра с вероятностью, равной :

где – оценка неизвестного параметра (например, точечная оценка), – некоторое число.

Как правило, надежность оценки  – число, близкое к единице. Число называется уровнем значимости.

Интервальной оценкой (с надежностью ) математического ожидания a нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении  генеральной совокупности служит доверительный интервал

где – точность оценки, n – объем выборки, t – значение аргумента функции Лапласа (t), при котором ;

При неизвестном  (и объеме выборки n < 30):

где S – исправленное выборочное среднее квадратическое отклонение, – находят по таблице значений по заданным n и .

Интервальной оценкой (с надежностью ) среднего квадратического отклонения  нормально распределенного количественного признака Х по исправленному выборочному среднему квадратическому отклонению S служит доверительный интервал:

.

Проверка статистических гипотез

Статистической гипотезой называется любое предположение о виде или параметре неизвестного закона распределения.

Проверяемую гипотезу обычно называют нулевой и обозначают . Наряду с нулевой гипотезой рассматривают альтернативную (конкурирующую) гипотезу , являющуюся логическим отрицанием .

Статистическим критерием (тестом) называется правило, по которому гипотеза отвергается или принимается.

Схема проверки статистических гипотез

1. Для основной гипотезы формулируется альтернативная гипотеза .

2. Выбирается малое положительное число  – уровень значимости проверки. Обычно  принимается в пределах от 0,01 до 0,05.

3. Вводится специально составленная выборочная характеристика (статистика, критерий) T, значение которой можно получить по выборке, о которой известно точное или приближенное распределение.

4. По известному распределению величины T определяется область :

т.е. если , то принимается.

При этом возможно: ; .

Значения и называются критическими и обозначаются .

Область D называется областью принятия гипотезы (областью допустимых значений), а остальная часть числовой прямой – областью отклонения гипотезы (критической областью).

5. По данной выборке вычисляется наблюдаемое (фактическое) значение критерия (статистики) и выполняется проверка условия . Если это условие выполняется, то гипотеза принимается – она не противоречит опытным данным. В противном случае гипотеза отклоняется и принимается альтернативная гипотеза .

Возможны четыре случая:

Гипотеза	Принимается	Отвергается
Верна	Правильное решение	Ошибка 1-го рода
Не верна	Ошибка 1-го рода	Правильное решение

Вероятность  – вероятность отвергнуть верную гипотезу (вероятность совершить ошибку 1-го рода) называется уровнем значимости критерия.

Вероятность – не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу , когда она не верна, называется мощностью критерия.

Критическая область должна быть такой, чтобы при заданном уровне значимости  мощность критерия была максимальной.

104