VIII. Содержание различных видов контроля по дисциплине
1. Примерные темы контрольных работ Вариант 1
1. Доказать равенство и проиллюстрировать диаграммой Эйлера-Венна:
=
2. Найти значение выражения:
| x – 5 – |x–3 | |
3. Используя свойства пределов функций, найти пределы:
4. Найти производные функций y(x):
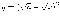
5.
Вычислить интеграл:
6. Вычислить площадь фигуры, ограниченной параболой y=2x – x2 и прямой y=x .
7. Найдите произведение матриц AB, если
,
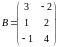
8. Найти определитель матрицы А:
А=
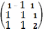
9. Решите систему линейных уравнений:
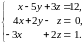
10. Найдите вероятность того, что событие А появится не менее двух раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,6.
Вариант 2
1. Доказать равенство и проиллюстрировать диаграммой Эйлера-Венна:
2. Функция y=f(x) задана таблицей:
-
x
5,2
5,4
5,6
y
2,45
2,6
2,95
Используя линейное интерполирование найти:
а) f(5,45); б) x, если f(x)=2,5.
3. Используя свойства пределов функций, найти пределы:
4. Найти производные функций y(x):
5.
Вычислить интеграл:
6. Вычислить объем тела, полученного от вращения вокруг оси ординат плоской фигуры, ограниченной линиями y= x2 и y=x4 .
7. Найти произведение матриц АВ, если
А=
В
= 
8. Найти матрицу А-1, обратную к матрице А:
А=
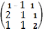
9. Решить систему линейных уравнений:
10. Случайная величина распределена по нормальному закону. Среднеквадратичное отклонение и выборочное среднее этой случайной величины равны 3 и 4, соответственно. Найти доверительный интервал для оценки неизвестного математического ожидания, если объем выборки равен 36, а надежность оценки должна равняться 95%.
2. Примерные вопросы экзамена
Понятие множества, операции над множествами и их свойства.
Числовые множества, числовая ось, сегмент, интервал.
Модуль числа, ε-окрестность точки на числовой оси.
Понятие функции, области определения и значений функции.
Основные элементарные функции и их свойства.
Обратная и сложная функции.
Алгебраические и трансцендентные функции.
Основные приемы построения графиков функций.
Линейное интерполирование функции (прямое и обратное).
Числовая последовательность и ее предел.
Предел функции в бесконечности и в точке.
Основные теоремы о пределах. Признаки существования предела.
Замечательные пределы.
Бесконечно малые и бесконечно большие величины.
Непрерывность функций.
Определение производной, схема вычисления производной.
Геометрический, механический смысл производной.
Основные правила дифференцирования.
Производные основных элементарных функций.
Производная сложной и обратной функций.
Производные высших порядков.
Теорема Ферма об экстремуме функции.
Правило Лопиталя.
Экстремумы функций и условия их существования.
Выпуклость функций. Точки перегиба.
Асимптоты графика функции. Нахождение асимптот.
Схема исследования функций и построения графиков.
Понятие дифференциала функции и его применение.
Неопределенный интеграл и его свойства.
Неопределенные интегралы основных элементарных функций.
Методы интегрирования функций.
Определенный интеграл и его свойства.
Формула Ньютона-Лейбница.
Вычисление площади геометрических фигур, объемов тел вращения.
Дифференциальные уравнения первого порядка.
Задача Коши.
Качественный анализ дифференциальных уравнений.
Однородные дифференциальные уравнения.
Дифференциальные уравнения второго порядка.
Длина вектора, действия с векторами.
Скалярное произведение векторов. Угол между векторами.
Квадратичные формы.
Квадратные матрицы и их определители.
Миноры и алгебраические дополнения.
Определители матриц и их свойства.
Обратная матрица и ранг матрицы.
Методы решения систем линейных уравнений.
Классическое определение вероятности.
Вычисление вероятности с помощью формул комбинаторики.
Вероятность несовместных и противоположных событий.
Вероятность совместных событий.
Условная вероятность.
Формула полной вероятности.
Биномиальное распределение вероятностей.
Нормальное распределение вероятностей.
Выборочные совокупности, варианты, частоты, объем выборки.
Эмпирические функции распределения, полигон и гистограмма
Математическое ожидание и дисперсия.
Оценка генеральной дисперсии по исправленной выборочной.
Точность оценки, доверительный интервал и доверительная вероятность.