Звіт повинен містити

1. Тему та мету роботи.

2.Передаточну функцію ланки, що вивчається та значення коефіцієнтів підсилення і постійних часу згідно варіанту.

3.Розраховані залежності, які необхідні для побудови частотних та часових характеристик.

4.Графіки усіх отриманих характеристик.

5. Висновки по роботі

Варіанти завдань

№ варіанту	K	T	№ варіанту	K	T
1	4	1	16	6	0,5
2	2	0,1	17	0,5	0,1
3	3	1	18	4	0,8
4	5	0,25	19	1,5	0,25
5	1	0,5	20	3	0,5
6	4	0,3	21	2	1
7	1	0,5	22	2	0,1
8	3	1	23	4,2	0,6
9	5	0,4	24	1	0,7
10	2	1	25	2,5	0,2
11	1	0,25	26	0,5	1
12	7	1	27	4	0,6
13	3	1	28	4	1
14	0,5	0,25	29	2	0,5
15	2,5	0,7	30	3	1

Лабораторна робота №3

Тема: реальна інтегруюча ланка

Мета: зняти часові та частотні характеристики, виконати аналіз реальної інтегруючої ланки.

Теоретичні відомості

Передаточна функція має вигляд:

Диференційне рівняння ланки:

Легко бачити, що ланка з даною передаточною функцією може розглядатися як послідовне з’єднання двох елементарних ланок: ідеального інтегруючого з передаточною функцією 1/р і аперіодичної ланки з передаточною функцією к/(Тр+1).

Із взаємної відповідності динамічних характеристик відомо, що перехідна функція може бути знайдена як зворотне перетворення Лапласа частки, діленим якої є передаточна функція, а дільником – оператор р. Тобто:

Знайдемо перехідну функцію. Для цього отриманий дріб розкладемо методом невизначених коефіцієнтів на прості дроби:

З таблиці зворотного перетворення Лапласа видно, що

, ,

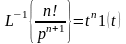Перетворивши отриману формулу, знаходимо h(t):

, або

Застосувавши методи аналітичної геометрії, можна впевнитися в тому, що асимптота до кривої відтинає на осі часу відрізок, що дорівнює постійній часу .

Коефіцієнт нахилу асимптоти:

,

а параметр, що визначає точку перетину з віссю ординат

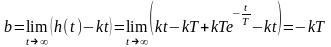
Маємо рівняння асимптоти:

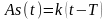
Знайдемо тепер імпульсну перехідну функцію. Як відомо, вона представляє собою похідну від перехідної функції, тобто:

Характерним є те, що дотична до графіка імпульсної перехідної функції в точці перетинає пряму паралельну осі часу на відстані від осі ординат.

Амплітудно-фазова характеристика може бути отримана шляхом підстановки в передаточну функцію .

Звідси видно, що дійсна і уявна частотні характеристики дорівнюють відповідно: ; .

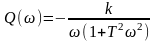Амплітудно-частотна характеристика представляє собою модуль вектора амплітудно-фазової характеристики і знаходиться за формулою:

Підставивши в дану формулу вирази для та , отримаємо:

Проаналізувавши графік функції , можна побачити, що реально інтегруюча ланка має властивості фільтру низьких частот, тобто гармонічні сигнали малої частоти пропускаються ланкою добре, а сигнали великої частоти зазнають сильного ослаблення.

Фазочастотна характеристика може бути отримана за формулою:

В ФЧХ маємо доданок 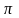завдяки тому, що комплексне число знаходиться на комплексній площині в 3 квадранті.

Чим менша частота вхідного сигналу, тим більше відставання по фазі вихідного сигналу по відношенню до вхідного. Максимально можливе відставання .

Логарифмічна амплітудно-частотна характеристика описується виразом:

Асимптотична логарифмічна амплітудно-частотна характеристика характеризується тим, що її перша асимптота при ( ) представляє пряму, що йде під нахилом :

,

а при ( ) представляє пряму, яка має нахил :

,

частота спряження при цьом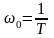у: , або на графіку .
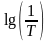