Лабораторна робота №2
Тема: реальна диференцююча ланка
Мета: зняти часові та частотні характеристики, виконати аналіз реальної диференцюючої ланки.
Теоретичні відомості
Передаточна функція
має вигляд:
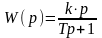
Диференційне
рівняння ланки:
Реальна диференцююча ланка – це є послідовне з’єднання ідеального диференцюючої ланки та інерційної ланки першого порядку.
Із взаємної відповідності динамічних характеристик відомо, що перехідна функція може бути знайдена як зворотне перетворення Лапласа частки, діленим якої є передаточна функція, а дільником – оператор р. Тобто:
Знайдемо перехідну функцію. Для цього отриманий дріб розкладемо методом невизначених коефіцієнтів на прості дроби:
З таблиці зворотного перетворення Лапласа видно, що
Перетворивши отриману формулу, знаходимо h(t):
,
або
Дотична до кривої
в точці
відтинає на осі часу відрізок, що дорівнює
постійній часу
.
Знайдемо тепер імпульсну перехідну функцію. Як відомо, вона представляє собою похідну від перехідної функції, тобто:
Аналогічно, можна
довести, що дотична до кривої
в точці
відтинає на осі часу відрізок, що дорівнює
постійній часу
.
Амплітудно-фазова характеристика може бути отримана шляхом підстановки в передаточну функцію .
Звідси видно, що дійсна і уявна частотні характеристики дорівнюють відповідно:
;
Амплітудно-фазова
характеристика має вигляд півкола, із
центром на дійсній осі в точці
.
Для доведення цього, піднесемо до
квадрату обидва вирази та складемо їх:
Звідси доповнивши до квадрату, отримаємо рівняння кола:
Радіус дорівнює
,
а центр знаходиться в точці
.
Амплітудно-частотна характеристика представляє собою модуль вектора амплітудно-фазової характеристики і знаходиться за формулою:
Підставивши в дану формулу вирази для та , одержимо:
Як бачимо при
маємо горизонтальну асимптоту до графіка
функції АЧХ:
.
Фазочастотна характеристика може бути отримана за формулою:
Чим більша частота
вхідного сигналу, тим менше випередження
по фазі вихідного сигналу по відношенню
до вхідного. При частоті спряження
вихідний сигнал випереджує вхідний на
.
Логарифмічна амплітудно-частотна характеристика описується виразом:
Асимптотична
логарифмічна амплітудно-частотна
характеристика характеризується тим,
що її перша асимптота при
(
)
представляє пряму, яка має нахил
:
,
а при ( ) представляє паралельну осі декад пряму:
Методичні вказівки
Робота виконується за допомогою прикладних математичних пакетів MatLab або MathCad аналогічно до попередьої роботи.
Порядок виконання роботи
1. Набрати модель системи з параметрами згідно варіанту або задати аналітичні вирази.
2. Подати на вхід одиничну ступінчату функцію та одержати графіки перехідної та імпульсної характеристики (часові) та частотних характеристик, а саме: амплітудно-частотну(АЧХ), фазо-частотну(ФЧХ), амплітудно-фазову(АФХ), логарифмічну амплітудно-частотну(ЛАЧХ) та асимптотичну логарифмічну амплітудно-частотну(АЛАЧХ).
3. Побудувати перехідну характеристику при збільшенні та зменшенні постійної часу T та коефіцієнта підсилення k у 2 рази.
4. Проаналізувати отримані результати.