Лабораторна робота №7

Тема: дослідження стійкості системи автоматичного керування

Мета: дослідити систему автоматичного керування на стійкість та визначити похибку системи за завданням та збуренням.

Теоретичні відомості

Стійкість автоматичної системи – це властивість системи повертатися у початковий (або близький до нього) стан рівноваги після припинення дії факторів, які вивели системи з цього стану.

Якщо система є стійкою, вона протидіє зовнішнім силам, а після виведення зі стану початкової рівноваги вона з певною точністю повертається в нього.

Якщо система є нестійкою, вона не повертається в стан рівноваги, при цьому вона або віддаляється від нього, або здійснює навколо нього неприпустимо великі коливання

Частотні критерії стійкості дозволяють оцінювати стійкість САК за виглядом їх частотних характеристик. Ці критерії є графоаналітичними і отримали широке застосування, оскільки дозволяють достатньо легко досліджувати стійкість систем високого порядку, а також мають достатньо просту геометричну інтерпретацію та наочність.

Методичні вказівки

Графоаналітичний метод Михайлова

Якщо підставити в характеристичний поліном чисто уявне число , то отримаємо комплексний поліном

,

де

,

.

При зміненні частоти  вектор D(j), змінюючись за величиною і напрямком, буде описувати в комплексній площині деяку криву, яка називається годографом Михайлова.

Лінійна система автоматичного керування n-порядку буде стійкою, якщо крива (годограф) Михайлова при зміненні частоти  від 0 до , починаючись на дійсній додатній піввісі, охоплює початок координат і послідовно тільки проти часової стрілки обходить n квадрантів координатної площини.

Частотний критерій Найквіста

Основне формулювання критерію Найквіста є справедливим для систем, які в розімкненому стані є стійкими:

Система автоматичного керування є стійкою, якщо амплітудно-фазова характеристика W_р(j) розімкненого контуру не охоплює точку з координатами (-1, j0).

Для судження про стійкість систем, які мають АФХ складної форми, коли характеристика перетинає дійсну вісь лівіше точки (-1, j0) декілька разів, можна використовувати правило переходів, сформульоване Я.З.  Ципкіним:

АФХ не охоплює точку (-1, j0), тобто система є стійкою, якщо при зростанні  різниця між кількістю додатних (зверху вниз) та від’ємних (знизу вверх) переходів АФХ через вісь абсцис зліва від точки (-1, j0) дорівнює нулю.

Частота, при якій амплітудна характеристика A() (модуль функції W(j)) приймає значення 1, називають частотою зрізу та позначають _зр. Частота, при якій фазовий зсув () = –, позначають _.

Порядок виконання роботи

На рисунку наведено структурну схему тиристорного електропривода постійного струму, де 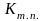– коефіцієнт підсилення тиристорного перетворювача за напругою; – еквівалентна стала часу тиристорного перетворювача; – активний опір силового кола; с – стала двигуна (добуток конструктивної сталої на номінальний магнітний потік); 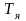– електромагнітна стала силового кола; – електромеханічна стала електропривода; , – коефіцієнти зворотних зв’язків за струмом та швидкістю відповідно.

1. Для наведеної системи автоматичного керування при заданих параметрах визначити, чи є вихідна система (без використання регуляторів) стійкою. Для непарних варіантів дослідження стійкості виконати за критерієм Михайлова, для парних – за критерієм Найквіста.

2. Визначити запаси стійкості за амплітудою та за фазою.

3. Дослідити систему на стійкість при використанні пропорційно-інтегрального регулятору струму

, ,

та пропорційного регулятора швидкості

.

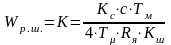Визначити запаси стійкості за амплітудою та за фазою.

4. Визначити усталене значення похибки системи за завданням та збуренням для вихідної та скорегованої (з регуляторами) системи.