Математическая формулировка общей задачи линейного программирования

Для математической формулировки задач линейного программирования в общем виде применяются условные общепринятые обозначения:

n – количество переменных;

m – количество ограничений;

x_j – неизвестные искомые переменные величины;

j – номер переменной, изменяющийся от 1 до n (j = 1, 2, …, n);

a_ij – коэффициенты при неизвестных величинах;

i – номер ограничения, изменяющийся от 1 до m (i = 1, 2, …, m);

b_i – свободные члены уравнений и неравенств (заданные постоянные величины);

Z – целевая функция;

c_j – коэффициенты при искомых переменных в целевой функции.

Тогда общую задачу линейного программирования можно математически сформулировать следующим образом:

Найти такое решение Х, то есть значения неизвестных x_j (j = 1, 2, …, n), которое бы обеспечивало экстремальное значение критерия оптимальности, выраженного линейной функцией:

Z (Х) = c₁x₁ + c₂x₂ + …+ c_nx_n  extr,

при соблюдении следующих m условий (линейных ограничений):

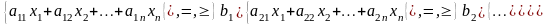
и условий неотрицательности переменных (обязательных ограничений):

x₁ 0, x₂ 0, …, x_n 0.

Структурная форма записи задачи линейного программирования

Общую задачу линейного программирования можно записать в сжатой форме с помощью знака суммирования.

Найти экстремум функции: 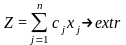, при условиях:

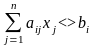i = 1, 2, …, m);

x_j 0 (j = 1, 2, …, n).

Таким образом, в математической модели задачи линейного программирования выделяют три составные части:

• целевая функция;

• система ограничений;

• условие неотрицательности искомых переменных величин.

Вопросы

1. Что такое линейное программирование?

2. Сформулируйте общую задачу линейного программирования.

3. Из каких частей состоит математическая модель задачи линейного программирования?

4. Запишите основные части математической модели задачи линейного программирования в общей и структурной формах.

3.2 Формы записи задачи линейного программирования

Существуют несколько форм записи задачи линейного программирования:

• общая (когда ограничения любого типа);

• каноническая (когда тип всех ограничений «=»);

• стандартная (когда тип ограничений либо «», либо «»).

Переход от одной формы записи задачи линейного программирования к другой называется эквивалентным преобразованием. Выполнить эквивалентные преобразования означает перейти от общей формы к стандартной и от общей перейти к канонической.

Чтобы перейти к каноническому виду задачи линейного программирования необходимо ввести в левую часть ограничения дополнительные переменные:

• если тип ограничения «», то дополнительная переменная вводится со знаком «+»,

• если тип ограничения «», то дополнительная переменная вводится со знаком «-».

Чтобы перейти к стандартному виду задачи следует умножить обе части отличающегося неравенства на –1 и соответственно изменить знак этого неравенства на противоположный («» на «» или наоборот).

Задача 1. Фермерское хозяйство занимается возделыванием двух культур (зерновых и картофеля) и располагает следующими ресурсами: земля 500 га, трудовые ресурсы – 30000 чел.-ч., механизированные ресурсы – 2800 маш. смен. Нормы затрат и выхода продукции возделывания культур представлены в таблице 1. Производство зерновых должно составлять не менее 5000 ц. Цель производства – получение максимальной прибыли, ден. ед.

Таблица 1