7.3 Основные свойства двойственных оценок

Первое свойство – дефицитность ресурсов (продукции). О дефицитности ресурсов (продукции) судят по двойственным оценкам дополнительных переменных:

• если двойственная оценка дополнительной переменной равна 0, следовательно, ресурс (продукт) не дефицитен и зачастую бывает в избытке;

• если двойственная оценка дополнительной переменной неравна 0, следовательно, ресурс (продукт) дефицитен.

Чем выше двойственная оценка, тем дефицитнее ресурс.

Использование данного свойства двойственных оценок позволяет выявить факторы, сдерживающие рост производства; помогает выбрать правильное решение, если предполагается расширение производства и требуется привлечение дополнительных ресурсов.

Рассмотрим первое свойство двойственных оценок на примере задачи 9. В данном случае используются три вида ресурсов (S₁, S₂, S₃) и производится один продукт S₄. Двойственные оценки переменных S₂ и S₄ равны 0, следовательно, трудовые ресурсы и производство зерна не дефицитны. В оптимальном решении недоиспользованные трудовые ресурсы составляют 750 чел.-ч., сверхплановое производство зерна – 24000 ц. Двойственные оценки переменных S₁ и S₃ равны соответственно 55,56 и 88,89 ден. ед., следовательно, пашня и механизированные ресурсы дефицитны.

Двойственная оценка дополнительной переменной – это оценка единицы ресурса в денежных единицах Оценка 1 га пашни составляет 55,56 ден. ед. Оценка 1 чел.-ч. равна 0. Оценка 1 машин.-смены – 88,89 ден. ед.

Второе свойство связано с мерой влияния ограничений на целевую функцию. Экономическое содержание двойственных оценок определяется содержанием критерия оптимальности и того фактора производства или условия выпуска продукции, которые оценивают.

Единицы измерения двойственных оценок и целевой функции совпадают.

Нулевые двойственные оценки по ресурсам или продукту свидетельствуют о том, что изменение объема ограничения (наличие ресурсов или плана по зерновым) на единицу не повлияет на значение целевой функции, так как ресурс по оптимальному плану имеется в избытке.

Не нулевые двойственные оценки показывают насколько увеличится или уменьшится значение целевой функции при увеличении и уменьшении ограничения (ресурса) на единицу.

По продуктам действие двойственных оценок обратное: увеличение объема производства приводит к уменьшению значения целевой функции, а уменьшение – к увеличению.

В рассматриваемой нами задаче по трудовым ресурсам двойственная оценка нулевая, следовательно, увеличение или уменьшение трудовых ресурсов на 1 чел.-ч. не повлияет на значение целевой функции.

Двойственные оценки по пашне и механизированным ресурсам – ненулевые, следовательно, увеличение или уменьшение пашни на 1 га, а механизированных ресурсов на 1 маш.–смену приведет к изменению целевой функции соответственно на 55,56 ден. ед. и 88, 89 ден. ед. Увеличение ресурсов на 1 единицу и более, выгодно, так как увеличивается значение целевой функции. Уменьшение значения не выгодно, так как значение целевой функции уменьшится.

Например, если изменить площадь пашни на 1 га, то значение целевой функции изменится следующим образом:

при увеличении площади пашни на 1 га (вместо 2200 га площадь будет равна 2001 га), тогда Z = 300000 + 55,56 = 300055,56 ден. ед.;

при уменьшении площади пашни на 1 га (вместо 2200 га площадь будет равна 1999 га), тогда Z = 300000 – 55,56 = 299944,44 ден. ед.

Самый дефицитный ресурс – механизированный, поэтому дополнительное привлечение его целесообразно, если связанные с этим затраты на единицу ресурса меньше оценки этого ресурса по оптимальному плану.

Третье свойство относится к взаимозаменяемости ресурсов или продукции. Изменяется не абсолютная взаимозаменяемость, а относительная, то есть по влиянию на значение критерия оптимальности.

Взаимозаменяемость определяется по соотношению двойственных оценок.

Например, среди двух дефицитных ресурсов в задаче наиболее дефицитен механизированный труд, найдем соотношения двойственных оценок:

и .

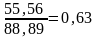Следовательно, одну маш.-смену можно заменить 1,6 га пашни, то есть одна маш.-смена дает такое же дополнительное количество валовой продукции как 1,6 га пашни. Один гектар пашни дает такое количество валовой продукции как 0,63 маш.-смен. Величины 1,6 и 0,63 являются коэффициентами взаимозаменяемости ресурсов.

Четвертое свойство. Рентабельность способов производства. Это свойство позволяет оценить эффективность производства и наметить пути совершенствования технологии производства не вошедших в оптимальный план переменных.

Если двойственная оценка основной переменной равна 0, то способ производства рентабелен, если не равна 0, то способ нерентабелен. Двойственная оценка нерентабельных способов производства указывает степень невыгодности возделывания данной культуры.

Получив оптимальное решение, определили, что выгодным является производство зерновых и сахарной свеклы (так как х₁ и х₂ вошли в базис). Нерентабельными способами являются возделывание однолетних и многолетних трав (так как х₃ и х₄ не вошли в базис). Определим рентабельность способов производства по двойственным оценкам основных переменных (х₁, х₂, х₃, х₄).

В нашей задаче двойственные оценки переменных х₁ и х₂ равны 0, следовательно, возделывание зерновых и сахарной свеклы рентабельно. Двойственные оценки х₃ и х₄ не равны 0 (11,44 и 20,22), тогда возделывание однолетних и многолетних трав нерентабельно.

Например, возделывание зерновых – рентабельно. Затраты на возделывание зерновых составляют:

Ресурсы	Оценки
пашня (1 га)	55,56 ден. ед.
трудовые ресурсы (75 чел.-ч.)	0 ден. ед.
механизированные ресурсы (0,5 маш.-смен.)	88,89 ден. ед.

Затраты и оценки всех видов ресурсов на возделывание 1 га зерновых составит 1×55,56 + 75×0 + 0,5×88,89 = 100,005 ≈ 100 ден. ед., а выход валовой продукции с 1 га зерновых составляет 100 ден. ед. Следовательно, затраты ресурсов в оценках оптимального плана равны запланированному эффекту, тогда возделывание зерновых рентабельно.

Рассмотрим, почему не выгодно возделывание однолетних трав. Затраты и оценки ресурсов на возделывание однолетних трав соответственно равны:

Ресурсы	Оценки
пашня (1 га)	55,56 ден. ед.
трудовые ресурсы (20 чел.–ч.)	0 ден. ед.
механизированные ресурсы (0,1 маш.-смен.)	88,89 ден. ед.

Следовательно, затраты всех ресурсов в ден. ед. на 1 га однолетних трав составляют 1×55,56 + 20×0 + 0,1×88,89 = 64,44 ден. ед., а выход валовой продукции с 1 га пашни по условию задачи составляет 53 ден. ед.

Рассчитаем степень невыгодности возделывания однолетних трав: 64,45 – 53 = 11,44 ден. ед. Двойственная оценка так же равна 11,44 ден. ед.

Аналогично проводится анализ по многолетним травам. Рентабельными они станут, если затраты уменьшатся на 20,22 ден. ед. и более.

Однолетние и многолетние травы не вошли в оптимальное решение, поэтому технология их производства требует усовершенствования. В рассматриваемой задаче это возможно за счет снижения затрат на производство и повышения урожайности, что повысит результаты производства, то есть количество валового продукта.

Пятое свойство связано с определением оптимальности решения. План оптимален, если выполняется равенство максимума целевой функции прямой задачи и минимума целевой функции двойственной задачи. В экономическом смысле это означает, что полученный эффект равен суммарной оценке всех затрачиваемых ресурсов.

Рассмотрим это свойство применительно к нашей задаче. Рассчитаем значение целевой функции для прямой и двойственной задач:

Z _{max пр. задачи}= 100× 2000+ 500×200 + 53×0 + 62×0 = 300000 (ден. ед.);

Z _{min дв. задачи}= 2200×55,56 + 650750×0 + 2000×88,89 – 16000×0 ≈ 300000 (ден. ед.),

так как они равны полученное решение оптимальное.

С позиции оценки затрачиваемых ресурсов оправдано производство только зерновых и сахарной свеклы.

Шестое свойство. Устойчивость двойственных оценок (основное).

Если бы двойственные оценки были не устойчивы, то есть изменялись с изменением каждого параметра задачи (объема ресурсов, объема производства продукции, количества валового продукта с 1 га), то они не представляли бы экономического интереса и потеряли бы свое значение как средства экономико-математического анализа.

Например, если изменим площадь пашни или количество механизированных ресурсов, то оптимальное решение станет другим, но двойственные оценки останутся прежними.

Изменение параметров нельзя проводит до бесконечности, на каком-то этапе это станет невыгодным, поэтому изменение параметров (корректировку) можно проводить лишь в определенных пределах (границах). При выходе за эти границы двойственные оценки меняются и экономической ценности не представляют.

Таким образом, свойство двойственных оценок оставаться устойчивыми к изменению в определенных пределах отдельных исходных параметров задачи позволяет использовать их при анализе оптимальных решений с целью обоснования, применимости и надежности рассчитанных планов.