7.2 Прямая и двойственная задача

Решение задачи симплексным методом предполагает расчет оптимального плана, в этом случае такую исходную задачу называют прямой задачей. Одновременно с решением прямой задачи решается двойственная задача.

Двойственная задача – это вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий (прямой) задачи. В двойственной задаче выполняется расчет оптимальных двойственных оценок.

Запишем прямую и двойственную задачу, используя обозначения со страницы 23.

Прямая задача (в стандартной форме): Найти такое решение Х, то есть значения неизвестных x_j (j = 1, 2,…, n), которое бы обеспечивало экстремальное значение критерия оптимальности, выраженного линейной функцией:

Z (Х) = c₁x₁ + c₂x₂ + …+ c_nx_n  extr,

при соблюдении m условий (линейных ограничений):

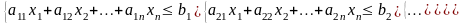
и условий неотрицательности переменных (обязательных ограничений):

x₁ 0, x₂ 0, …, x_n 0.

Двойственная задача: Найти такое решение Y, то есть значения неизвестных у_i (i = 1, 2,…, m), которое бы обеспечивало экстремальное значение критерия оптимальности, выраженного линейной функцией:

Z (Y) = b₁y₁ + b₂y₂ + …+ b_my_m  extr,

при соблюдении n условий (линейных ограничений):

и условий неотрицательности переменных (обязательных ограничений):

y₁ 0, y₂ 0, …, y_m 0.

Построение двойственной задачи

Чтобы построить двойственную задачу необходимо привести экономико-математическую модель прямой задачи к стандартному виду. Матрица двойственной задачи строится путем транспонирования матрицы прямой задачи на 90 градусов, т.е. столбцы матрицы прямой задачи становятся строками двойственной задачи, а строки прямой задачи становится столбцами двойственной задачи, при этом:

1. Каждому ограничению прямой задачи соответствует переменная двойственной задачи.

2. Любой переменной прямой задачи соответствует ограничение двойственной задачи.

3. Коэффициенты при переменных целевой функции прямой задачи становятся свободными членами двойственной задачи.

4. Свободные члены прямой задачи становятся коэффициентами при переменных целевой функции двойственной задачи.

5. Если прямая задача решается на максимум, то двойственная задача – на минимум, и наоборот.

6. Если тип всех ограничений в прямой задаче «≥», то в двойственной задаче все ограничения изменяются на «≤», и наоборот.

В левой части системы ограничений двойственной задачи представлен общий расход ресурсов на единицу продукции, в правой части ограничений представлена единица продукции.

Целевая функция двойственной задачи – это общий (суммарный) расход ресурсов в оценках оптимального плана.

Двойственные оценки – это оценки продуктов, ресурсов, работ, выступающих в качестве ограничений в условиях решаемой оптимизационной задачи. Они показывают насколько изменится значение критерия оптимальности в прямой задаче при увеличении или уменьшении количества данного ресурса на единицу. Двойственные оценки являются искомыми переменными и оптимальным базисом (решением) двойственной задачи.

Открыты двойственные оценки академиком Л.В. Контаровичем. Он впервые охарактеризовал экономическое содержание двойственных оценок и их основные свойства. Двойственные оценки называют иначе – объективно обусловленными (оптимальными) оценками, множителями Лагранжа и целым рядом других терминов.

Двойственными оценками называют коэффициенты целевой строки последней симплексной таблицы, кроме значения целевой функции. На величину двойственной оценки изменяют значение целевой функции при изменении соответствующей небазисной переменной на единицу. Если решение не максимальное – значение целевой функции будет уменьшаться на величину двойственной оценки, если минимальное – увеличиваться.

Коэффициентами замещения (структурных сдвигов или коэффициентами пропорциональности) называют коэффициенты последней симплексной таблицы, расположенные на пересечении столбцов с небазисными переменными и строк базисными искомыми величинами.

Коэффициенты замещения указывают на возможность изменения решения при изменении начальных условий или введении дополнительных требований к решению задачи. Подобными изменениями обычно являются новые конкретные значения небазисных переменных оптимального решения.

Признак оптимальности двойственной задачи. Из теории двойственности следует, что максимум целевой функции прямой задачи равен минимуму целевой функции двойственной задачи. Это означает, что стоимость всей продукции прямой задачи равна общей оценке ресурсов, затраченных на производство в двойственной задаче. Отсутствие такого равенства говорит о неоптимальности решения.

Решают двойственные задачи так же, как и прямые. Решив двойственную задачу симплексным методом, получим оптимальное решение, в котором последняя симплексная таблица будет транспонированной. Поэтому коэффициенты целевой строки без свободного члена и получили название двойственных оценок. Решением в этой таблице будут коэффициенты целевой строки последней симплексной таблицы прямой задачи, т.е. двойственную задачу решать не обязательно, достаточно решить прямую.

Экономико-математический анализ оптимального решения рассмотрим на примере.

Задача 9. Хозяйственное подразделение располагает ресурсами: площадь пашни – 2200 га; трудовые ресурсы – 650750 тыс. час; механизированный труд – 2000 маш. смен. В хозяйстве планируется возделывать зерновые, сахарную свеклу, однолетние и многолетние травы на сено. Определить оптимальные размеры посевов указанных культур так, чтобы получить при заданной технологии возделывания максимальное количество валовой продукции и выполнить договорные обязательства по зерновым, которые составляют 16000 ц. Остальная данные представлены в таблице 28.

Таблица 28