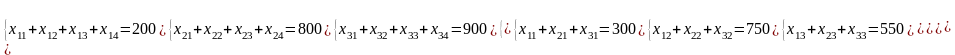- •Методы оптимальных решений
- •Содержание
- •Введение
- •1. Моделирование – метод научного познания
- •1.1 Основные понятия моделирования
- •Вопросы *
- •1.2 Системный подход и моделирование социально-экономических систем
- •Вопросы
- •5. Численное решение
- •6. Анализ численных результатов и их применение
- •Приемы экономико-математического моделирования
- •Классификация моделей по типу информации:
- •Классификация моделей по учету фактора времени:
- •Классификация моделей по учету фактора неопределенности:
- •Классификация моделей по типу подхода к изучаемым социально-экономическим системам:
- •Вопросы
- •2.2 Принцип оптимальности в планировании и управлении
- •Вопросы
- •Математическая формулировка общей задачи линейного программирования
- •Структурная форма записи задачи линейного программирования
- •Вопросы
- •3.2 Формы записи задачи линейного программирования
- •Нормы затрат и выхода продукции
- •Решение
- •Общая форма записи задачи линейного программирования
- •Каноническая форма записи задачи линейного программирования
- •Стандартная форма записи задачи линейного программирования
- •4.2. Алгоритм графического метода
- •Нормы затрат и выхода продукции
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Построение граничных прямых, соответствующих системе ограничений
- •3. Определение области допустимых решений
- •4. Построение вектора градиента и линии уровня
- •5. Нахождение точки экстремума
- •6. Определение значения целевой функции
- •4.3. Варианты графического решения задач линейного программирования
- •Вопросы
- •Рекомендуемые источники к главе 4
- •5. Симплексный метод решения задач линейного программирования
- •5.1. Сущность симплексного метода
- •Вопросы
- •5.2. Алгоритм решения задач симплексным методом с естественным базисом
- •Показатели эффективности возделывания 1 га культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса
- •4. Построение первой симплексной таблицы
- •Первая симплексная таблица (сокращенная)
- •Первая симплексная таблица (полная)
- •5. Проверка оптимальности решения
- •6. Построение второй симплексной таблицы
- •Первая симплексная таблица с разрешающим элементом
- •Вторая симплексная таблица
- •Правила нахождения коэффициентов второй симплексной таблицы
- •Вторая симплексная таблица
- •7. Построение третьей и последующих симплексных таблиц
- •Вторая симплексная таблица с разрешающим элементом
- •Третья симплексная таблица
- •Вопросы
- •5.3. Алгоритм решения задач симплексным методом с искусственным базисом
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса, введение искусственных переменных
- •4. Построение первой симплексной таблицы
- •Первая сокращенная симплексная таблица с м-строкой
- •5. Решение вспомогательной задачи симплексным методом с естественным базисом
- •Данные о содержании питательных веществ и стоимости культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса, введение искусственных переменных
- •4. Построение первой симплексной таблицы
- •Первая симплексная таблица
- •5. Проверка оптимальности решения
- •6. Построение второй симплексной таблицы
- •Первая симплексная таблица с разрешающим элементом
- •Вторая симплексная таблица
- •7. Построение третьей и последующих симплексных таблиц
- •Третья симплексная таблица
- •Вопросы
- •5.4. Алгоритм решения задач симплексным методом в Microsoft Excel 2010
- •Показатели эффективности возделывания 1 га культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Составление формы для ввода данных в Microsoft Excel
- •3. Ввод исходных данных в форму Microsoft Excel
- •4. Ввод формул для вычислений значений целевой функции и левой части неравенств
- •5. Настройка программы Microsoft Excel 2010
- •6. Установка значений в окне Параметры поиска решений
- •7. Анализ полученного решения
- •6.2. Постановка и математическая формулировка транспортной задачи
- •Постановка задачи
- •Матрица транспортной задачи
- •6.3. Алгоритм решения транспортной задачи (метод северо-западного угла)
- •Стоимости перевозок одной тонны картофеля (ден. Ед.)
- •Решение
- •1. Проверка типа задачи (открытая или закрытая)
- •2. Составление экономико-математической модели задачи
- •Матрица транспортной задачи (ден. Ед.)
- •3. Составление опорного плана
- •Опорный план транспортной задачи (ден. Ед.)
- •4. Проверка решения на оптимальность
- •Опорный план транспортной задачи (ден. Ед.)
- •5. Построение контура
- •Правила построения контура
- •Опорный план транспортной задачи с контуром (ден. Ед.)
- •6. Построение нового опорного плана
- •7. Проверка нового плана на оптимальность
- •Вопросы
- •6.4. Алгоритм решения транспортной задачи в Microsoft Excel 2010
- •Себестоимость перевозки 1 т сена, руб.
- •Решение
- •1. Проверка типа задачи (открытая или закрытая)
- •2. Составление экономико-математической модели задачи
- •6. Анализ полученного решения
- •Вопросы
- •6.5. Задача о назначениях
- •Общий вид транспортной матрицы задачи о назначениях
- •Экономико-математическая модель задачи о назначениях
- •Структурная форма записи задачи о назначениях
- •Вопросы и задания для самопроверки и самоподготовки
- •6.6. Алгоритм решения задачи о назначениях с помощью Microsoft Excel 2010
- •Производительность работников
- •Решение
- •1. Составление экономико-математической модели задачи
- •7.2 Прямая и двойственная задача
- •Построение двойственной задачи
- •Исходные данные задачи
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Решение задачи симплексным методом
- •Последняя симплексная таблица (оптимальное решение)
- •4. Анализ двойственных оценок
- •Симплексная таблица с коэффициентами замещения и двойственными оценками
- •Вопросы
- •7.3 Основные свойства двойственных оценок
- •Вопросы
- •7.4 Алгоритм решения двойственной задачи в Microsoft Excel 2010
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Решение задачи симплексным методом
- •3. Анализ оптимального решения
- •4. Мера влияния ограничения на целевую функцию
- •5. Свойство оптимальности решения
- •Вопросы
- •Рекомендуемые источники к главе 7
- •Библиографический список
- •Приложение 1 Полезные ссылки
Вопросы
Перечислите методы решения транспортных задач.
Объясните сущность распределительного метода решения задач линейного программирования.
Сформулируйте постановку транспортной задачи по критерию стоимости.
Напишите экономико-математическую модель транспортной задачи.
Раскройте особенности закрытых и открытых задач. Каким образом привести открытую задачу к закрытой?
В чем состоит проверка исходного плана транспортной задачи на вырожденность?
Каковы основные этапы алгоритма решения транспортной задачи?
Назовите элементы структуры экономико-математической модели транспортной задачи.
Перечислите способы построения начального (опорного) плана при решении транспортной задачи, раскройте их суть.
Что называется потенциалом строки (столбца) транспортной таблицы? Каким образом он вычисляется?
Как вычислить характеристику пустых клеток?
Дайте экономическую интерпретацию метода потенциалов решения транспортной задачи.
Сформулируйте правила построения замкнутого маршрута (контура) при решении транспортной задачи.
Каковы признаки оптимальности решения транспортной задачи, если задача решается на минимум, на максимум?
Каким образом строится новый опорный план?
Каким образом применяется распределительный метод решения транспортной задачи в исследованиях?
6.4. Алгоритм решения транспортной задачи в Microsoft Excel 2010
Рассмотрим алгоритм решения транспортной задачи.
Задача 7. В хозяйстве на стойловый период заготовлено 1900 т сена, которое сосредоточено на трех участках: на первом участке – 200 т, на втором – 800 т, на третьем – 900 т. Сено перевозится на четыре фермы, потребности которых следующие: на первую ферму необходимо завести 300 тонн сена, на вторую – 750 т, на третью – 550 т, на четвертую – 300 т. Себестоимость доставки одной тонны сена от участка до фермы различна (таблица 25). Необходимо составить план перевозки сена от участков до ферм минимизирующий общую стоимость перевозок и удовлетворяющий полностью потребности ферм в сене.
Таблица 25
Себестоимость перевозки 1 т сена, руб.
Номер участка |
Номер фермы |
|||
1 |
2 |
3 |
4 |
|
1 |
101 |
102 |
90 |
80 |
2 |
85 |
69 |
88 |
70 |
3 |
120 |
140 |
110 |
90 |
Решение
1. Проверка типа задачи (открытая или закрытая)
Определим количество сена на участках и количество сена, необходимого фермам, и сравним полученные суммы. Количество сена на участках составляет: 200 + 800 + 900 = 1900 (т). Количество сена, необходимого фермам, составляет: 300 + 750 + 550 + 300 = 1900 (т). В данном случае суммы равны, поэтому задача закрытого типа, т.е. все сено можно перевезти с участков и поставить в необходимом количестве на фермы.
2. Составление экономико-математической модели задачи
Введем обозначения: xij – количество сена, перевозимого с i-го участка на j-ю ферму (где i = 1, 2,…, 3 и j = 1,…, 4).
Найти минимальное значение: Zmin = 101х11 + 102х12 + 90х13 + 80х14 + 85х21 + 69х22 + 88х23 + 70х24 +120х31 + 140х32 + 110х33 + 90х34, при условиях неотрицательности переменных xij (xij ≥ 0) и ограничениях:
|
Ограничения по участкам – ограничение на количество сена на первом участке, т – ограничение на количество сена на втором участке, т – ограничение на количество сена на третьем участке, т Ограничения по фермам – ограничение на количество сена для первой фермы, т – ограничение на количество сена для второй фермы, т – ограничение на количество сена для третьей фермы, т – ограничение на количество сена для четвертой фермы, т |
3. Составление формы для ввода данных в Microsoft Excel
Создайте Книгу в Microsoft Excel и сохраните ее. Оформите таблицы как показано на рисунке 25 и введите исходные данные.

Рис. 25 – Исходные данные задачи и формы для вычислений
3. Ввод формул
Введите в матрице назначений формулы для вычисления количества сена, необходимого фермам (суммы по столбцам в ячейках), количества сена на участках (суммы по строкам) и значения целевой функции (сумма произведений коэффициентов целевой функции и значений переменных) как показано на рисунке 26.

Рис. 26 – Формулы для вычислений значений целевой функции и количества сена
4. Настройка программы Microsoft Excel 2010
Команда Поиск решения находится во вкладке Данные (с. 63).
5. Установка значений в окне Параметры поиска решений
Откройте окно Поиска решений и введите (рис. 27, 28):
адрес ячейки со значением целевой функции – F19 (щелчком левой кнопки мыши);
установите режим Минимум;
в поле Изменяя ячейки переменных укажите диапазон C14:F16, в которых программа подберет оптимальные значения переменных x1 и х2;
добавьте ограничения с помощью кнопки Добавить (рис. 28). Для этого используется щелчок левой кнопки мыши по необходимым ячейкам, а знак неравенства или равенства выбирается из списка в окне Добавление ограничения (рис. 29);
укажите метод решения Поиск решения линейных задач симплексным методом (рис. 28);
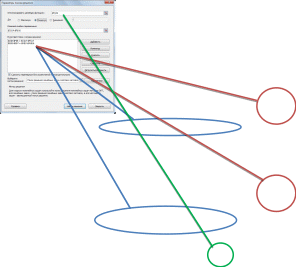


Рис. 27 – Установки окна Параметры поиска решений

Рис. 28 – Окно Параметры поиска решений

Рис. 29 – Окно Изменение ограничений
нажмите кнопку Найти решение (рис. 28);
в окне Результаты поиска решения выберите режим Сохранить найденное решение и нажмите ОК (рис. 23).