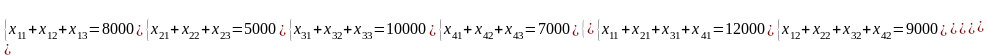- •Методы оптимальных решений
- •Содержание
- •Введение
- •1. Моделирование – метод научного познания
- •1.1 Основные понятия моделирования
- •Вопросы *
- •1.2 Системный подход и моделирование социально-экономических систем
- •Вопросы
- •5. Численное решение
- •6. Анализ численных результатов и их применение
- •Приемы экономико-математического моделирования
- •Классификация моделей по типу информации:
- •Классификация моделей по учету фактора времени:
- •Классификация моделей по учету фактора неопределенности:
- •Классификация моделей по типу подхода к изучаемым социально-экономическим системам:
- •Вопросы
- •2.2 Принцип оптимальности в планировании и управлении
- •Вопросы
- •Математическая формулировка общей задачи линейного программирования
- •Структурная форма записи задачи линейного программирования
- •Вопросы
- •3.2 Формы записи задачи линейного программирования
- •Нормы затрат и выхода продукции
- •Решение
- •Общая форма записи задачи линейного программирования
- •Каноническая форма записи задачи линейного программирования
- •Стандартная форма записи задачи линейного программирования
- •4.2. Алгоритм графического метода
- •Нормы затрат и выхода продукции
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Построение граничных прямых, соответствующих системе ограничений
- •3. Определение области допустимых решений
- •4. Построение вектора градиента и линии уровня
- •5. Нахождение точки экстремума
- •6. Определение значения целевой функции
- •4.3. Варианты графического решения задач линейного программирования
- •Вопросы
- •Рекомендуемые источники к главе 4
- •5. Симплексный метод решения задач линейного программирования
- •5.1. Сущность симплексного метода
- •Вопросы
- •5.2. Алгоритм решения задач симплексным методом с естественным базисом
- •Показатели эффективности возделывания 1 га культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса
- •4. Построение первой симплексной таблицы
- •Первая симплексная таблица (сокращенная)
- •Первая симплексная таблица (полная)
- •5. Проверка оптимальности решения
- •6. Построение второй симплексной таблицы
- •Первая симплексная таблица с разрешающим элементом
- •Вторая симплексная таблица
- •Правила нахождения коэффициентов второй симплексной таблицы
- •Вторая симплексная таблица
- •7. Построение третьей и последующих симплексных таблиц
- •Вторая симплексная таблица с разрешающим элементом
- •Третья симплексная таблица
- •Вопросы
- •5.3. Алгоритм решения задач симплексным методом с искусственным базисом
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса, введение искусственных переменных
- •4. Построение первой симплексной таблицы
- •Первая сокращенная симплексная таблица с м-строкой
- •5. Решение вспомогательной задачи симплексным методом с естественным базисом
- •Данные о содержании питательных веществ и стоимости культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса, введение искусственных переменных
- •4. Построение первой симплексной таблицы
- •Первая симплексная таблица
- •5. Проверка оптимальности решения
- •6. Построение второй симплексной таблицы
- •Первая симплексная таблица с разрешающим элементом
- •Вторая симплексная таблица
- •7. Построение третьей и последующих симплексных таблиц
- •Третья симплексная таблица
- •Вопросы
- •5.4. Алгоритм решения задач симплексным методом в Microsoft Excel 2010
- •Показатели эффективности возделывания 1 га культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Составление формы для ввода данных в Microsoft Excel
- •3. Ввод исходных данных в форму Microsoft Excel
- •4. Ввод формул для вычислений значений целевой функции и левой части неравенств
- •5. Настройка программы Microsoft Excel 2010
- •6. Установка значений в окне Параметры поиска решений
- •7. Анализ полученного решения
- •6.2. Постановка и математическая формулировка транспортной задачи
- •Постановка задачи
- •Матрица транспортной задачи
- •6.3. Алгоритм решения транспортной задачи (метод северо-западного угла)
- •Стоимости перевозок одной тонны картофеля (ден. Ед.)
- •Решение
- •1. Проверка типа задачи (открытая или закрытая)
- •2. Составление экономико-математической модели задачи
- •Матрица транспортной задачи (ден. Ед.)
- •3. Составление опорного плана
- •Опорный план транспортной задачи (ден. Ед.)
- •4. Проверка решения на оптимальность
- •Опорный план транспортной задачи (ден. Ед.)
- •5. Построение контура
- •Правила построения контура
- •Опорный план транспортной задачи с контуром (ден. Ед.)
- •6. Построение нового опорного плана
- •7. Проверка нового плана на оптимальность
- •Вопросы
- •6.4. Алгоритм решения транспортной задачи в Microsoft Excel 2010
- •Себестоимость перевозки 1 т сена, руб.
- •Решение
- •1. Проверка типа задачи (открытая или закрытая)
- •2. Составление экономико-математической модели задачи
- •6. Анализ полученного решения
- •Вопросы
- •6.5. Задача о назначениях
- •Общий вид транспортной матрицы задачи о назначениях
- •Экономико-математическая модель задачи о назначениях
- •Структурная форма записи задачи о назначениях
- •Вопросы и задания для самопроверки и самоподготовки
- •6.6. Алгоритм решения задачи о назначениях с помощью Microsoft Excel 2010
- •Производительность работников
- •Решение
- •1. Составление экономико-математической модели задачи
- •7.2 Прямая и двойственная задача
- •Построение двойственной задачи
- •Исходные данные задачи
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Решение задачи симплексным методом
- •Последняя симплексная таблица (оптимальное решение)
- •4. Анализ двойственных оценок
- •Симплексная таблица с коэффициентами замещения и двойственными оценками
- •Вопросы
- •7.3 Основные свойства двойственных оценок
- •Вопросы
- •7.4 Алгоритм решения двойственной задачи в Microsoft Excel 2010
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Решение задачи симплексным методом
- •3. Анализ оптимального решения
- •4. Мера влияния ограничения на целевую функцию
- •5. Свойство оптимальности решения
- •Вопросы
- •Рекомендуемые источники к главе 7
- •Библиографический список
- •Приложение 1 Полезные ссылки
6.3. Алгоритм решения транспортной задачи (метод северо-западного угла)
Рассмотрим алгоритм решения транспортной задачи на конкретном примере.
Задача 6. Из четырех складов, необходимо перевести картофель в три магазина, расположенных в различных пунктах. В первом складе хранится 8000 т картофеля, во втором – 5000 т, в третьем – 10000 т, в четвертом – 7000 т. Потребность первого магазина в картофеле составляет 12000 т, второго – 9000 т, третьего – 9000 т. Стоимости перевозок одной тонны картофеля со складов в магазины представлены в таблице 19.
Таблица 19
Стоимости перевозок одной тонны картофеля (ден. Ед.)
Номер склада |
Номер магазина |
||
1 |
2 |
3 |
|
1 |
40 |
70 |
20 |
2 |
10 |
20 |
30 |
3 |
30 |
40 |
10 |
4 |
30 |
20 |
50 |
Требуется составить план перевозок, минизирующий затраты на транспортировку картофеля, при этом весь груз необходимо вывести, а потребности магазинов удовлетворить.
Решение
1. Проверка типа задачи (открытая или закрытая)
Находим количество запасов картофеля на складах и количество картофеля, необходимого магазинам, и сравниваем полученные суммы:
Количество картофеля, хранимого на складах, составляет 30000 тонн, т.к.
8000 + 5000 + 10000 + 7000 = 30000 (т).
Количество картофеля, необходимого магазинам:
12000 + 9000 + 9000 = 30000 (т).
В данном случае суммы равны, поэтому данная задача закрытого типа, т.е. весь картофель можно вывести со складов и поставить в необходимом количестве во все магазины.
2. Составление экономико-математической модели задачи
Обозначим: xij – количество картофеля, перевозимого из i-го склада (i = 1, 2,…, 4) в j-ый магазин (j = 1, 2, …, 3).
Экономико-математическая модель задачи в общей форме:
Найти значения переменных xij, которое бы обеспечивало минимальное значение целевой функции Zmin = 40х11 + 70х12 + 20х13 + 10х21 + 20х22 + 30х23 +30х31 + 40х32 + 10х33 + 30х41 + 20х42 + 50х43, при условиях неотрицательности переменных xij (xij ≥ 0) и ограничениях:
|
Ограничения по поставщикам – ограничение по количеству картофеля в первом складе, т – ограничение по количеству картофеля во втором складе, т – ограничение по количеству картофеля в третьем складе, т – ограничение по количеству картофеля в четвертом складе, т Ограничения по потребителям – ограничение по количеству картофеля в первом магазине, т – ограничение по количеству картофеля во втором магазине, т – ограничение по количеству картофеля в третьем магазине, т |
Данные задачи наглядно можно представить в таблице 20.
Таблица 20
Матрица транспортной задачи (ден. Ед.)
Номер склада (Ai) |
Номер магазина (Bj) |
Количество груза на складах (ai) |
|||||
1 |
2 |
3 |
|||||
1 |
40 |
|
70 |
|
20 |
|
8000 |
|
x11 |
|
x12 |
|
x13 |
||
Стоимость
перевозки
со
склада
в
магазин (сij) |
10 |
|
20 |
|
30 |
|
5000 |
|
x21 |
|
x22 |
|
x23 |
||
3 |
30 |
|
40 |
|
10 |
|
10000 |
|
x31 |
|
x32 |
|
x33 |
||
4 |
30 |
|
20 |
|
50 |
|
7000 |
|
x41 |
|
x42 |
|
x43 |
||
Количество груза в магазинах (bj) |
12000 |
9000 |
9000 |
Количество
перевозимого груза
со склада
(xij)
в
магазин |
|||