Решение

1. Составление экономико-математической модели задачи

Экономико-математическая модель задачи в общей форме: Найти значение неизвестных, которое бы обеспечивало максимальное значение целевой функции Z_max при соблюдении ограничений и условий неотрицательности переменных:

1) целевая функция: Z_max = с₁х₁ + с₂х₂ (Z_min = с₁х₁ + с₂х₂);

2) система ограничений:

;

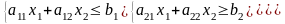3) условия неотрицательности: x₁≥ 0, x₂ ≥ 0.

2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных

Экономико-математическая модель задачи в канонической форме: Найти значение неизвестных, которое бы обеспечивало экстремальное значение целевой функции при соблюдении ограничений и условий неотрицательности переменных:

1) целевая функция: Z_max = с₁х₁ + с ₂х₂ + 0S₁ + 0S₂ + 0S₃

(Z_min = с ₁х₁ + с ₂х₂ + 0S₁ + 0S₂ + 0S₃);

2) система ограничений в канонической форме:

;

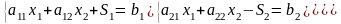3) условия неотрицательности: x₁≥ 0, x₂ ≥ 0, S₁ ≥ 0, S₂ ≥ 0, S₃ ≥ 0.

Переменные х₁, х₂ – основные, S₁, S₂, S₃ – дополнительные.

3. Составление базиса, введение искусственных переменных

Выразим в системе ограничений дополнительные переменные:

.

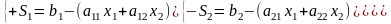Переменные S2, S3 со знаком «-», поэтому они не могут быть базисными. Необходимо ввести искусственные базисные переменные y₂, y₃ и M-строку.

.

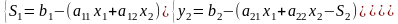
В данной записи переменные S₁, у₂, у₃ являются базисными, а остальные – свободными переменными (х₁, х₂ и S₂, S₃).

Целевую функцию изменим по правилам решения задач симплексным методом с искусственными переменными:

Z_max = 0 – (-с₁х₁ – с₂х₂), M_max = (b₂ + b₃) – (m₁х₁ + m₂х₂ – S₂ – S₃)

(Z_min = 0 – (-с₁х₁ – с₂х₂), M_min = (b₂ + b₃) + (m₁х₁ + m₂х₂ – S₂ – S₃)),

где m₁ = a₂₁+a₃₁, m₂ = a₂₂+a₃₂.

4. Построение первой симплексной таблицы

Строим и заполняем первую симплексную таблицу (таблица 11):

• указываем коэффициенты при свободных переменных и свободные члены из системы ограничений и целевой функции как в решении задач симплексным методом с естественным базисом;

• дополняем таблицу M-строкой, элементы которой равны сумме коэффициентов перед свободными переменными и свободными членами тех ограничений, в которых введена искусственная базисная переменная (М-строка равна сумме строк с искусственными переменными).

Таблица 11

Первая сокращенная симплексная таблица с м-строкой

Базис	Свободные члены, bi	Свободные переменные
		- х1	- х2	- S2	- S3
S1	b1	a11	a12	0	0
у2	b2	a21	a22	-1	0
у3	b3	a31	a32	0	-1
Zmax	0	с1	с2	0	0
M	b2 + b3	m1 = a21+a31	m2 = a22+a32	-1	-1

5. Решение вспомогательной задачи симплексным методом с естественным базисом

Выполняются этапы 5-7 симплексного метода решения задач с естественным базисом.

Для улучшения решения, аналогично решению задач с естественным базисом, находим разрешающий столбец, разрешающую строку, разрешающий элемент и по тем же шагам заполняем любую симплексную таблицу.

Разрешающий столбец при решении задач симплексным методом на максимум и минимум с искусственным базисом находится по наибольшему положительному коэффициенту М-строки до тех пор, пока она существует (пока М-строка не стала равна 0). Как только М-строка равна 0, а решение не оптимальное, разрешающий столбец будет определяться по Z строке: при решении задач на максимум – по наименьшему отрицательному коэффициенту Z-строки, на минимум – по наибольшему положительному коэффициенту Z-строки.

Если базисная искусственная переменная становится свободной, то соответствующий ей столбец удаляют из таблицы. Исключенные из базиса искусственные переменные повторно вводить не имеет смысла, поэтому коэффициенты в столбцах этих переменных не вычисляют и при последующих итерациях исключают.

Дополнительные переменные никогда не исключаются, т.к. каждая дополнительная переменная имеет определенный экономический смысл. Основные и дополнительные переменные могут несколько раз перемещаться в базис и обратно.

Другие коэффициенты таблицы вычисляют по правилу прямоугольника.

Рассмотрим алгоритм решения задачи симплексным методом с искусственным базисом на примере.

Задача 5. Составить рацион с минимальной себестоимостью для кормления коровы, при условии, что животному необходимо дать не менее 13 кг кормовых единиц и 1500 г перевариваемого протеина. Общий вес рациона не должен превышать 50 кг. Рацион состоит из ячменя и люцерны. Данные о содержании питательных веществ и стоимости культур приведены в таблице 12.

Таблица 12