
- •Методы оптимальных решений
- •Содержание
- •Введение
- •1. Моделирование – метод научного познания
- •1.1 Основные понятия моделирования
- •Вопросы *
- •1.2 Системный подход и моделирование социально-экономических систем
- •Вопросы
- •5. Численное решение
- •6. Анализ численных результатов и их применение
- •Приемы экономико-математического моделирования
- •Классификация моделей по типу информации:
- •Классификация моделей по учету фактора времени:
- •Классификация моделей по учету фактора неопределенности:
- •Классификация моделей по типу подхода к изучаемым социально-экономическим системам:
- •Вопросы
- •2.2 Принцип оптимальности в планировании и управлении
- •Вопросы
- •Математическая формулировка общей задачи линейного программирования
- •Структурная форма записи задачи линейного программирования
- •Вопросы
- •3.2 Формы записи задачи линейного программирования
- •Нормы затрат и выхода продукции
- •Решение
- •Общая форма записи задачи линейного программирования
- •Каноническая форма записи задачи линейного программирования
- •Стандартная форма записи задачи линейного программирования
- •4.2. Алгоритм графического метода
- •Нормы затрат и выхода продукции
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Построение граничных прямых, соответствующих системе ограничений
- •3. Определение области допустимых решений
- •4. Построение вектора градиента и линии уровня
- •5. Нахождение точки экстремума
- •6. Определение значения целевой функции
- •4.3. Варианты графического решения задач линейного программирования
- •Вопросы
- •Рекомендуемые источники к главе 4
- •5. Симплексный метод решения задач линейного программирования
- •5.1. Сущность симплексного метода
- •Вопросы
- •5.2. Алгоритм решения задач симплексным методом с естественным базисом
- •Показатели эффективности возделывания 1 га культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса
- •4. Построение первой симплексной таблицы
- •Первая симплексная таблица (сокращенная)
- •Первая симплексная таблица (полная)
- •5. Проверка оптимальности решения
- •6. Построение второй симплексной таблицы
- •Первая симплексная таблица с разрешающим элементом
- •Вторая симплексная таблица
- •Правила нахождения коэффициентов второй симплексной таблицы
- •Вторая симплексная таблица
- •7. Построение третьей и последующих симплексных таблиц
- •Вторая симплексная таблица с разрешающим элементом
- •Третья симплексная таблица
- •Вопросы
- •5.3. Алгоритм решения задач симплексным методом с искусственным базисом
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса, введение искусственных переменных
- •4. Построение первой симплексной таблицы
- •Первая сокращенная симплексная таблица с м-строкой
- •5. Решение вспомогательной задачи симплексным методом с естественным базисом
- •Данные о содержании питательных веществ и стоимости культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса, введение искусственных переменных
- •4. Построение первой симплексной таблицы
- •Первая симплексная таблица
- •5. Проверка оптимальности решения
- •6. Построение второй симплексной таблицы
- •Первая симплексная таблица с разрешающим элементом
- •Вторая симплексная таблица
- •7. Построение третьей и последующих симплексных таблиц
- •Третья симплексная таблица
- •Вопросы
- •5.4. Алгоритм решения задач симплексным методом в Microsoft Excel 2010
- •Показатели эффективности возделывания 1 га культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Составление формы для ввода данных в Microsoft Excel
- •3. Ввод исходных данных в форму Microsoft Excel
- •4. Ввод формул для вычислений значений целевой функции и левой части неравенств
- •5. Настройка программы Microsoft Excel 2010
- •6. Установка значений в окне Параметры поиска решений
- •7. Анализ полученного решения
- •6.2. Постановка и математическая формулировка транспортной задачи
- •Постановка задачи
- •Матрица транспортной задачи
- •6.3. Алгоритм решения транспортной задачи (метод северо-западного угла)
- •Стоимости перевозок одной тонны картофеля (ден. Ед.)
- •Решение
- •1. Проверка типа задачи (открытая или закрытая)
- •2. Составление экономико-математической модели задачи
- •Матрица транспортной задачи (ден. Ед.)
- •3. Составление опорного плана
- •Опорный план транспортной задачи (ден. Ед.)
- •4. Проверка решения на оптимальность
- •Опорный план транспортной задачи (ден. Ед.)
- •5. Построение контура
- •Правила построения контура
- •Опорный план транспортной задачи с контуром (ден. Ед.)
- •6. Построение нового опорного плана
- •7. Проверка нового плана на оптимальность
- •Вопросы
- •6.4. Алгоритм решения транспортной задачи в Microsoft Excel 2010
- •Себестоимость перевозки 1 т сена, руб.
- •Решение
- •1. Проверка типа задачи (открытая или закрытая)
- •2. Составление экономико-математической модели задачи
- •6. Анализ полученного решения
- •Вопросы
- •6.5. Задача о назначениях
- •Общий вид транспортной матрицы задачи о назначениях
- •Экономико-математическая модель задачи о назначениях
- •Структурная форма записи задачи о назначениях
- •Вопросы и задания для самопроверки и самоподготовки
- •6.6. Алгоритм решения задачи о назначениях с помощью Microsoft Excel 2010
- •Производительность работников
- •Решение
- •1. Составление экономико-математической модели задачи
- •7.2 Прямая и двойственная задача
- •Построение двойственной задачи
- •Исходные данные задачи
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Решение задачи симплексным методом
- •Последняя симплексная таблица (оптимальное решение)
- •4. Анализ двойственных оценок
- •Симплексная таблица с коэффициентами замещения и двойственными оценками
- •Вопросы
- •7.3 Основные свойства двойственных оценок
- •Вопросы
- •7.4 Алгоритм решения двойственной задачи в Microsoft Excel 2010
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Решение задачи симплексным методом
- •3. Анализ оптимального решения
- •4. Мера влияния ограничения на целевую функцию
- •5. Свойство оптимальности решения
- •Вопросы
- •Рекомендуемые источники к главе 7
- •Библиографический список
- •Приложение 1 Полезные ссылки
Стандартная форма записи задачи линейного программирования
Приведем систему ограничений к стандартной форме. Для этого знак последнего неравенства «≥» (отличный от знаков остальных неравенств) необходимо заменить на знак «≤». Поэтому левую и правую часть последнего неравенства (15х1 ≥ 5000) умножим на -1 и изменим знак неравенства.
Экономико-математическая модель задачи в стандартной форме:
Найти значения неизвестных, которое бы обеспечивало максимальное значение целевой функции Zmax при соблюдении ограничений и условий неотрицательности переменных:
1) целевая функция: Zmax = 400х1 + 100х2;
2) система ограничений в стандартной форме:
;
3) условия неотрицательности: х1 ≥ 0, х2 ≥ 0.
Вопросы
Какие формы записи задач линейного программирования существуют?
В чем отличие форм записи задачи линейного программирования?
Что такое эквивалентность форм записи задачи линейного программирования?
Приведите примеры форм записи задач линейного программирования.
Рекомендуемые источники к главе 3
4, 7, 15, 22
4. Геометрическое представление задачи линейного программирования. Графический метод
4.1. Геометрическая интерпретация задачи линейного программирования
Методы решения экономико-математических задач можно разделить на две группы:
универсальные, которые наиболее распространены, среди них широко известен симплексный метод;
специальные, к ним относятся распределительный метод, транспортная задача, графический метод.
Графический метод основан на геометрической интерпретации задач линейного программирования в простейших случаях. Этот способ применяется при решении задач небольшой размерности, когда число переменных не превышает трех (рис. 1).

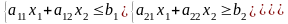
Рис. 1 – Пересечение полуплоскостей |
Этот метод позволяет решать задачи двумерного пространства и только некоторые задачи трехмерного пространства, т.к. трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически достаточно сложно.
Геометрическую интерпретацию задачи линейного программирования рассмотрим на примере задачи с двумя переменными. Каждое из неравенств задачи линейного программирования определяет на координатной плоскости некоторую полуплоскость (рис. 2), а система неравенств в целом – пересечение соответствующих полуплоскостей (рис. 1).

Рис. 2 – Граничная прямая l1
и полуплоскость – решение неравенства a11x1 + a12x2 ≥ b1
Каждое неравенство в системе ограничений
делит плоскость на полуплоскости, на
одной из которых все точки ему
удовлетворяют, а на другой не удовлетворяют.
Прямая, расположенная между этими
полуплоскостями, называется граничной
прямой (рис. 2). Чтобы построить граничную
прямую, необходимо определить координаты
двух точек этой прямой. Для простоты
вычисления координат точек находят
координаты пересечения прямой с осями
координат. Например, на рисунке 2, чтобы
построить граничную прямую l1,
определены координаты точек пересечения
с осями координат A
(0;
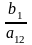 )
и B (
)
и B (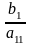 ;
0).
;
0).
Множество точек пересечения решений неравенств является областью допустимых решений (ОДР) (рис. 1).
Каждая из точек области допустимых решений является допустимым вариантом плана. Например, произвольно взятая точка F удовлетворяет всем условиям задачи. Если подставить координаты этой точки в систему ограничений, то можно увидеть, что вариант плана, соответствующий точке F, является допустимым, но не оптимальным, поскольку все ресурсы будут недоиспользованы.
Область допустимых решений представляет собой выпуклое множество, т.е. обладает свойством: если две точки P и G принадлежат этому множеству, то и весь отрезок, соединяющий точки P и G принадлежит ему (рис. 3).
 Область
допустимых решений графически может
быть представлена выпуклым многоугольником,
неограниченной выпуклой многоугольной
областью, отрезком, лучом, одной точкой
(рис. 4-7). В случае несовместности системы
ограничений задачи область допустимых
решений является пустым множеством
(рис. 8) [15].
Область
допустимых решений графически может
быть представлена выпуклым многоугольником,
неограниченной выпуклой многоугольной
областью, отрезком, лучом, одной точкой
(рис. 4-7). В случае несовместности системы
ограничений задачи область допустимых
решений является пустым множеством
(рис. 8) [15].
Рис. 3 ABCDK – выпуклый многоугольник.
|
Рис. 4 Область допустимых решений закрытая.
|
Рис. 5 Область допустимых решений открытая. Оптимальное решение достигается в точке B'. |
Рис. 6 Область допустимых решений открытая. Оптимальное решение достигается на отрезке B'C'. |


Рис. 7 Область допустимых решений вырождается в точку. Оптимальное решение достигается в точке А" |
Рис. 8 Область допустимых решений – пустое множество. Оптимальное решение отсутствует |
В теории линейного программирования доказано, что экстремальное значение целевой функции (если оно существует) обязательно достигается на границе выпуклого многоугольника или выпуклой многоугольной области с конечным числом угловых точек. Такой многоугольник называется симплексом. Метод заключается в направленном переборе вершин симплекса до получения оптимального плана. Следовательно, оптимальный вариант плана можно найти, последовательно перебирая варианты сочетаний х1 и х2 в вершинах многоугольника, однако это достаточно трудоемко.
Чтобы найти экстремальное значение в области допустимых решений необходимо построить вектор-градиент и линию уровня, а затем переместить линию уровня вдоль градиента до крайней точки многоугольника решений. Таким образом будут определены прямые, пересечение которых соответствует экстремальному значению целевой функции. Координаты точки пересечения этих прямых являются искомыми величинами, т.е. решением задачи. Вычисление координат точки экстремума происходит посредством решения системы уравнений для тех прямых, которые пересекаются в этой точке.
Градиентом функции
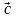 =
gradZ=
=
gradZ= называется вектор частных производных
этой функции. Градиент указывает
направление наиболее быстрого возрастания
функции и направлен перпендикулярно
линиям уровня (рис. 9).
называется вектор частных производных
этой функции. Градиент указывает
направление наиболее быстрого возрастания
функции и направлен перпендикулярно
линиям уровня (рис. 9).
Для функции Z(x) = c1x1 + c2x2 начало вектора-градиента находится в точке с координатами (0;0), конец – в точке (c1; c2) (рис. 9).


Рис. 9
Градиент
линия уровня Z(x) = 0 |
Рис. 10 Линии уровня функции Z(x) |
Целевая функция Z(x) = c1x1 + c2x2 при фиксированном значении Z(x) равном L определяет на плоскости прямую линию. Изменяя значения L, получим семейство параллельных прямых, называемых линиями уровня (рис. 10).
Прямые (линии уровня) параллельны, так как изменение значения L влечет изменение длин отрезков, отсекаемых линией уровня на осях, а угловой коэффициент α прямой останется постоянным. Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L. Линии уровня характеризуются тем, что во всех точках одной линии уровня значения функции Z(x) равны между собой.
Линию уровня функции Z(х) можно построить по двум точкам, приравняв целевую функцию к любому числу или проведя перпендикуляр к вектору-градиенту в любой его точке. В данном случае первую линию уровня проведем через точку О (0;0), перпендикулярно вектору-градиенту (рис. 9, 11).
Геометрически отыскание оптимального решения – это нахождение такой точки области допустимых решений, через которую проходит линия уровня целевой функции Zmax (Zmin), соответствующая наибольшему (наименьшему) значению функции Z(x). Оптимальное решение (если оно существует) находится в крайней точке многоугольника области допустимых решений, через которую пройдет целевая прямая, или на всей его стороне (рис. 4-7, 11).

Рис. 11 – Оптимальное решение в точке А
|
При решении задач на максимум для определения точки экстремума линия уровня перемещается по направлению вектора-градиента до тех пор, пока она не достигнет последней точки выхода из области допустимых решений.
При решении задач на минимум линию уровня перемещают в направлении противоположном вектору-градиенту до тех пор, пока она не достигнет последней точки выхода из области допустимых решений.


 Оптимальное
решение достигается на отрезке BC
Оптимальное
решение достигается на отрезке BC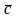 функции Z(x),
функции Z(x),