
- •Розв’язати систему рівнянь методом Гаусса:
- •Знайти ранг матриці .
- •Розв’язати матричне рівняння, зробити перевірку.
- •Розв’язати систему лінійних рівнянь a) за формулами Крамера;
- •Знайти ранг матриці .
- •Розв’язати систему лінійних рівнянь a) за формулами Крамера;
- •Розв’язати систему рівнянь методом Гаусса:
- •Знайти ранг матриці .
- •Розв’язати матричне рівняння, зробити перевірку
- •Розв’язати систему лінійних рівнянь a) за формулами Крамера;
- •Знайти ранг матриці .
- •Знайти ранг матриці .
- •Обчислити визначник
- •Знайти ранг матриці .
- •Обчислити визначник
- •Знайти значення матричного многочлена , якщо е – одинична матриця 3-го порядку,
- •Знайти ранг матриці .
- •Обчислити визначник
- •Розв’язати систему лінійних рівнянь a) за формулами Крамера;
- •Розв’язати систему рівнянь методом Гаусса:
- •Знайти ранг матриці .
- •Розв’язати систему лінійних рівнянь a) за формулами Крамера;
- •Розв’язати систему рівнянь методом Гаусса:
- •Знайти ранг матриці .
- •Розв’язати матричне рівняння, зробити перевірку.
- •Розв’язати систему лінійних рівнянь a) за формулами Крамера;
- •Знайти ранг матриці .
- •Розв’язати систему лінійних рівнянь а) за формулами Крамера;
- •Знайти ранг матриці .
- •Обчислити визначник
- •Знайти ранг матриці .
- •Розв’язати систему рівнянь методом Гаусса:
- •Знайти ранг матриці .
- •Розв’язати систему лінійних рівнянь a) за формулами Крамера;
- •Розв’язати систему рівнянь методом Гаусса:
- •Знайти ранг матриці .
- •Розв’язати систему лінійних рівнянь а) за формулами Крамера;
- •Розв’язати систему рівнянь методом Гаусса:
- •Знайти ранг матриці .
Розв’язати матричне рівняння, зробити перевірку.
![]() .
.
Розв’язати систему лінійних рівнянь a) за формулами Крамера;
б) матричним методом.
![]()
Визначити, при яких значеннях а система рівнянь a) має єдиний розв’язок (визначена); б) не має розв’язків (несумісна).
![]()
Знайти ранг матриці .
Варіант 17
Користуючись властивостями визначників, спочатку спростити, а потім обчислити визначник
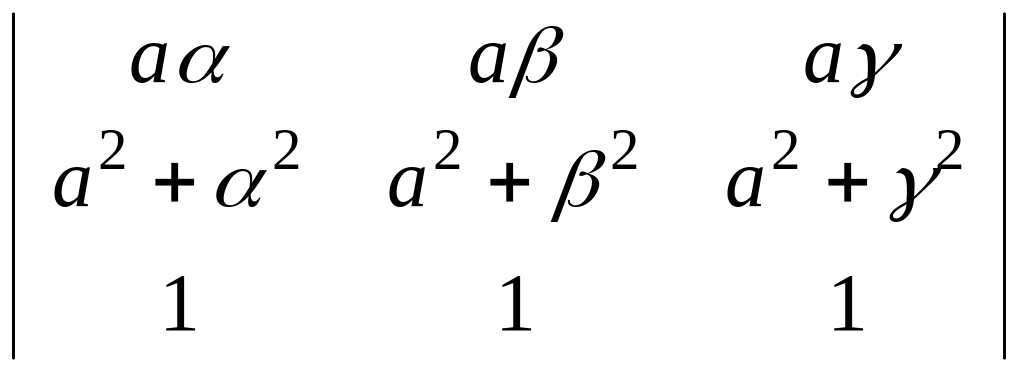 .
.
Вказівка.
Винести
а
за знак визначника;
Iст.-
IIIст.
; IIст.-IIIст.
;винести
![]() та
та
![]() за знак визначника.
за знак визначника.
Перетворивши в нуль всі,крім одного, елементи стовпця чи рядка, обчислити визначник
 .
.
Довести, що матриця X=
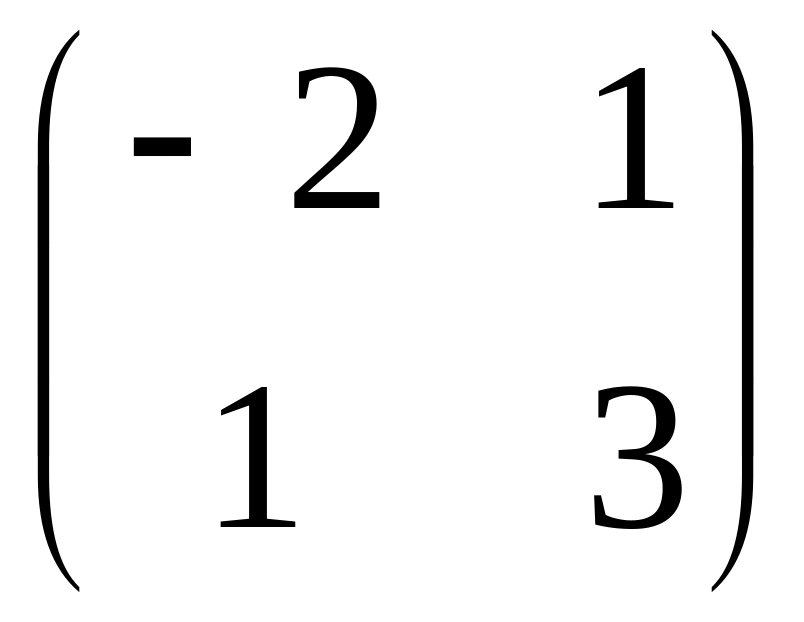 є
розв’язком рівняння
X2-X-7E=О,
де
E–одинична
матриця 2-го порядку.
є
розв’язком рівняння
X2-X-7E=О,
де
E–одинична
матриця 2-го порядку.
Знайти матрицю F=AB-BA, якщо
A= ;
B=
;
B= .
.
Яку матрицю C потрібно відняти від матриці FТ, щоб дістати одиничну матрицю?
Розв’язати матричне рівняння AXB=C, якщо
A=![]() ,
B=
,
B=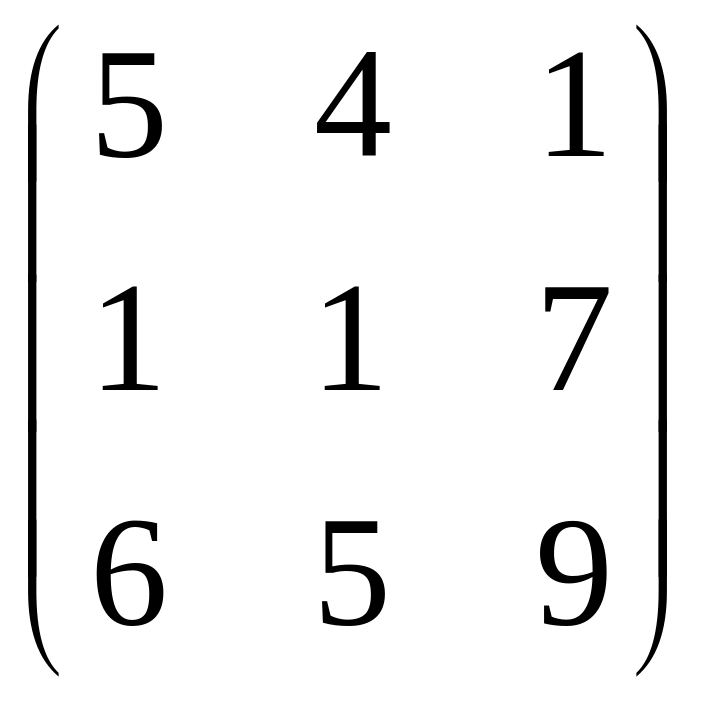 ,
C=
,
C=![]() .
.
Зробити перевірку.
Розв’язати систему лінійних рівнянь а) за формулами Крамера;
б) матричним методом.
![]()
Дослідити на сумісність систему використовуючи метод Гаусса:
![]() .
.
Знайти ранг матриці .
Варіант 18
Користуючись властивостями визначників, довести тотожність (визначник не розкривати):

Вказівка. Подати визначник у вигляді суми двох визначників. Перший із них дорівнює 0, другий привести до трикутного вигляду. Такий визначник дорівнює добутку його діагональних елементів.
Обчислити визначник
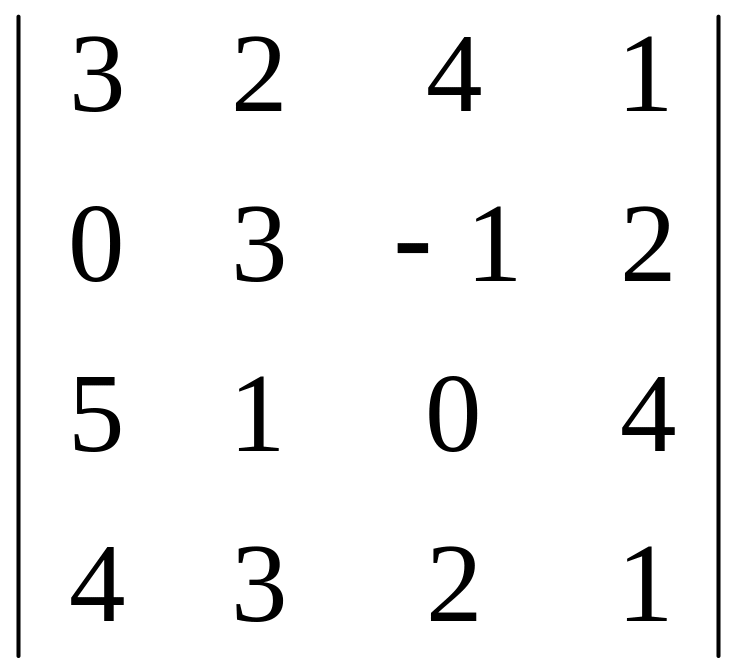 .
.
Знайти значення матричного многочлена
![]() ,
,
якщо Е
– одинична матриця 2-го порядку,
![]() .
.
Знайти добуток матриць АВС, якщо
;
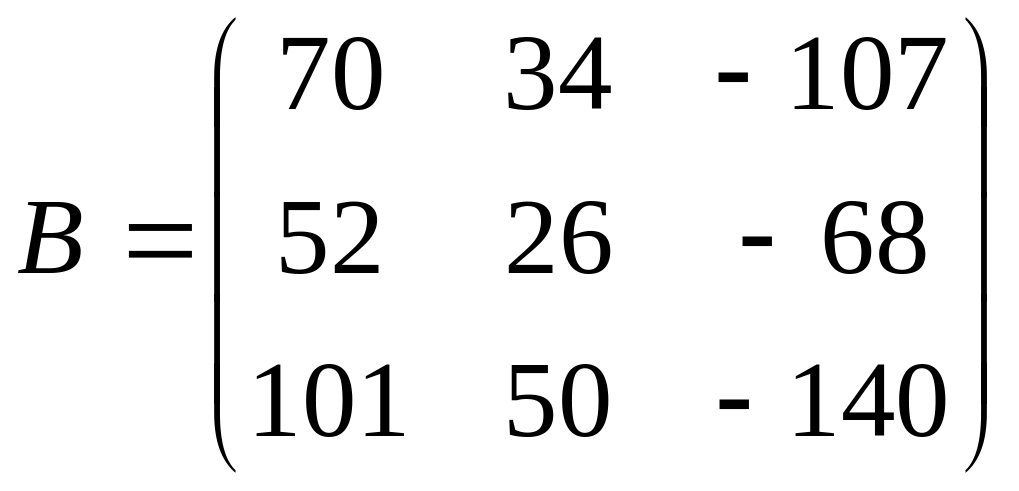 ;
;
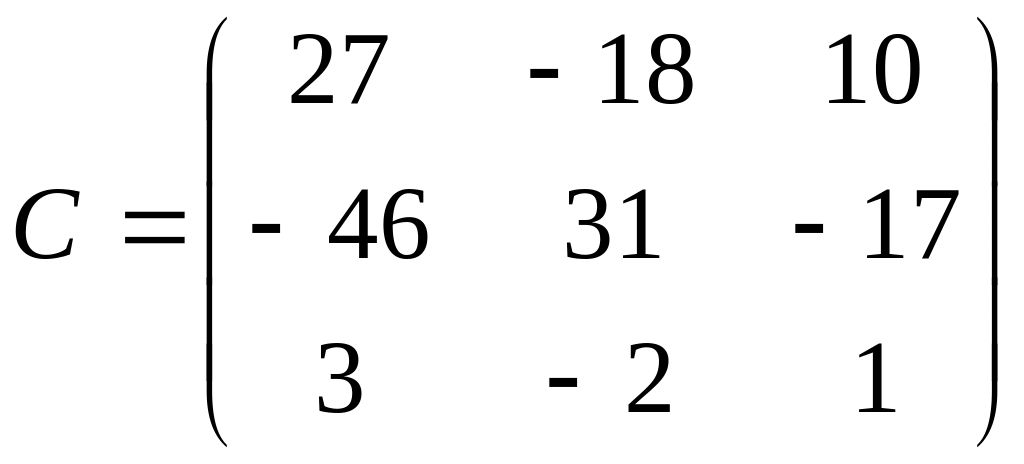 .
.
Яку матрицю D потрібно додати до матриці АВС, щоб дістати одиничну матрицю? Чому дорівнює визначник матриці АВС.
Розв’язати матричне рівняння АХ=В, якщо
 ;
;
 .
.
Зробити перевірку.
Розв’язати систему лінійних рівнянь a) за формулами Крамера;
б) матричним методом.
![]()
Дослідити на сумісність систему використовуючи метод Гаусса:
![]()
Знайти ранг матриці .
Варіант 19
Обчислити визначник
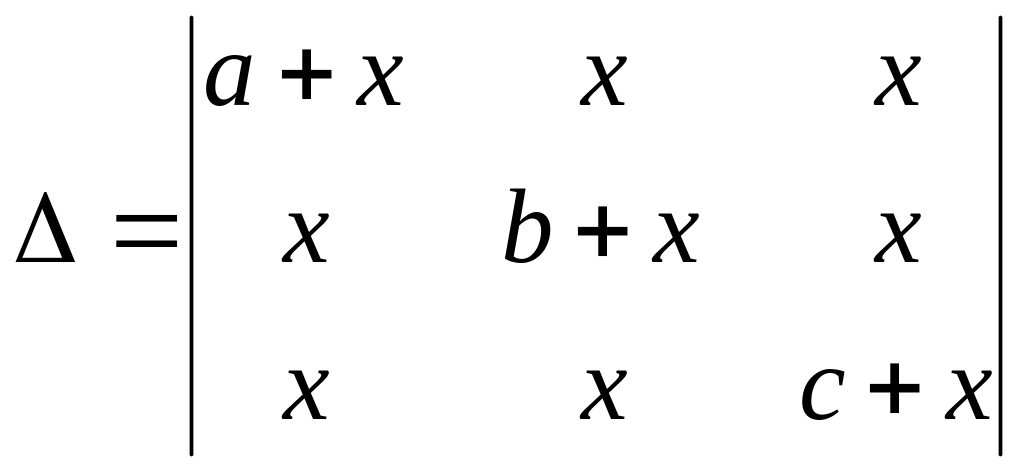 .
.
Вказівка. 1-ий спосіб. Зобразити визначник так:
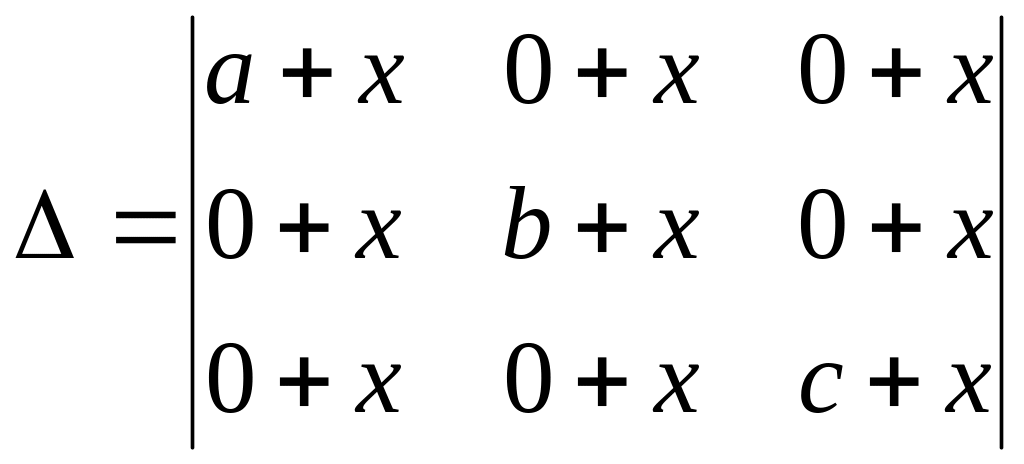 .
.
Далі скористатися лінійною властивістю визначників.
2-ий спосіб. Іс–ІІс; ІІс–ІІІс.
Обчислити визначник накопиченням нулів у рядку чи у стовпці.
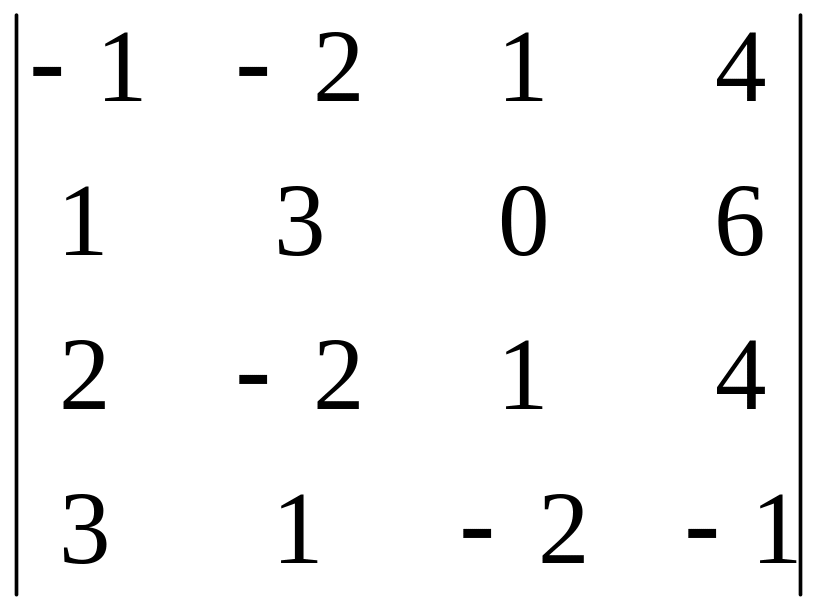 .
.
Задана матриця
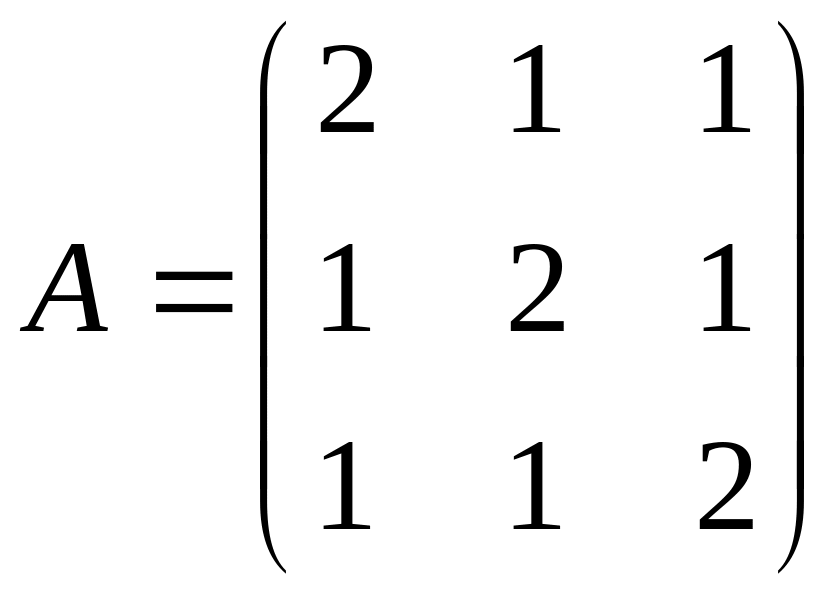 .
.
Знайти суму матриць А2+А+Е, де Е – одинична матриця 3-го порядку.
Довести, що матриця А – ортогональна, якщо
 .
.
Зауваження. Квадратна матриця А називається ортогональною, якщо виконується умова ААТ=Е, або АТ=А–1.
Знайти невідому матрицю Х із рівняння
![]() .
.
Зробити перевірку.
Розв’язати систему лінійних рівнянь а) за допомогою формул Крамера;
б) матричним методом.
![]()
Дослідити на сумісність систему використовуючи метод Гаусса:
![]() .
.
Знайти ранг матриці .
Варіант 20
Користуючись властивостями визначників, обчислити визначник
 .
.
Обчислити визначник, розклавши його за елементами 1-го рядка.

Знайти значення многочлена

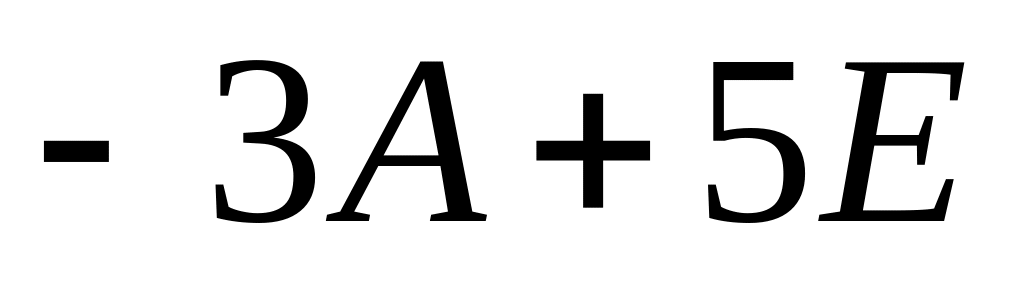 ,
якщо
,
якщо
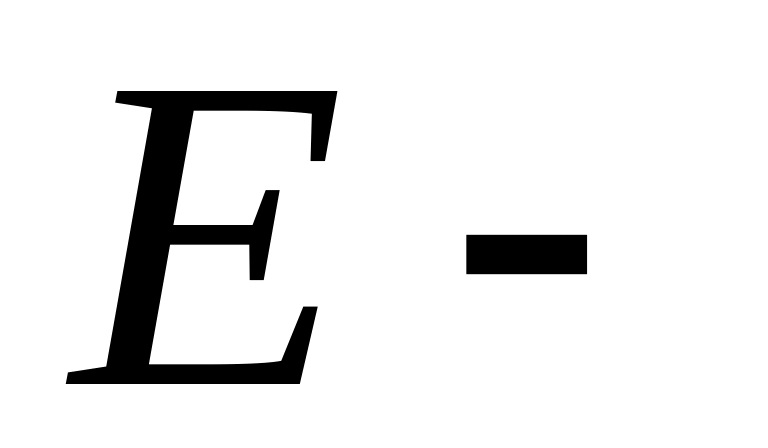 одинична
матриця 3-го порядку,
одинична
матриця 3-го порядку,
![]()
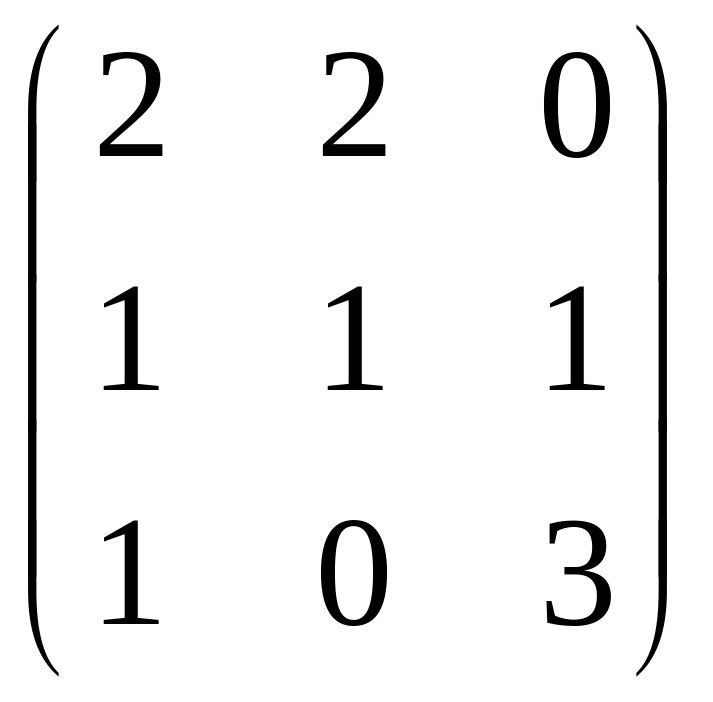 .
.
Знайти добуток матриць
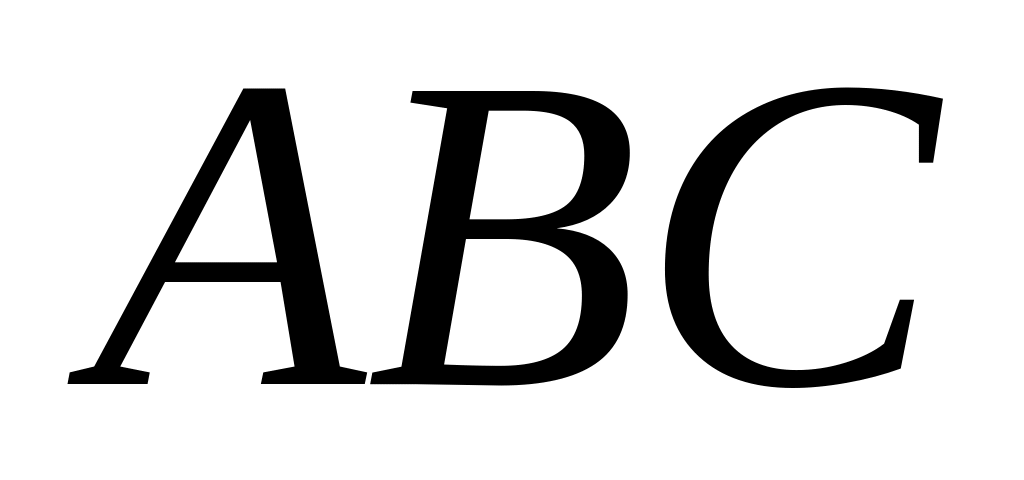 ,
якщо
,
якщо
![]() ;
; ![]()
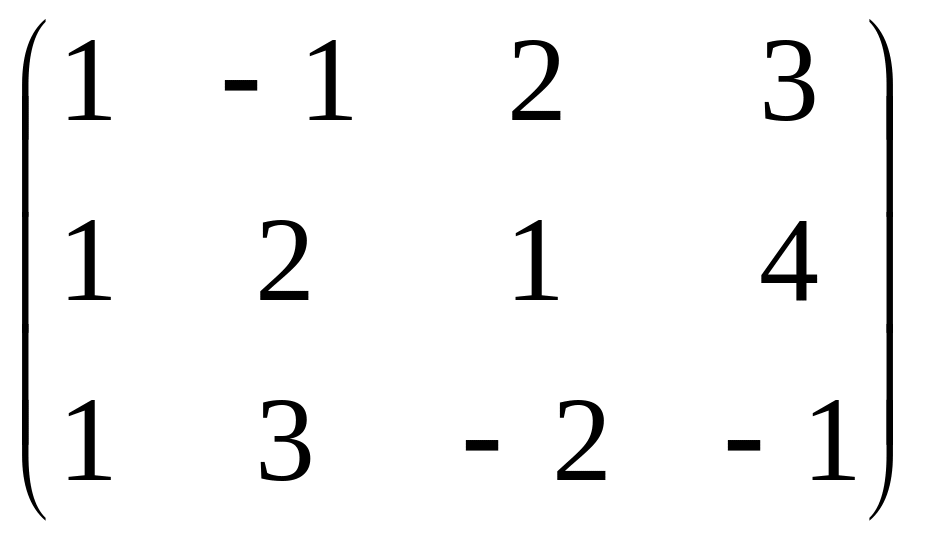 ;
; ![]()
 .
.
Переконатися,
що
![]() .
.
Знайти невідому матрицю
 із
рівняння
із
рівняння
![]()
![]()
![]() =
=![]() .
.
Зробити перевірку.
Розв’язати систему лінійних рівнянь a) за формулами Крамера;
б) матричним методом.
![]()
Дослідити на сумісність систему використовуючи метод Гаусса:
![]() .
.
Знайти ранг матриці
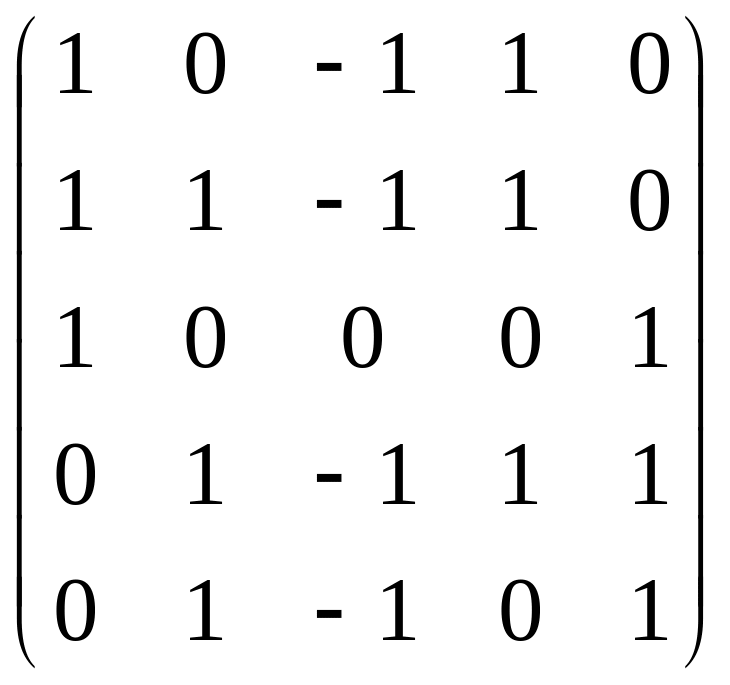 .
.
Варіант 21
Розв’язати рівняння, зробити перевірку.
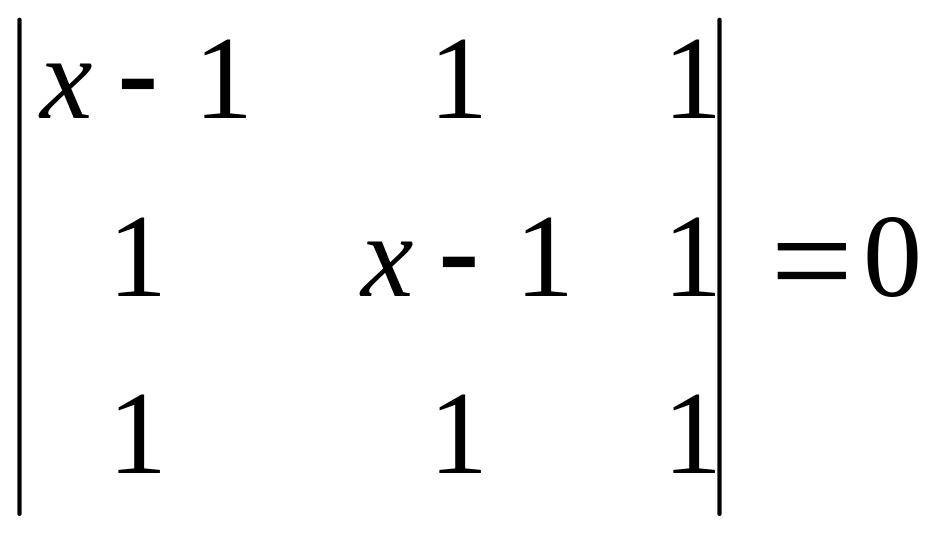 .
.
Обчислити визначник, розклавши його за елементами 2-го стовпця.
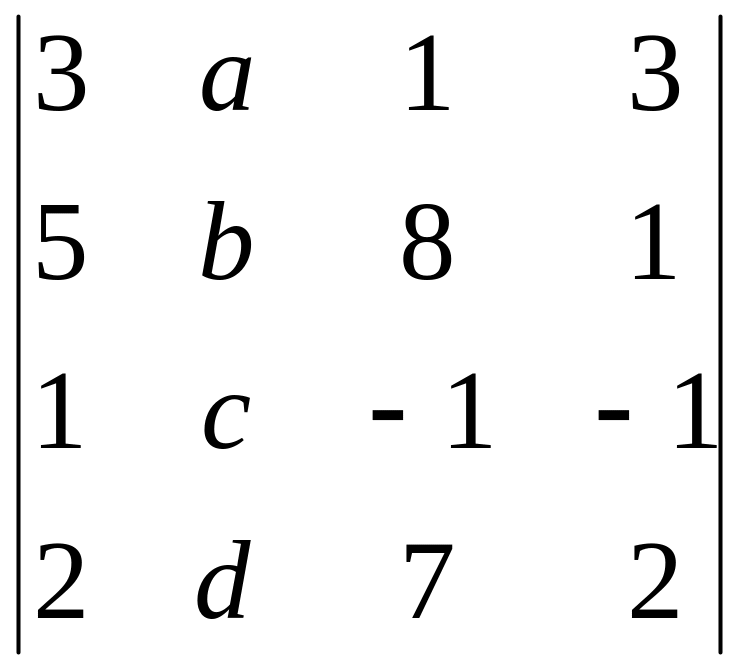
Знайти значення многочлена від матриці f(A)=3A2-2A+5E, якщо E-одинична матриця 3-го порядку,
A= .
.
Нехай
A= ;
В=
;
В= .
.
Знайти АВ; ВА та ВВТ. Коли операція множення матриць неможлива, пояснити чому.
Розв’язати матричне рівняння YA=B, якщо
А= ;
B=
;
B= .
.
Зробити перевірку.
Розв’язати систему лінійних рівнянь
![]()
а)користуючись формулами Крамера;
б) матричним методом.
Розв’язати однорідну систему рівнянь:
![]() .
.
Знайти ранг матриці
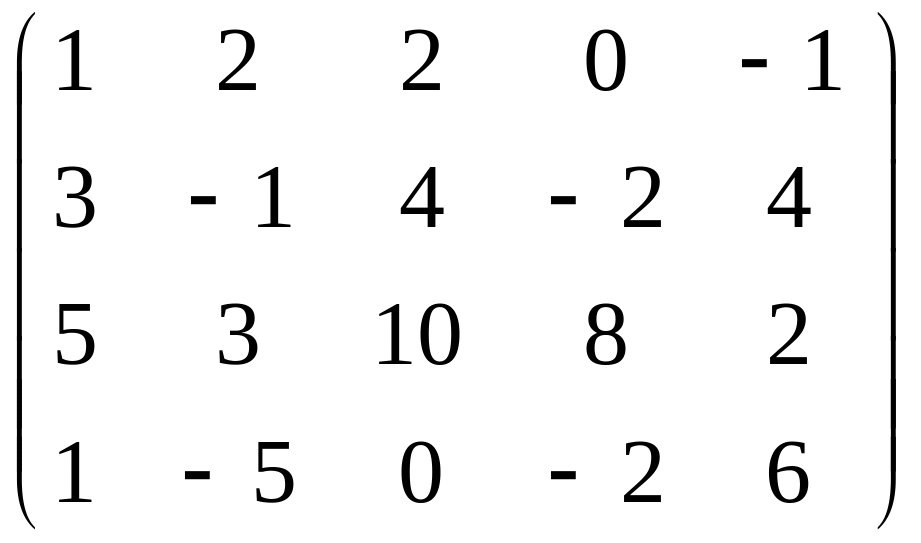 .
.
Варіант 22
Користуючись властивостями визначників, обчислити визначник
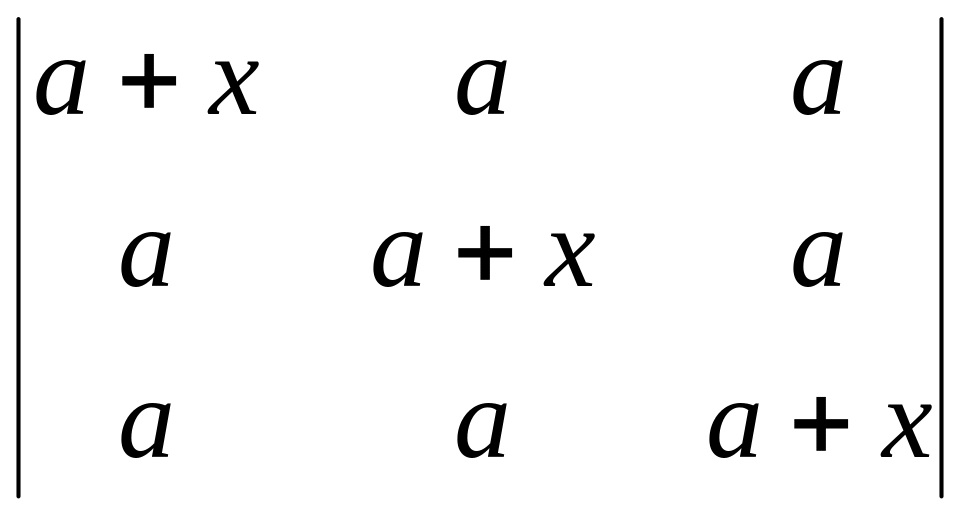 .
.
Вказівка. Іс.–ІІс.; ІІс.–ІІІс..
Обчислити визначник, розклавши його за елементами того рядка, який містить найбільшу кількість нулів
 .
.
Знайти
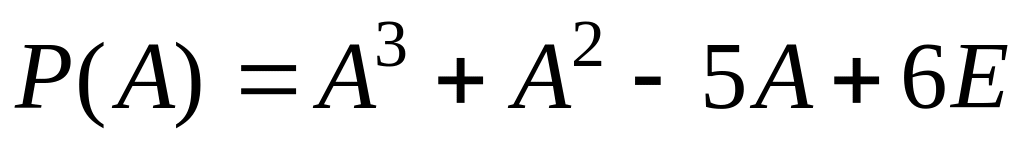 ,
якщо Е
– одинична матриця 2-го порядку,
,
якщо Е
– одинична матриця 2-го порядку,
![]() .
.
Задано матриці
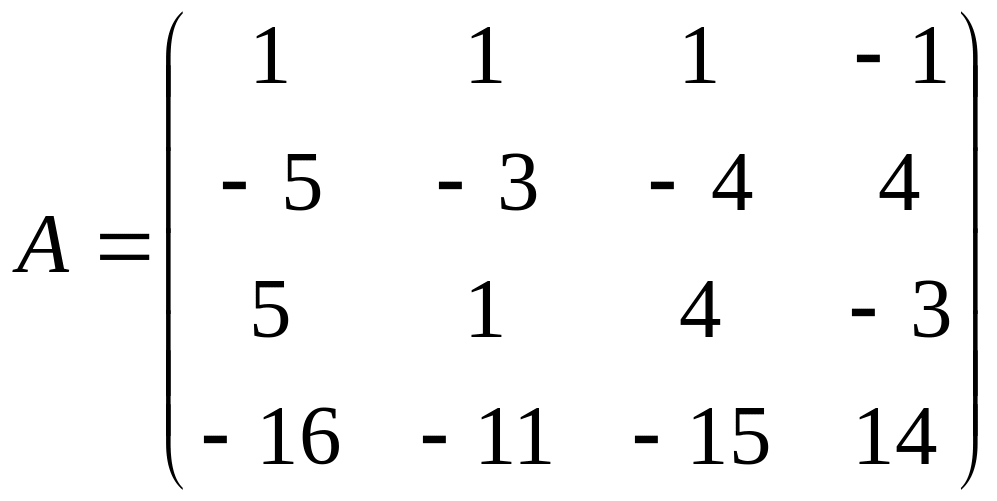 ;
;
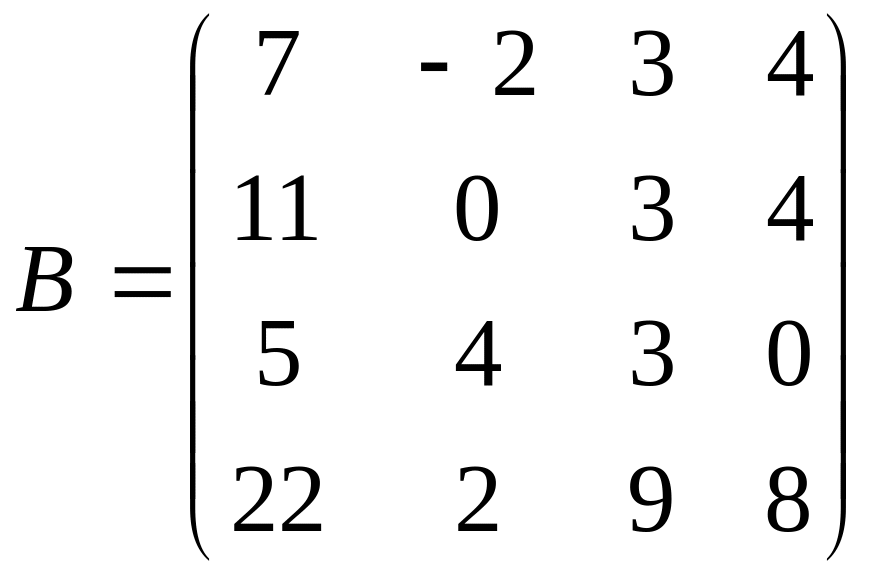 .
.
а). Знайти добуток матриць АВ.
б). Обчислити визначник матриці АВ.
Розв’язати матричне рівняння АХ=В, якщо
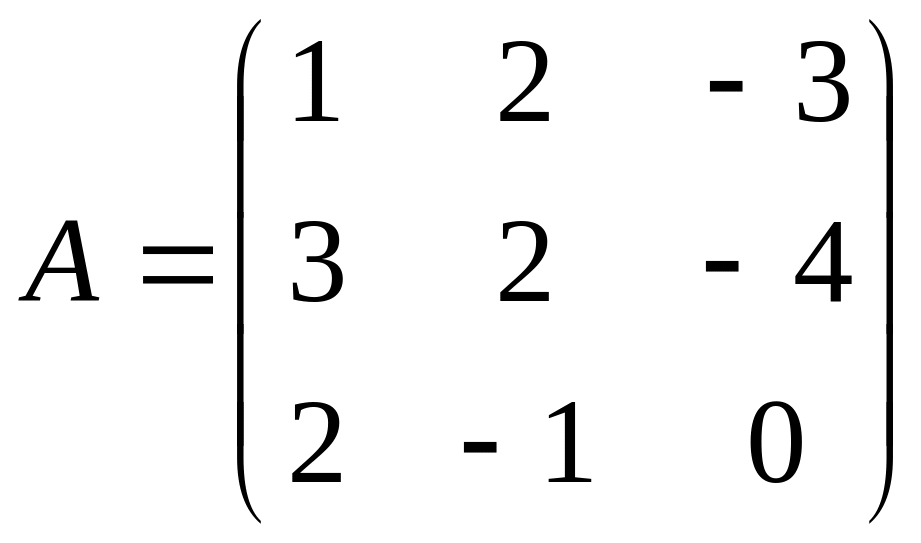 ;
;
 .
.
Зробити перевірку.
Розв’язати систему лінійних рівнянь a) за формулами Крамера;
б) матричним методом.
![]()
Визначити, при яких значеннях а та b система рівнянь a) має єдиний розв’язок (визначена); б) не має розв’язків (несумісна).
![]()
Знайти ранг матриці .
Варіант 23
Користуючись властивостями визначників, спочатку спростити, а потім обчислити визначник
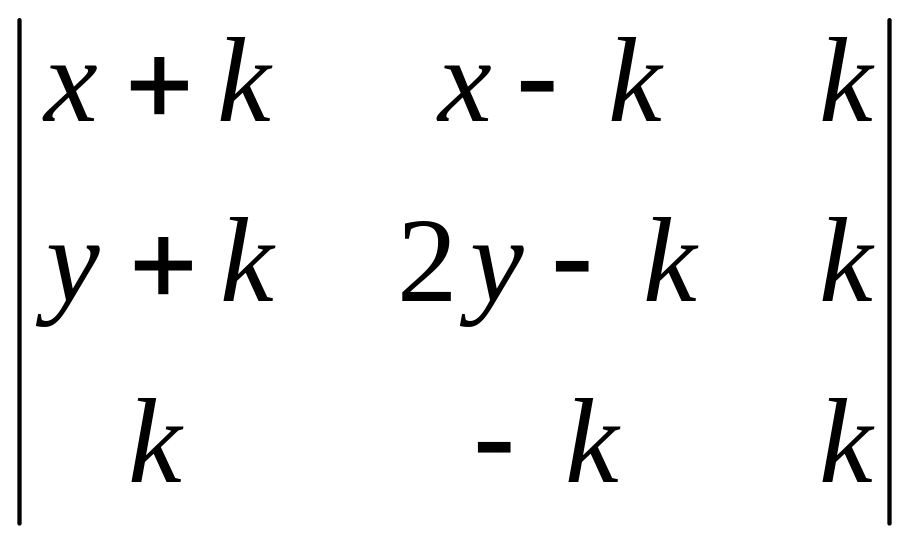 .
.
Обчислити визначник
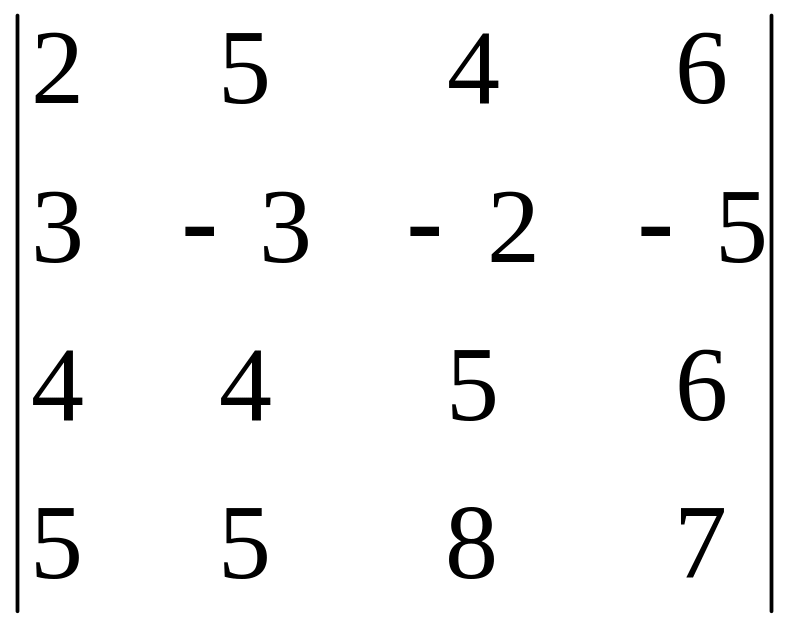 .
.
Знайти
 ,
якщо
Е
– одинична матриця 3-го порядку,
,
якщо
Е
– одинична матриця 3-го порядку,
 .
.
Нехай
![]() ;
;
 .
.
а) Знайти АВ; ВА; ААТ.
Якщо операція множення матриць у деяких випадках неможлива, пояснити чому.
б) Обчислити визначник матриці ААТ.
Розв’язати матричне рівняння відносно квадратної матриці 3-го порядку АХ=В, якщо
 ;
;
 .
.
Зробити перевірку.
Розв’язати систему лінійних рівнянь a) за формулами Крамера;
б) матричним методом.
![]()
Розв’язати систему рівнянь методом Гаусса:
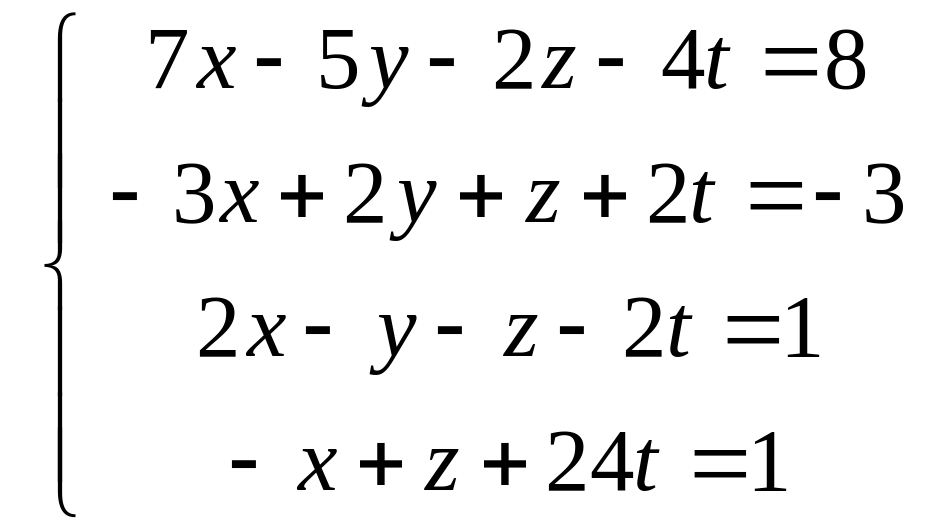 .
.
Знайти ранг матриці .
Варіант 24
Користуючись властивостями визначників, довести тотожність
 .
.
Вказівка.
1-ий спосіб. У визначнику, що стоїть
ліворуч, 1-ий рядок помножити на а;
2-ий – на b;
3-ій – на с.
Весь визначник помножити на
![]() (припускаємо, що а,
b
та
с
≠0).
(припускаємо, що а,
b
та
с
≠0).
2-ий
спосіб. До 3-го стовпця визначника, що
стоїть ліворуч, додати 2-ий стовпець,
попередньо помноживши його на
![]() ,
і відняти 1-ий стовпець, помножений на
,
і відняти 1-ий стовпець, помножений на
![]()
Розв’язати рівняння, ліва частина якого записана у вигляді визначника:
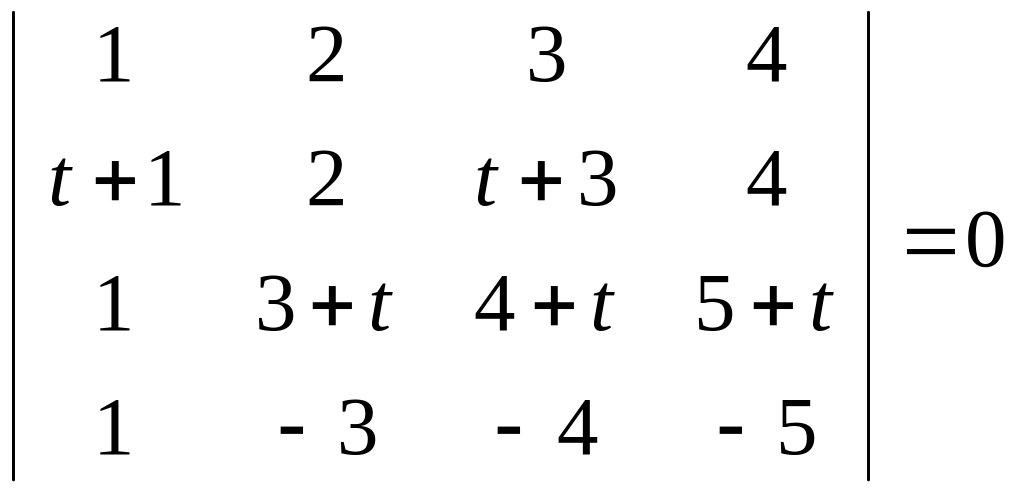 .
.
Вказівка. ІІр-Ір; ІІІр-Ір. Із 2-го та 3-го рядків винести за знак визначника спільний множник t та 1+t відповідно.
Знайти
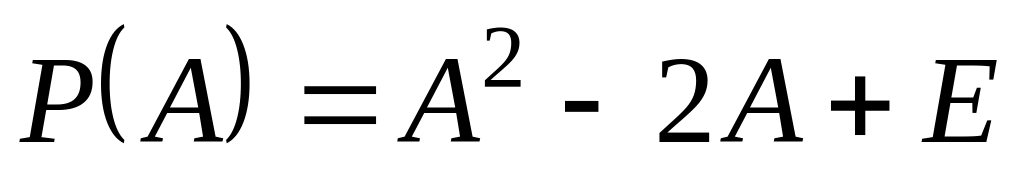 ,
якщо E
– одинична
матриця 3-го порядку,
,
якщо E
– одинична
матриця 3-го порядку,
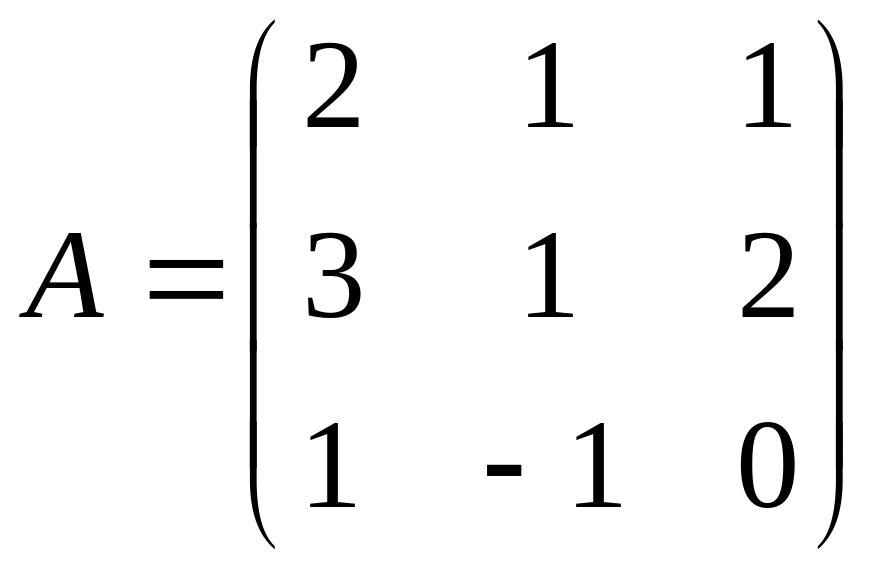 .
.
Знайти добутки AB та BA, якщо
A=![]()
![]() ,
B=
,
B= .
.
Яку матрицю C потрібно додати до матриці BA, щоб дістати одиничну матрицю?
Розв’язати матричне рівняння відносно квадратної матриці X 3-го порядку AX=B, якщо
A= ;
B=
;
B=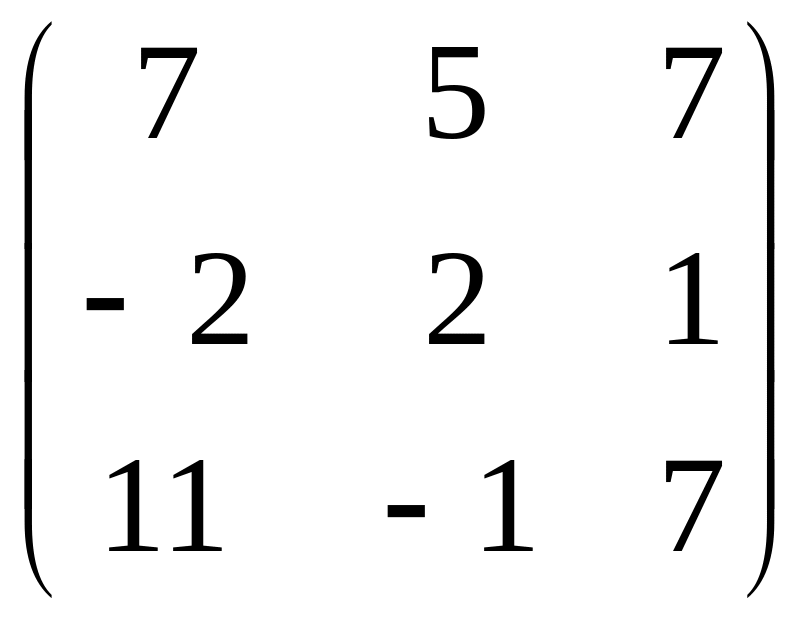 .
.
Зробити перевірку.
Розв’язати систему лінійних рівнянь а) за допомогою формул Крамера;
б) матричним методом.
![]()
