
- •Математика Алгебра та початки аналізу Частина іі
- •Харків 2012
- •Розділ 1 Тригонометричні функції числового аргументу
- •§2 Тригонометричні функції числового аргументу
- •§3 Властивості тригонометричних функцій
- •§4 Основні тригонометричні тотожності
- •§5 Формули зведення
- •§6 Основні формули тригонометрії
- •§7 Властивості та графіки тригонометричних функцій Властивості та графік функції
- •Властивості та графік функції
- •Властивості та графік функції
- •Властивості та графік функції
- •§8 Обернені тригонометричні функції
- •§9 Розв’язання найпростіших тригонометричних рівнянь
- •§ 10 Розв’язання тригонометричних рівнянь
- •§ 11 Розв’язання тригонометричних нерівностей
- •Розділ 2 Похідна функції та її застосування
- •§ 12 Приріст функції в точці. Похідна функції та її механічний зміст
- •§ 13 Похідна степеневої функції
- •§14 Похідна суми, різниці, добутку та частки двох функцій Правила диференціювання
- •§15 Похідна складеної функції
- •§ 16 Похідні тригонометричних функцій
- •§ 17 Похідна показникової функції
- •§ 18 Похідна логарифмічної функції
- •§ 19 Геометричний зміст похідної
- •§ 20 Похідні вищих порядків
- •§ 21 Диференціал функції і його застосування до наближених обчислень
- •§ 22 Ознака сталості, зростання та спадання функції
- •§ 23 Екстремум функції
- •§ 24 Побудова графіків функцій Загальна схема для побудови графіків функцій
- •§ 25 Найменше та найбільше значення функції
- •Розділ 3 Інтеграл та його застосування
- •§ 26 Первісна функції. Невизначений інтеграл та його властивості
- •Основні властивості невизначених інтегралів
- •Основні формули інтегрування
- •§ 27 Визначений інтеграл та його властивості
- •Основні властивості визначеного інтегралу:
- •§ 28 Площа криволінійної трапеції
- •§ 29 Застосування визначеного інтеграла при розв’язанні фізичних задач
- •Розділ 4 Елементи теорії ймовірностей і математичної статистики
- •§ 30 Елементи комбінаторики
- •§ 31 Основні поняття теорії ймовірностей
- •§ 32 Операції над подіями. Теореми про додавання і множення ймовірностей
- •§ 33 Дискретні випадкові величини
- •§ 34 Вступ до статистики
- •Список літератури
§ 28 Площа криволінійної трапеції
К риволінійною
трапецією називається
фігура, обмежена графіком неперервної
функції
риволінійною
трапецією називається
фігура, обмежена графіком неперервної
функції
![]() ,
яка невід’ємна на відрізку
,
прямими
,
яка невід’ємна на відрізку
,
прямими
![]() ,
,
![]() і
віссю ОХ.
і
віссю ОХ.
Рис. 9
Площа криволінійної
трапеції дорівнює визначеному інтегралу
від заданої функції на заданому
відрізку:
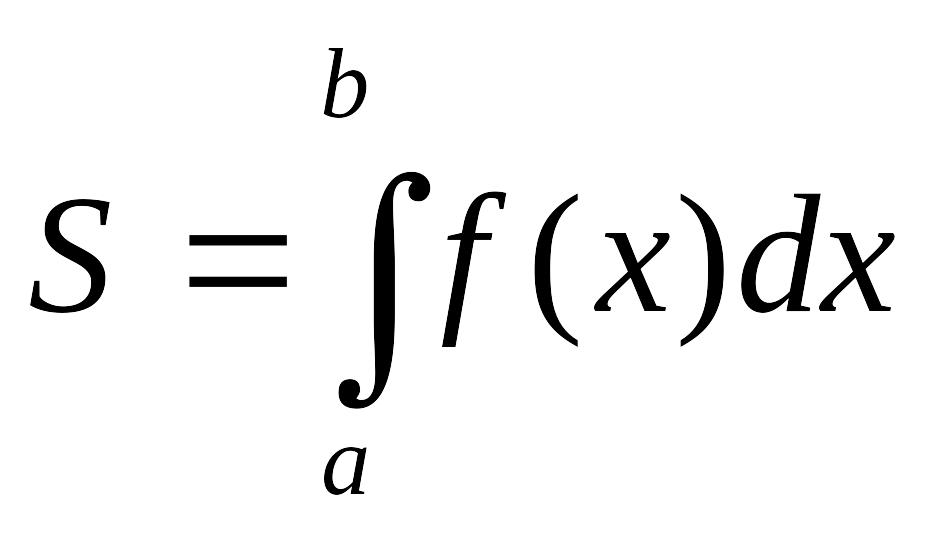 .
.
157. Обчисліть визначені інтеграли і побудувати схематично фігури, площі яких виражаються цими інтегралами:
1)
; 2)
![]() ;
;
3)
 ; 4)
; 4)
![]() .
.
158. Запишіть за допомогою інтегралу площі фігур, зображених на рисунку:
А) Б) В)


 Рис.
10
Рис.
10
159. Знайдіть площу фігури, обмежену:
1) параболою
![]() та прямими
та прямими
![]() ,
,
![]() ,
,
![]() ;
;
2) параболою
та прямими
,
![]() ,
,
![]() ;
;
3) графіком функції
![]() та прямими
,
та прямими
,![]() ;
;
4) графіком функції
![]() та прямими
,
;
та прямими
,
;
5) графіком функції
![]() та прямими
,
та прямими
,
![]() ,
,
![]() ;
;
6) графіком функції
![]() та прямими
,
та прямими
,
![]() ,
,
![]() ;
;
7) параболою
![]() та віссю абсцис;
та віссю абсцис;
8) параболою
![]() та віссю абсцис;
та віссю абсцис;
9) параболою
![]() ,
віссю абсцис та прямою
,
віссю абсцис та прямою
![]() ;
;
10) параболою
![]() ,
віссю абсцис та прямою
,
віссю абсцис та прямою
![]() ;
;
11) графіком функції
![]() та прямими
,
,
та прямими
,
,
![]() ;
;
12) графіком функції та прямими , , ;
13) графіком функції
![]() та прямими
,
та прямими
,
![]() ;
;
14) графіком функції
![]() та прямими
,
та прямими
,
![]() ;
;
15) графіком функції
![]() та прямими
,
та прямими
,
![]() ,
,
![]() ;
;
16) графіком функції
![]() та прямими
,
,
та прямими
,
,
![]() ;
;
17) графіком функції
![]() та прямими
,
,
;
та прямими
,
,
;
18) графіком функції
![]() та прямими
,
,
;
та прямими
,
,
;
19) графіком функції
![]() та прямими
,
,
;
та прямими
,
,
;
20) графіком функції
![]() та прямими
,
,
;
та прямими
,
,
;
21) графіком функції
![]() та
прямими
,
,
;
та
прямими
,
,
;
22)
графіком
функції
та
прямими
,
![]() ,
;
,
;
23)
графіками
рівнянь
![]() ,
,
![]() та
;
та
;
24) графіками рівнянь
![]() ,
,
![]() та
;
та
;
160. Знайдіть площу фігури, обмежену:
1) параболою
![]() та прямою
та прямою
![]() ;
;
2)параболою
![]() та прямою
та прямою
![]() ;
;
3) параболою
та прямою
![]() ;
;
4) параболою
та прямою
![]() ;
;
5) параболою
![]() ,
прямою
та віссю ординат;
,
прямою
та віссю ординат;
6) параболою
![]() ,
прямою
,
прямою
![]() та віссю ординат;
та віссю ординат;
7) параболою
![]() та прямою
та прямою
![]() ;
;
8) параболою
![]() та прямою
та прямою
![]() ;
;
9) графіком функції
![]() та прямими
,
;
та прямими
,
;
10) графіком функції
![]() та прямими
,
;
та прямими
,
;
11) графіком функції та прямими , ;
12) графіком функції
![]() та прямими
,
та прямими
,
![]() ;
;
13) графіком функції
![]() та прямими
,
;
та прямими
,
;
14) графіком функції
![]() та прямими
,
;
та прямими
,
;
15) графіком функції
![]() та прямими,
,
;
та прямими,
,
;
16) графіком функції
![]() та прямими,
та прямими,
![]() ,
;
,
;
17) графіком функції
![]() та прямою
та прямою
![]() ;
;
18) графіком функції
та прямою
![]() ;
;
19) графіком функції
![]() та прямими
та прямими
![]() ,
;
,
;
20)графіком функції
та прямими
![]() ,
;
,
;
21) графіками функцій
та
![]() ;
;
22)графіками функцій
та
![]() ;
;
23) параболою
![]() та прямою
та прямою
![]() ;
;
24) параболою
![]() та прямою
та прямою
![]() ;
;
25) параболами
![]() та
;
та
;
26) параболами та ;
27) графіками функцій
![]() ,
,
![]() та прямою
;
та прямою
;
28) графіками функцій
![]() ,
,
![]() та прямою
;
та прямою
;
29) графіками функцій , та прямою ;
30) графіками функцій , та прямою ;
31) графіками функцій , та прямою ;
32) графіками функцій
![]() ,
та прямою
,
та прямою
![]() ;
;
33) графіком функції
![]() та прямими
,
;
та прямими
,
;
34) графіком функції
![]() та прямими
,
та прямими
,
![]() ;
;
35) графіками функцій
![]() та
та
![]() ;
;
36) графіками функцій
та
![]() .
.
161. Знайдіть площі фігур, обмежені:
1) графіками функцій
,
![]() і віссю абсцис;
і віссю абсцис;
2)
графіками
функцій
![]() ,
,
![]() і віссю абсцис;
і віссю абсцис;
3) графіком функції
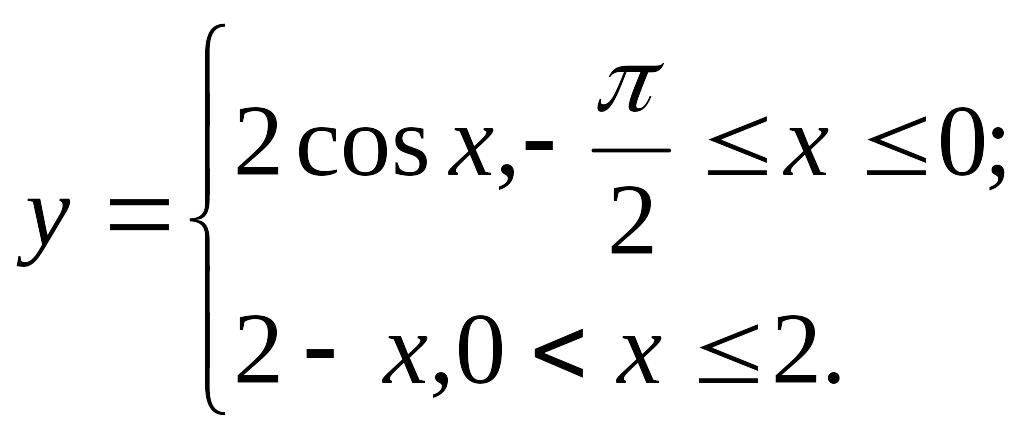 і
віссю абсцис;
і
віссю абсцис;
4) графіком функції
 і віссю абсцис;
і віссю абсцис;
5) графіками функцій
,
![]() та віссю абсцис;
та віссю абсцис;
6) графіками функцій
,
![]() та віссю абсцис.
та віссю абсцис.
162. Використовуючи геометричний зміст інтегралу, обчисліть:
1)
![]() ; 2)
; 2)
 ;
;
3)
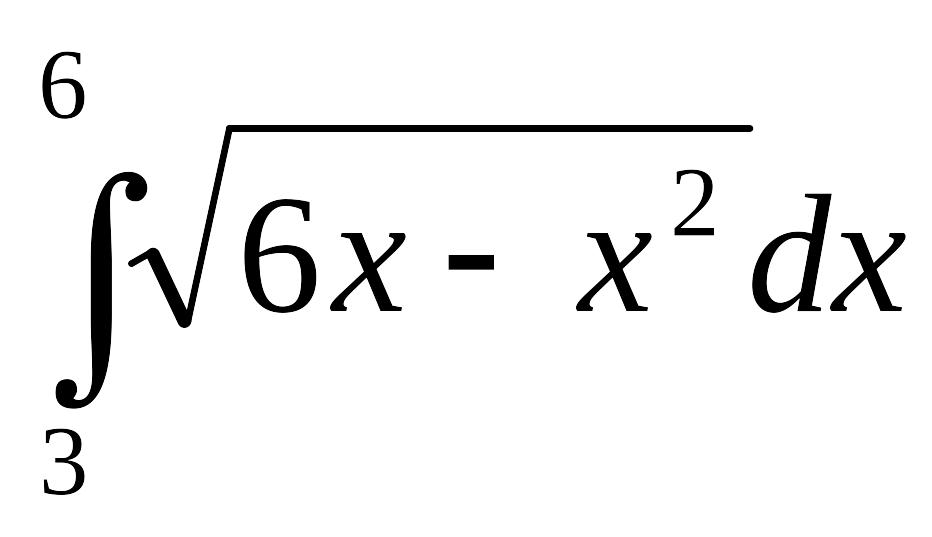 ; 4)
; 4)
 ;
;
5)
 ; 6)
; 6)
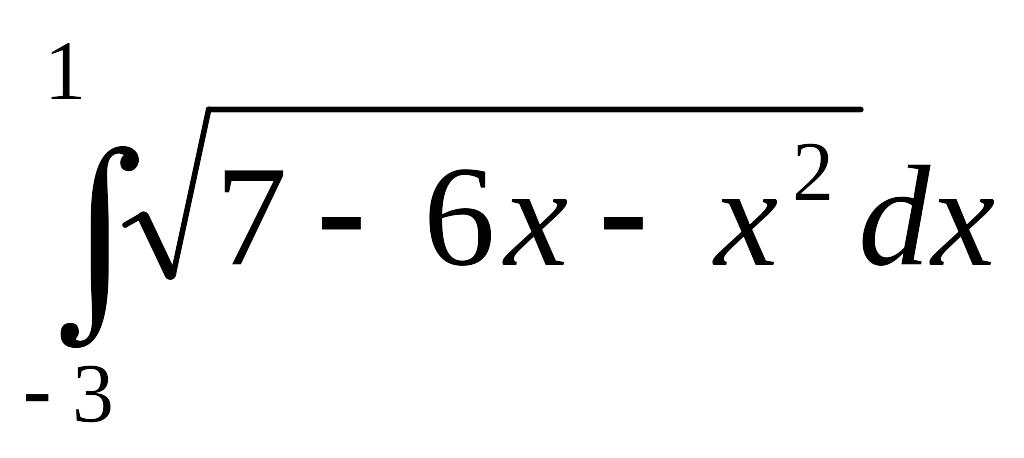 .
.
163. Знайдіть
площу фігури, обмеженої параболою
![]() ,
дотичною, проведеною до цієї параболи
в точці з абсцисою
,
дотичною, проведеною до цієї параболи
в точці з абсцисою
![]() ,
та віссю ординат.
,
та віссю ординат.
164. Знайдіть,
при якому значенні
площа фігури, обмеженої параболою
![]() та прямими
,
та прямими
,
![]() ,
,
![]() буде приймати найменше значення.
буде приймати найменше значення.
165. Знайдіть
площу фігури, обмежену графіками функцій
![]() та
та
![]() .
.
до змісту
