6.7 Фильтрационные расчеты

Фильтрационными расчетами следует определять: положение фильтра­ционной поверхности потока (депрессионной кривой) в теле плотины и бере­гах; фильтрационный расход воды через тело плотины, основания и берега, на­поры (или градиенты) фильтрационного потока в теле плотины и основания, а также в местах выхода в дренаж.

Однородные плотины на водонепроницаемом основании

1. Плотина без дренажа

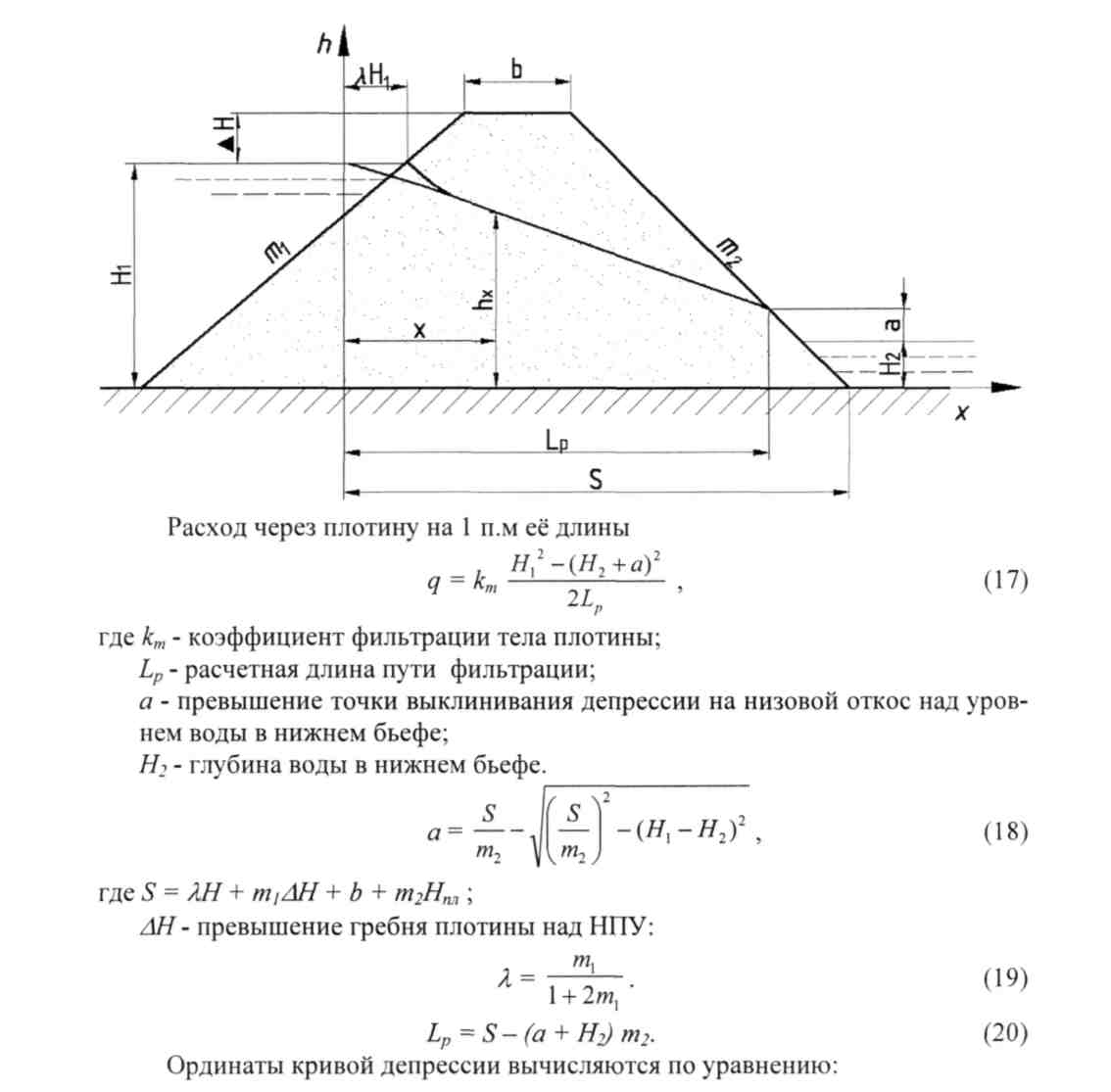
Расход на 1 п.м её длины

где

k_m-коэффициент фильтрации тела плотины;

L_p-расчетная длина пути фильтрации;

a-превышение точки выклинивания депрессии на низовой откос над уровнем воды в нижнем бьефе.

Н₂-глубина воды в нижнем бьефе.

где S=λH+m₁ΔH+b+m₂H_пл;

ΔH-превышение гребня плотины над НПУ:

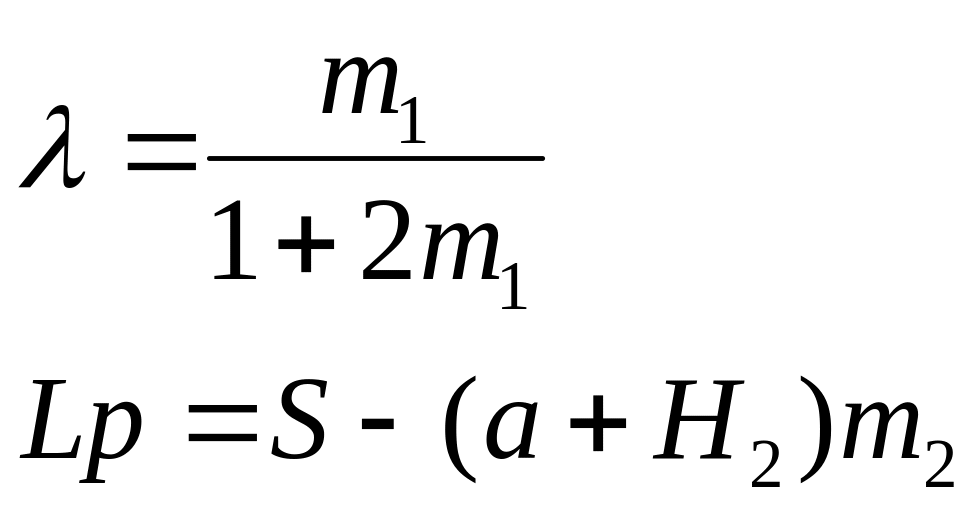
Ординаты кривой депрессии вычисляют по уравнению:

3. Плотина с трубчатым дренажом

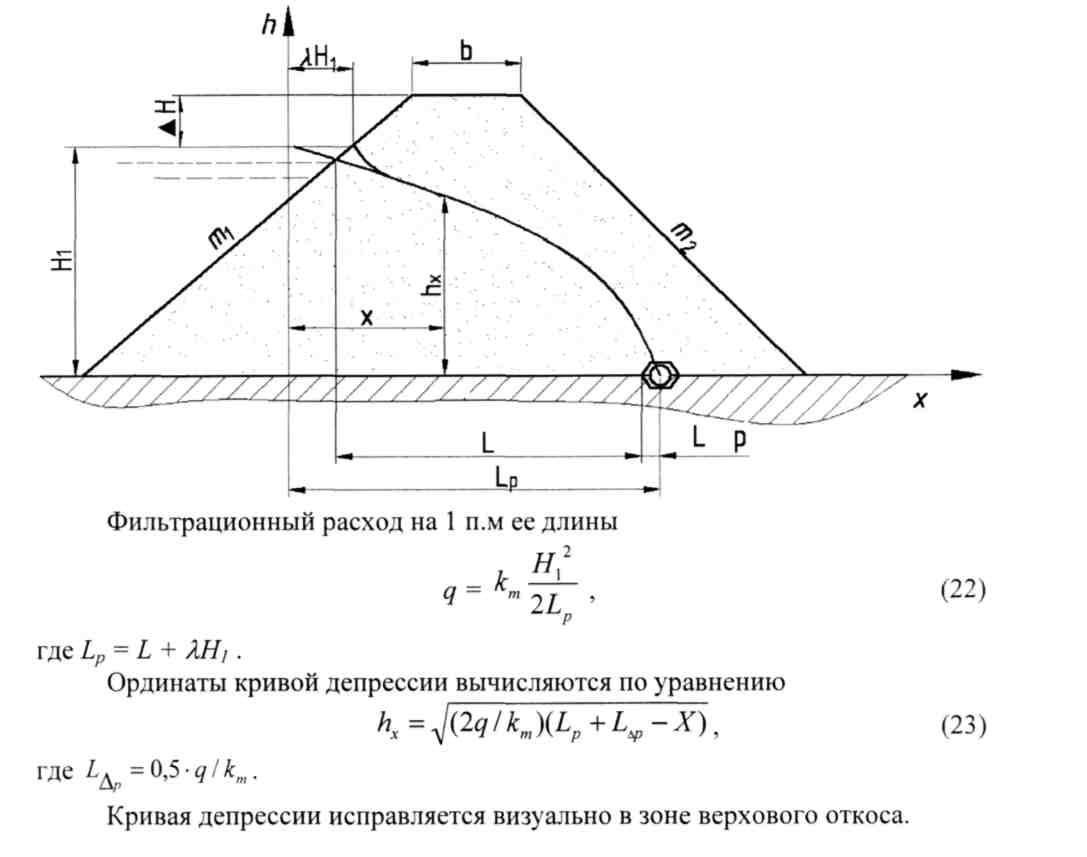
Фильтрационный расход на 1 п.м её длины

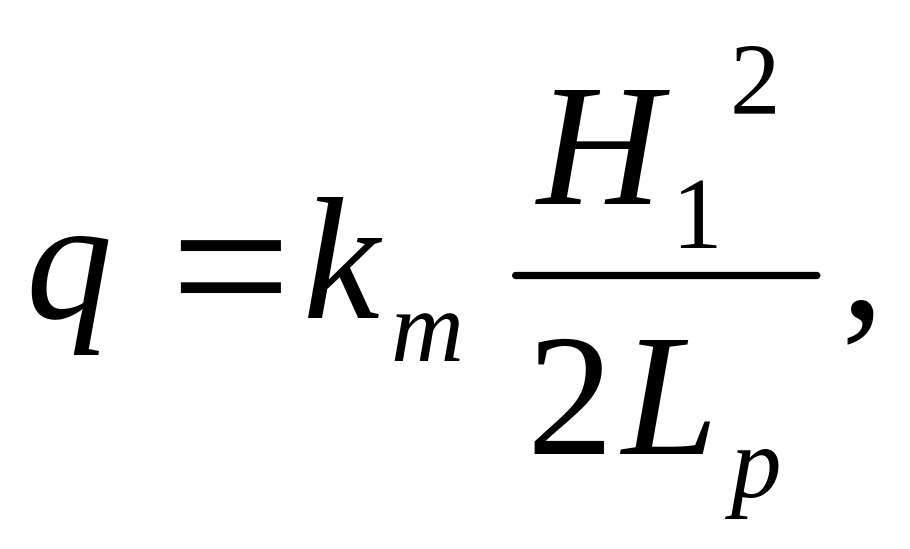
Где L_p=L+λH₁

Ординаты кривой депрессии вычисляются по уравнению

где

Кривая депрессии исправляется визуально в зоне откоса.

3. Плотина с дренажной призмой

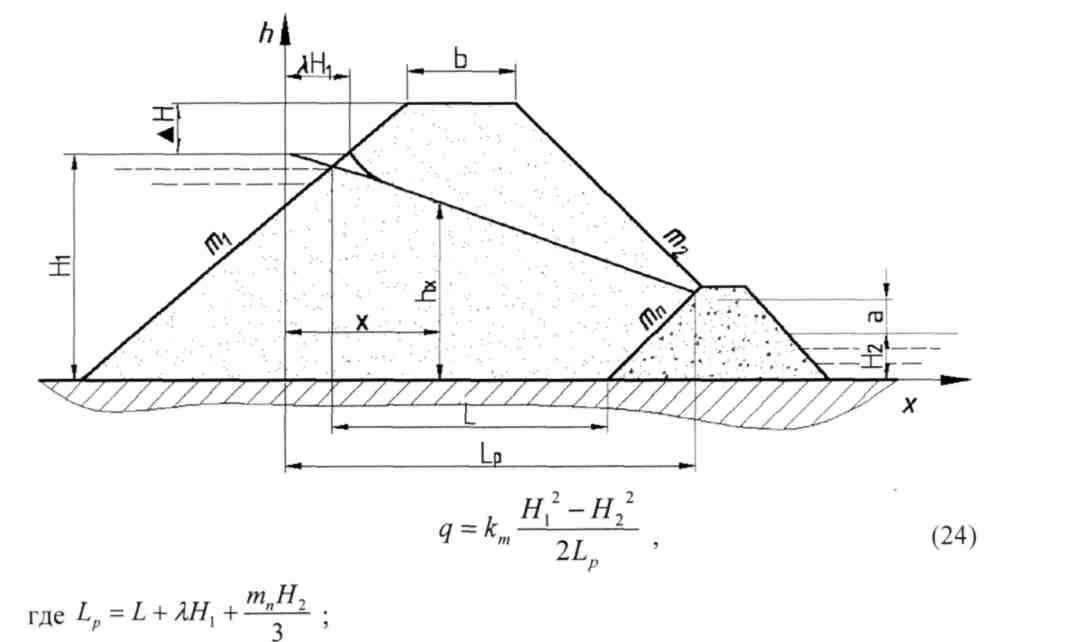
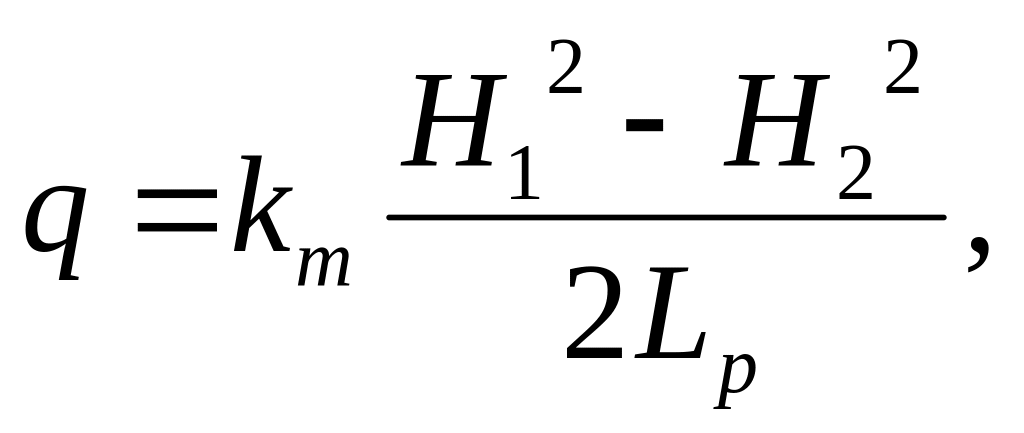
При L_p=L+λH₁+m_nH₂/3;

т_п - коэффициент внутреннего откоса дренажной призмы. Превышение точки выклинивания кривой депрессии над уровнем воды в нижнем бьефе на внутренний откос дренажной призмы определяется

где/C/nJ принимается в зависимости от т_п.

т„	0	0,5	1	1,5	2	2,5
f(m,J	0,74	0,51	0,36	0,28	0,22	0,18

Ординаты кривой депрессии вычисляются по уравнению

Кривая депрессии исправляется визуально в зоне верхнего откоса.

4. Плотина с наклонным дренажом при отсутствии воды в нижнем бьефе

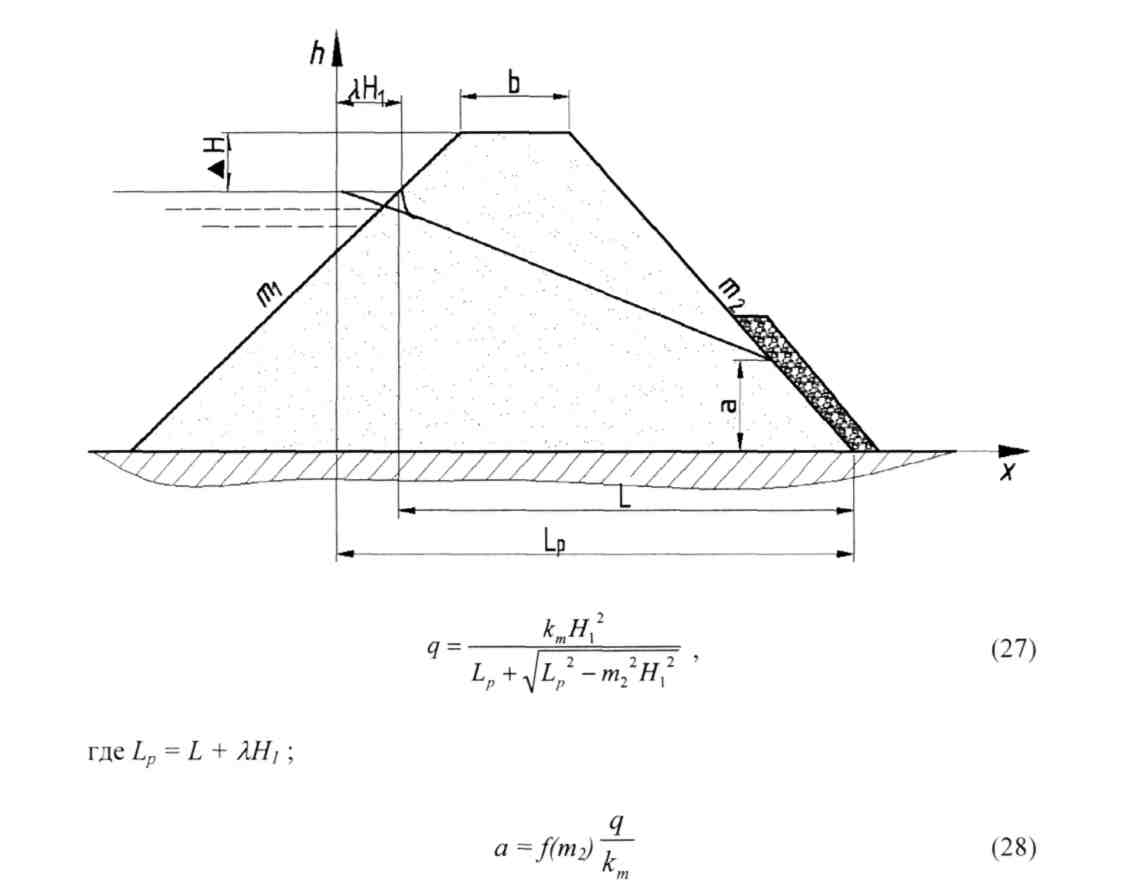
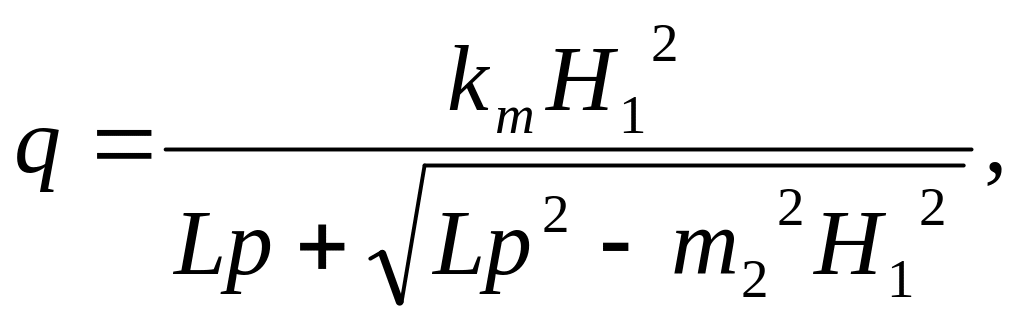
Где L_p=L+λH₁

при т₂ > 1 значение f(m₂) = 0,51 + т₂, при т₂ < 1 значение f(m₂) = 0,7 + 0,8 т₂.

Кривая депрессии строится по уравнению

Кривая депрессии исправляется визуально в зоне, где h_x≥H_}-q/k_m .

5. Плотина с наклонным дренажом при наличии воды в нижнем бьефе

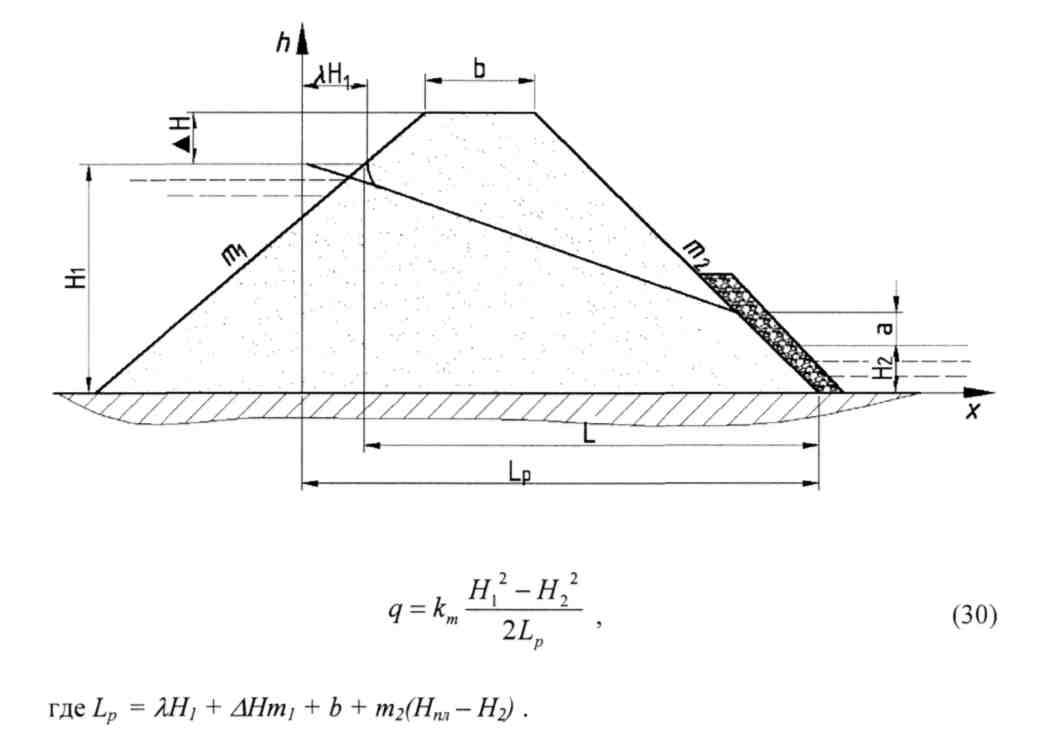
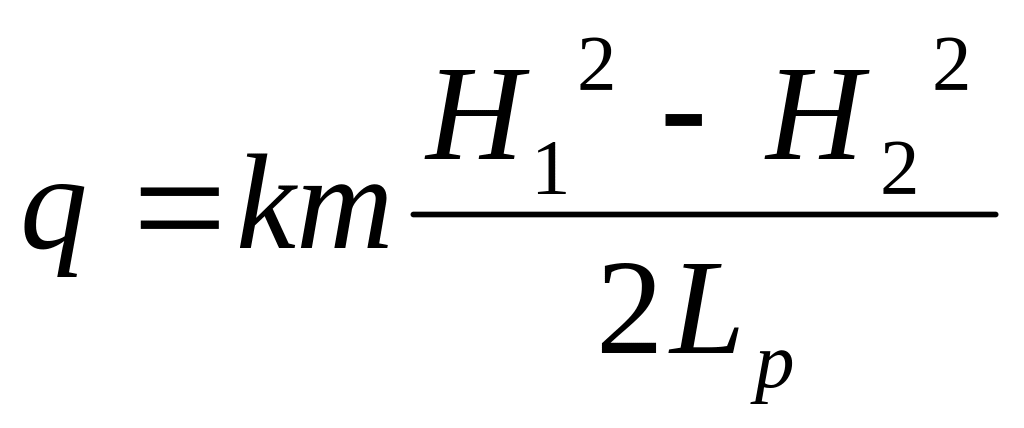
Где L_p=λH₁+ΔH_m1+b+m₂(H_пл-H₂)

Выклинивание кривой депрессии выше уровня воды в нижнем бьефе а

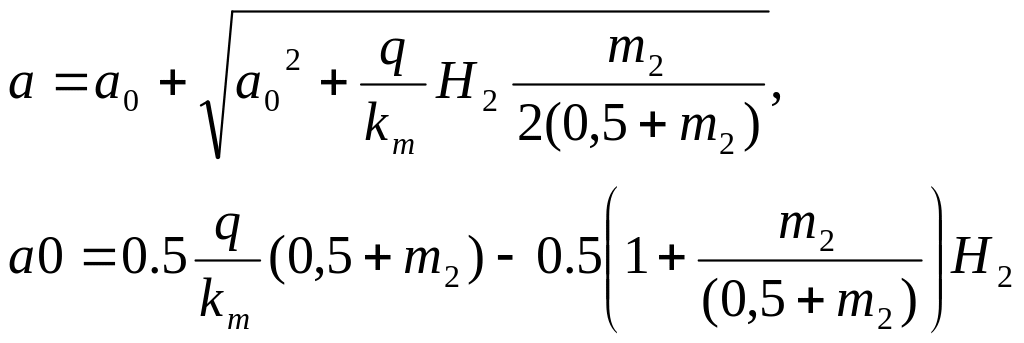
где

Ординаты кривой депрессии вычисляются по уравнению

Кривая депрессии исправляется визуально в зоне верхового откоса.

Однородные плотины на водонепроницаемом основании конечной мощности Т.

6. I Глотана без дренажа (к,„ = к_ос)

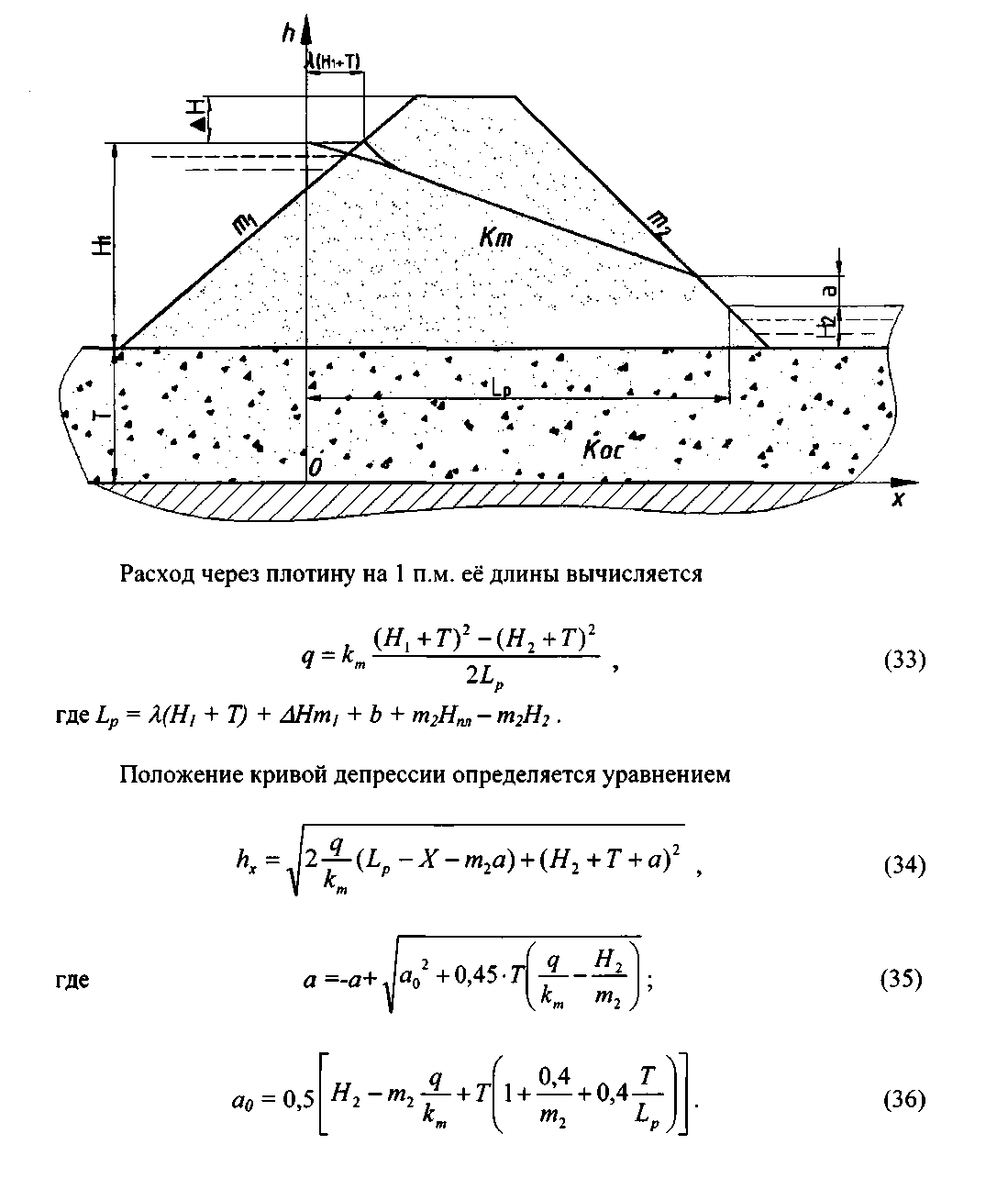
Расход через плотину на 1 п.м её длины вычисляется

7. Плотина с трубчатым дренажом (к_т = к_ос)

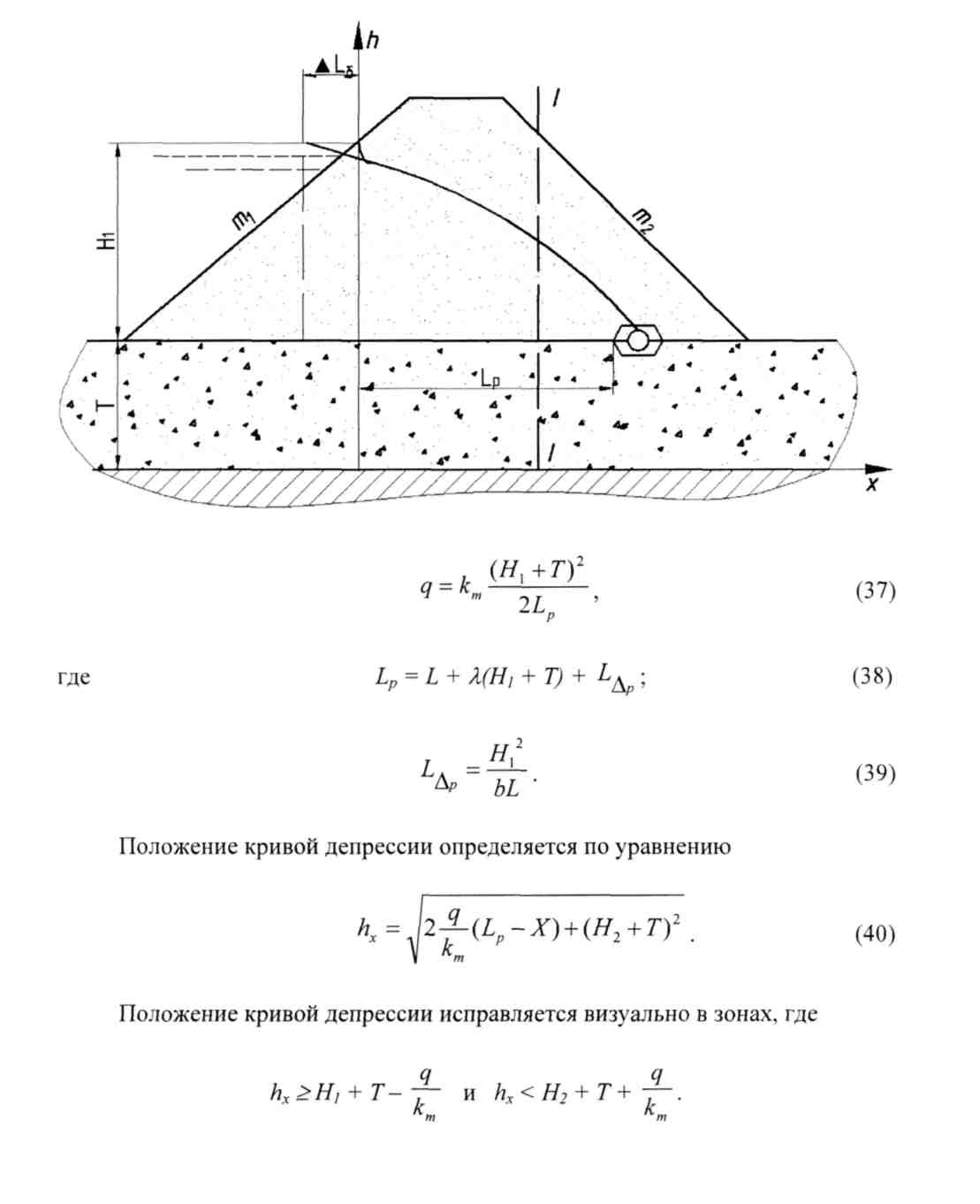
8. Плотина с дренажным банкетом

-75-

9. Плотина с трубчатым дренажом на водопроницаемом основании.

к < к

"-т ^ "-ос

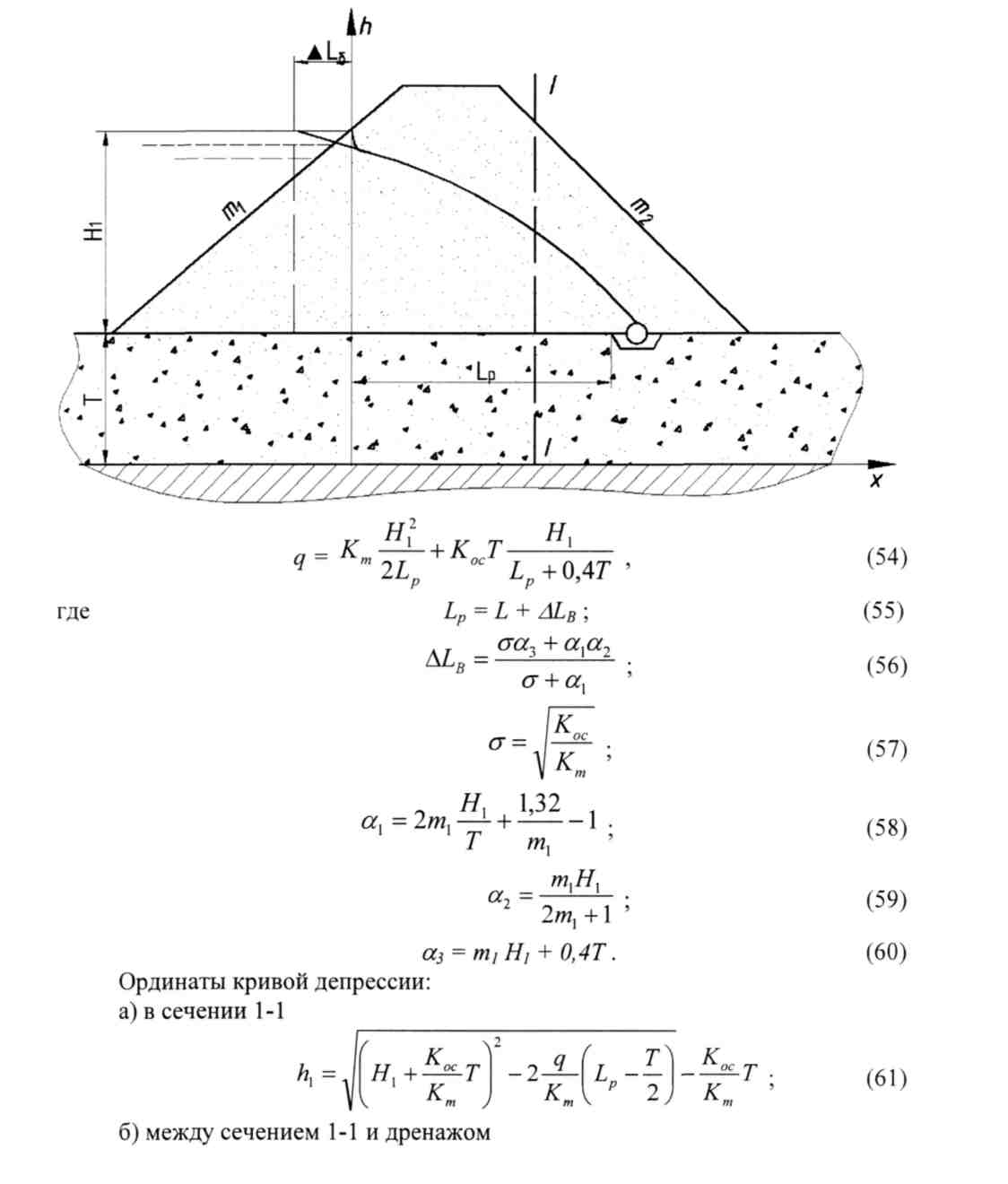
Кривая депрессии исправляется в зоне верхового откоса.

Плотины неоднородные на малопроницаемом основании

10. Плотина с ядром (к_т/ к_я < 100).

По способу виртуальных длин плотину приводят к однородной, причем

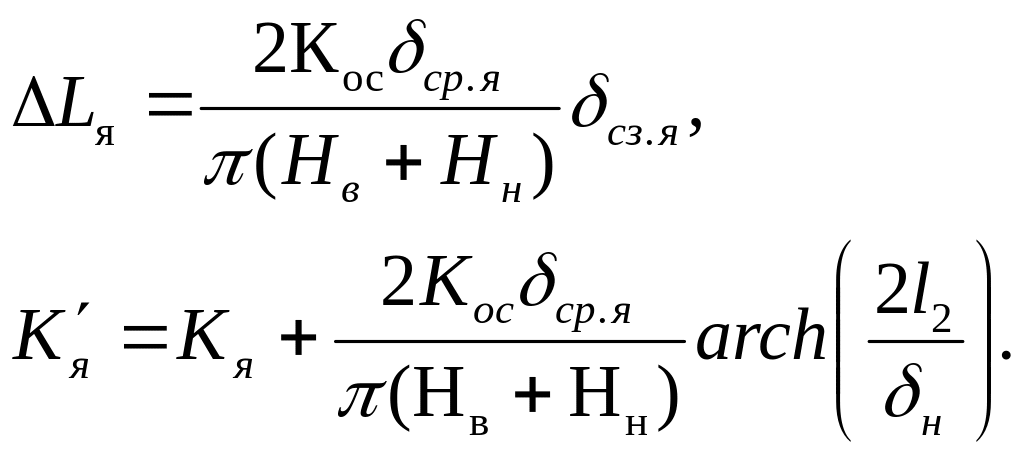
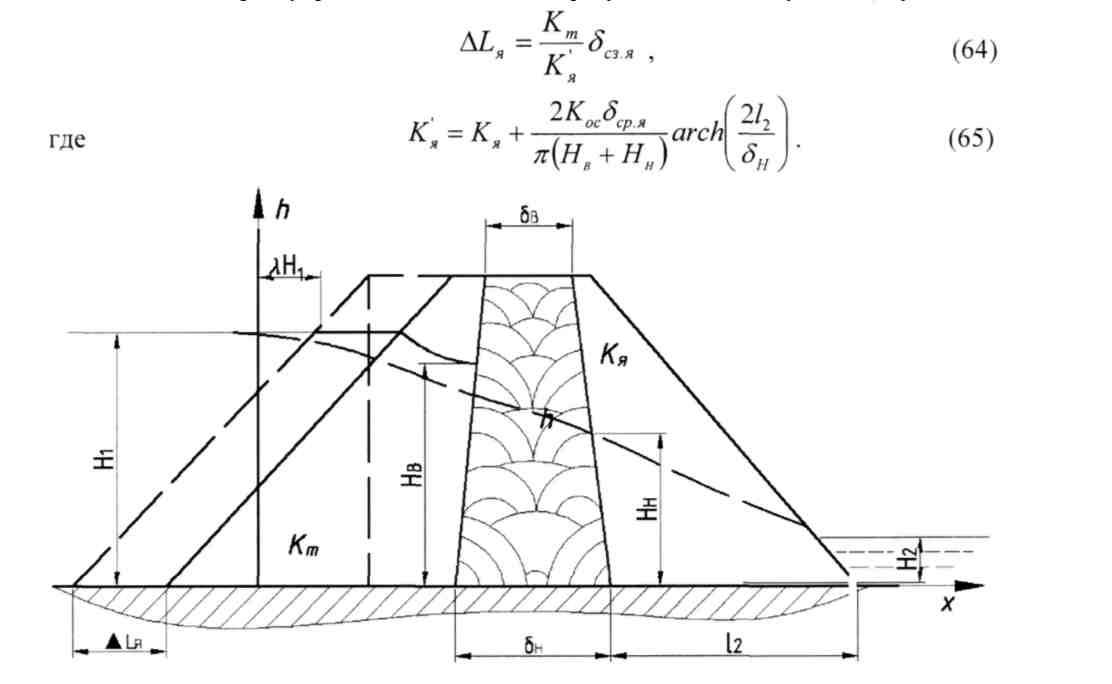
В первом приближении принимают Н_в - Я/, H_H = Н₂, затем их уточняют расчетом.

Величина обратная гиперболическая функция ко

синуса, определяется через логарифмическую функцию

Если к_я = к_ос, тогда

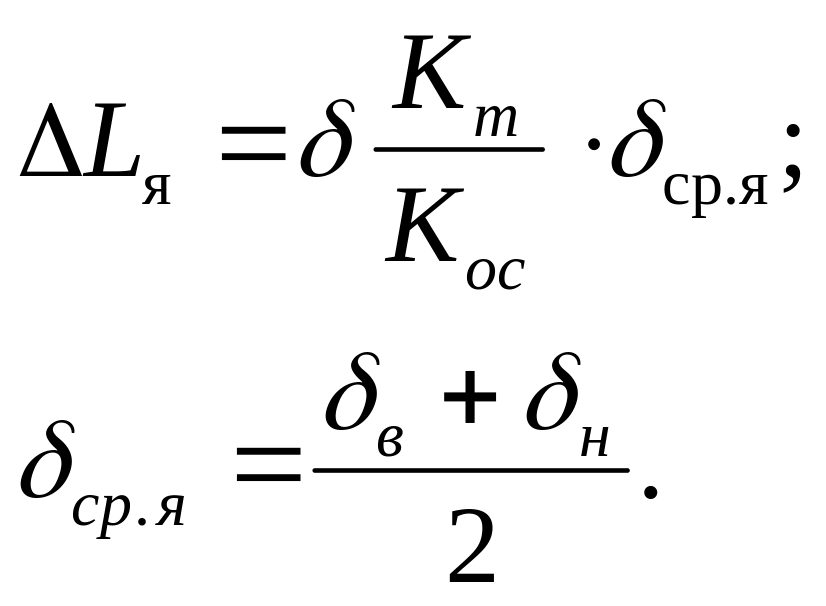
Величины q и h_x определяются после приведения плотины к однородной по формулам (17), (21), (33), (34).

11. Плотина с экраном.

По способу виртуальных длин плотину приводят к однородной, причем

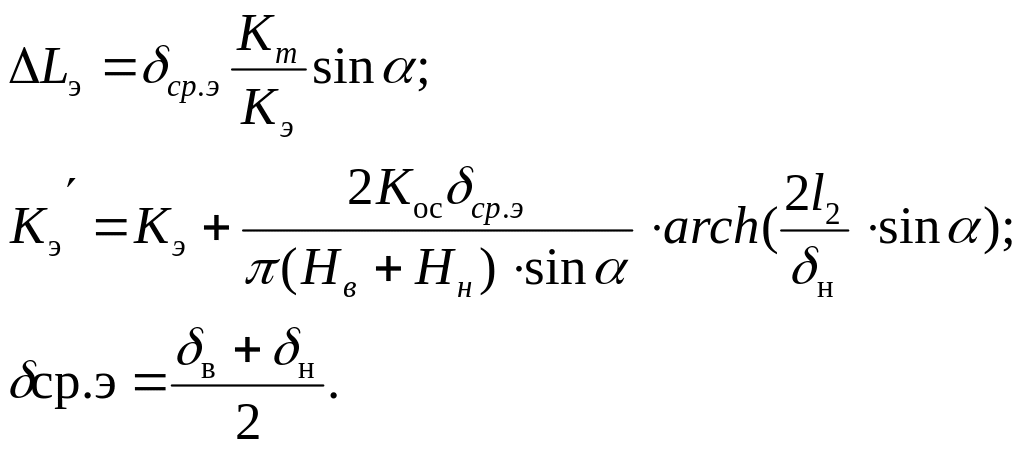
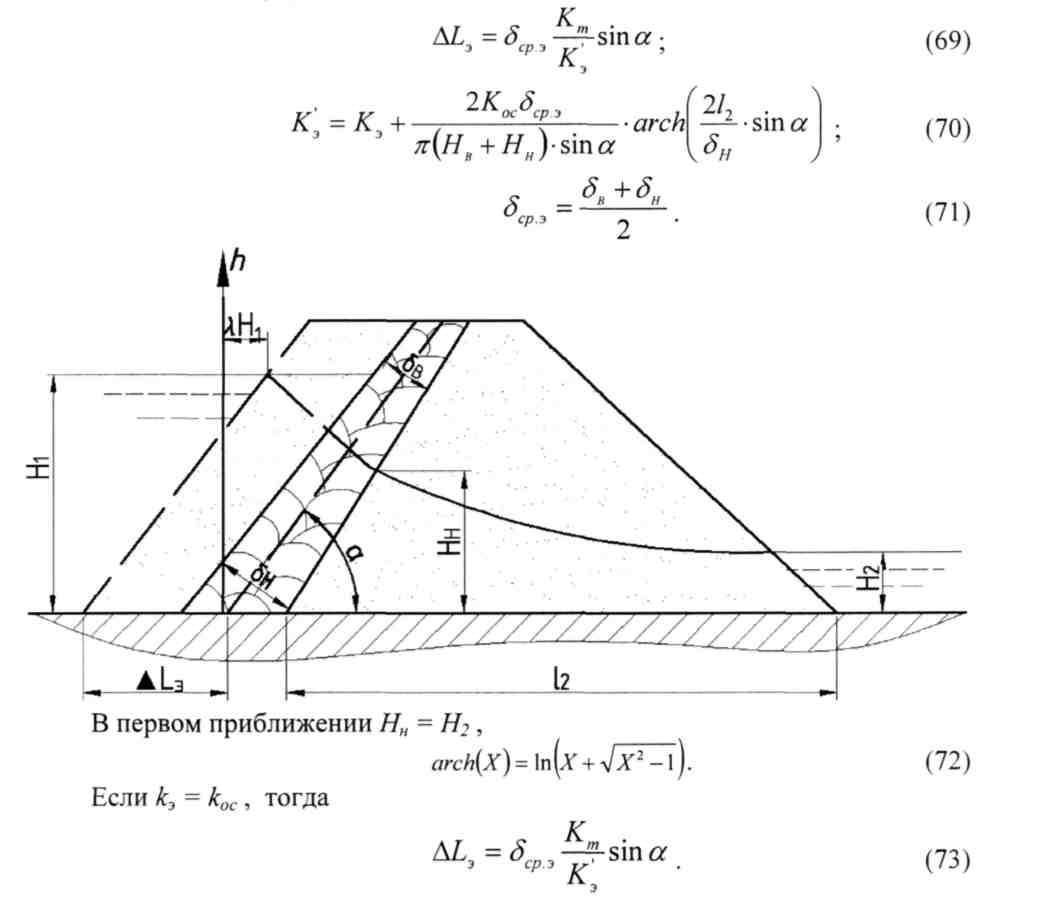
В первом приближении Н_н=Н₂

Если k_э=k_oc

, тогда

Расчет q и h_x производится по формулам (17), (21).

Плотины неоднородные на водонепроницаемом основании конечной мощности (к_ос = к_т).

12. Плотина с экраном, понуром, трубчатым дренажом или дренажным банкетом.

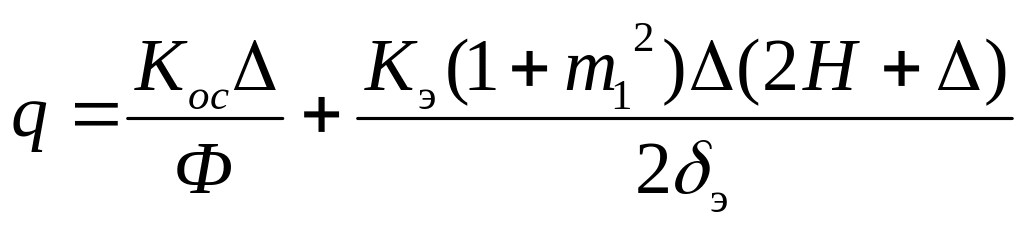
где

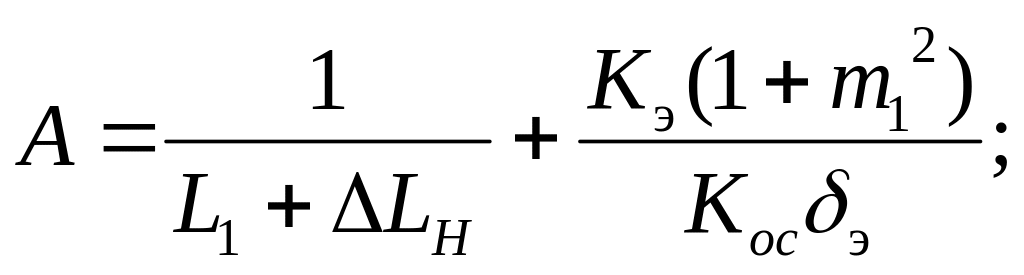
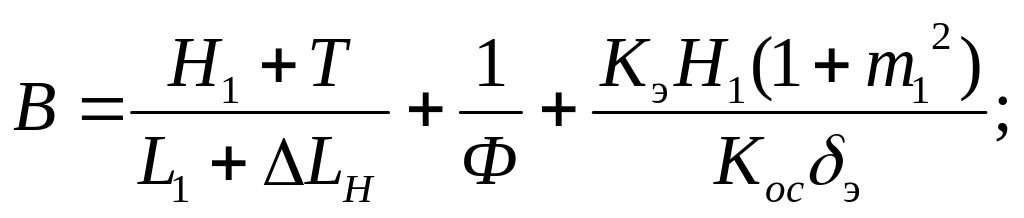
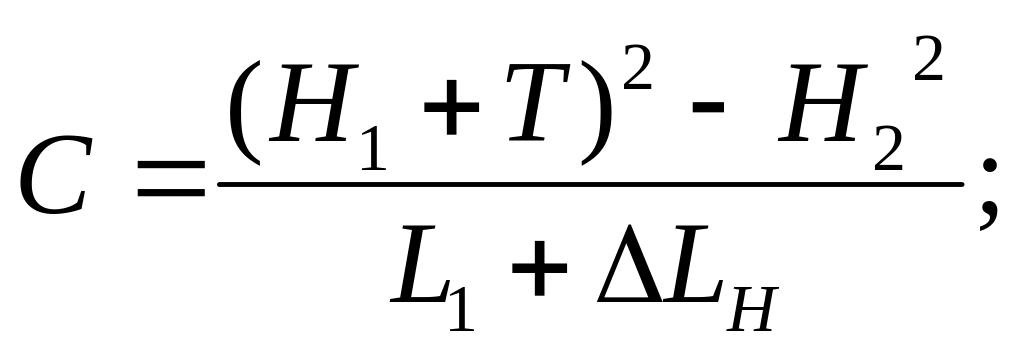
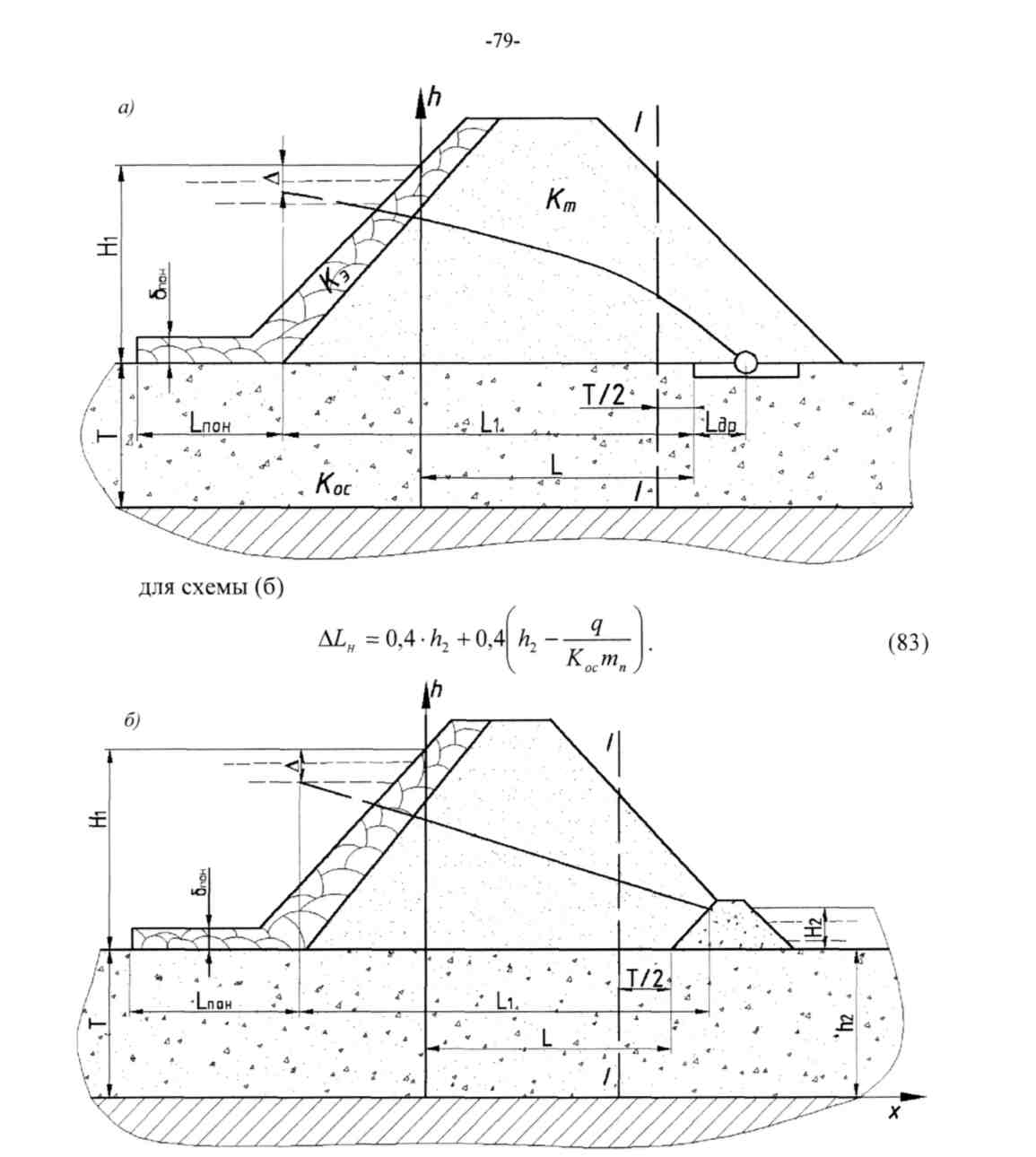
Для схемы (а)

th(X)- тангенс гиперболический

Ординаты кривой депрессии вычисляются по уравнениям :

а) с трубчатым дренажом - уравнения (61), (62), (63);

б) с дренажным банкетом - уравнения (51), (52), (53).

Для схемы (б)

(83)