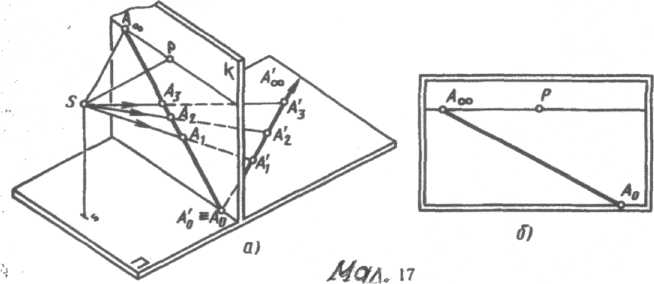
§ 5. Перспектива нескінченно продовженої прямої

Задамо в предметній площині апарата, що проектує, довільно спрямовану пряму і побудуємо її перспективу (мал. 16, а). Для цього скористаємося точкою — початком прямої, у якій вона перетинає основу картини. Перспектива цієї точки збіжиться із самою точкою (А_о = А'_о). Іншу точку А'₁ відзначимо (задамо) на прямої довільно і побудуємо її перспективу описаним вище способом (див. § 4). Відрізок А₀А₁ представить на картині перспективу деякої ділянки заданої прямої.

П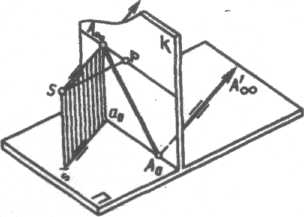 еремістимо уздовж заданої прямої точку А'₁ у положення... . Тоді на картині точка Аі буде переміщатися уздовж прямої , займаючи відповідно положення ... . Помітимо, що кути нахилу променів зору, спрямованих у точки до висоти точки зору збільшуються і спрямовують до 90°. Тому промінь зору, проведений у нескінченно вилучену точку А'_∞ прямої, яка задана, буде спрямований паралельно цієї прямої (sSA_∞=90°) і перетне її в невласній точці предметного простору. Точка А_ж (перетинання променя зору з картиною) є перспективою нескінченно вилученої точки заданої прямої А^А^. З побудови бачимо, що перспектива прямої А₀А_оа не може бути продовжена нескінченно, вона має межу й обмежена граничною точкою Д, цієї прямої (мал. 16, б).

Мал. 17

Перспективне зображення нескінченне вилученої точки прямої називається її граничною точкою (мал. 17).

Для побудови граничної точки нескінченно продовженої горизонтальної прямої проводять промінь зору паралельно заданої прямої і знаходять точку його перетинання з площиною картини. Для цього через промінь зору і висоту точки зору проводять допоміжну площину, що горизонтально-проектує. Потім будують лінію перетинання картинної і допоміжної площин, проводячи перпендикуляр до основи картини. Точка перетинання променя зору з перпендикуляром визначить граничну точку нескінченно продовженої прямої, яку шукали.

Помітимо, що в будь-якої прямої, що лежить у предметній площині ( ) або їй паралельної ( ), гранична точка знаходиться від основи картини на відстані, рівній висоті точки зору (мал. 18, а, б). Отже, промені зору лежать у променевій площини обрію, а граничні точки цих прямих знаходяться на лінії обрію.

О тже, перспектива нескінченно продовженої прямої що лежить у предметної площині або їй паралельної, обмежена граничною точкою, яка розташована на лінії обрію. (Закон граничної точки нескінченно продовженої прямої.)

Мал. 18

§ 6. Перспектива прямої загального положення

На апараті, що проектує, у предметному просторі прямі можуть бути розташовані по-різному щодо предметної і картинної площин, тобто займати загальне чи часне положення. Прямі загального положення розташовані під довільним кутом до предметної і картинної площин (див. мал. 15, а, б). Прямі часного положення розташовані паралельно або перпендикулярно до предметної і картинної площин (див. мал. 16, 17).

Пряма загального положення в залежності від напрямку може бути висхідної і спадної. Висхідної називається така пряма, яка, віддаляючись від глядача, спрямована знизу нагору. Спадної називається така пряма, яка, віддаляючись від глядача, спрямована зверху вниз.

Розглянемо побудову перспективи висхідної прямої. Задамо в предметному просторі апарата, що проектує, висхідну пряму і її проекцію А'а' на предметну площину (мал. 19,а). Спочатку будують перспективу Аа проекції висхідної прямої. Вона є довільно спрямованої прямої, що лежить у предметній площині. Її зображення на картині одержують побудовою точки А и граничної точки а . Для визначення граничної точки проекції даної прямої паралельно їй направляють промінь зору (S а || А'а' ) до перетинання з лінією обрію.

Для побудови граничної точки висхідної прямої спрямовують паралельно їй промінь зору (SА || А'А' ) і знаходять точку його перетинання з площиною картини. Променева площина SА а є площиною, що горизонтально-проектує, тому що за побудовою вона паралельна площині висхідної прямої. Вона перетинає картину по прямій А а , яка перпендикулярна лінії обрію. Тому промінь зору SА перетинає картину в точці А , яка розташована на перпендикулярі а А до лінії обрію.

Мал. 19

На картині, з'єднавши точку А с граничними точками прямої А і її проекції а , одержують перспективне зображення висхідної прямої загального положення (мал. 19, б).

О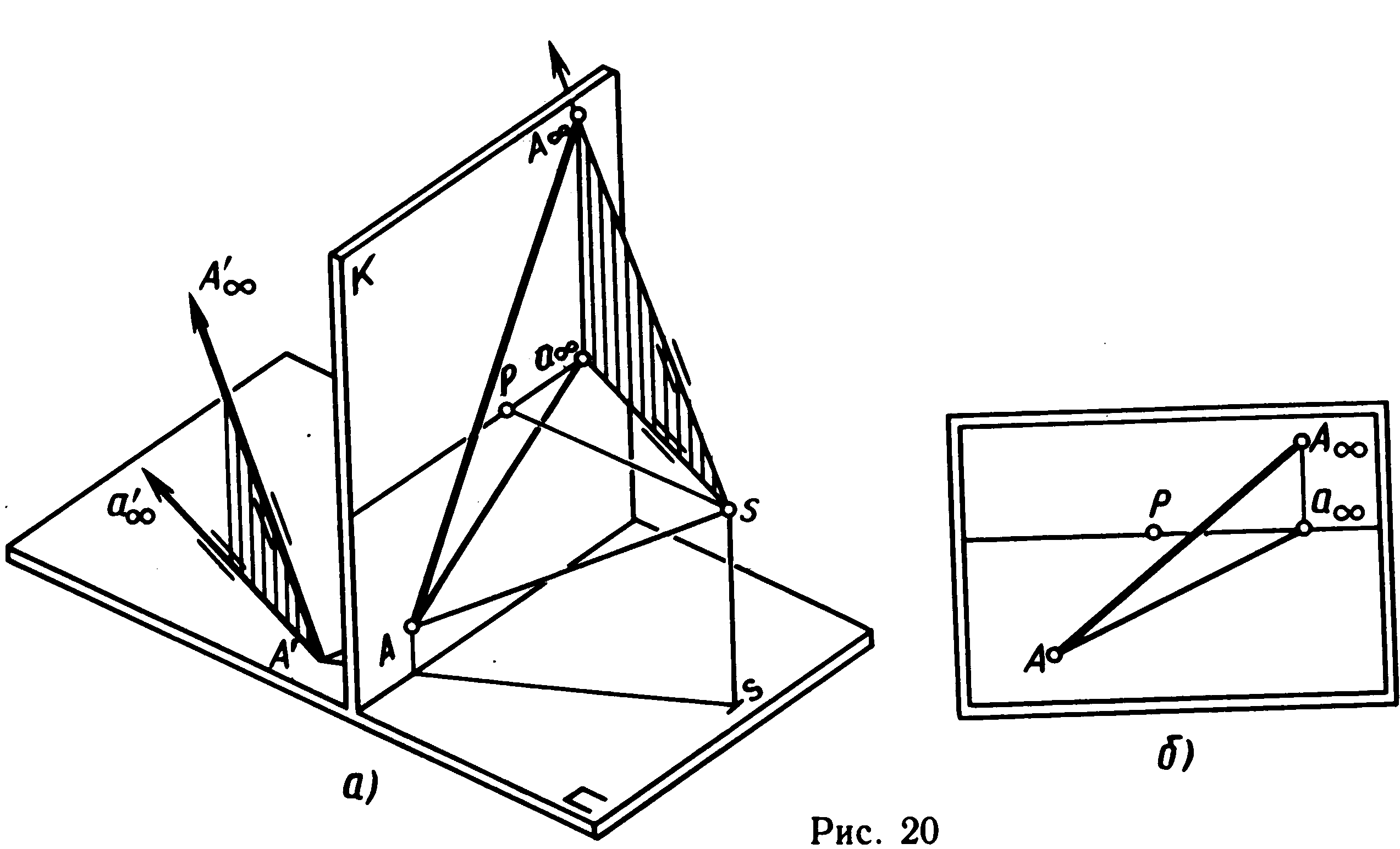 тже, висхідна пряма загального положення в перспективі обмежена граничною точкою, що знаходиться над лінією обрію і лежить на перпендикулярі, проведеному через граничну точку проекції цієї прямої. (Закон граничної точки висхідної прямої загального положення.)

Розглянемо побудову перспективи спадної прямої загального положення. Задамо в предметному просторі апарата, що проектує, спадну пряму і її проекцію А'а' на предметну площину (мал. 20, а).

Спочатку будують перспективу точки А і її проекцію а спадної прямої. Потім знаходять граничні точки А і а спадної прямої і її проекції. Для цього проводять промінь зору паралельно проекції заданої прямої (S а || а'а' ). У перетинанні променя зору з лінією обрію відзначають граничну точку а проекції спадної прямої.

Д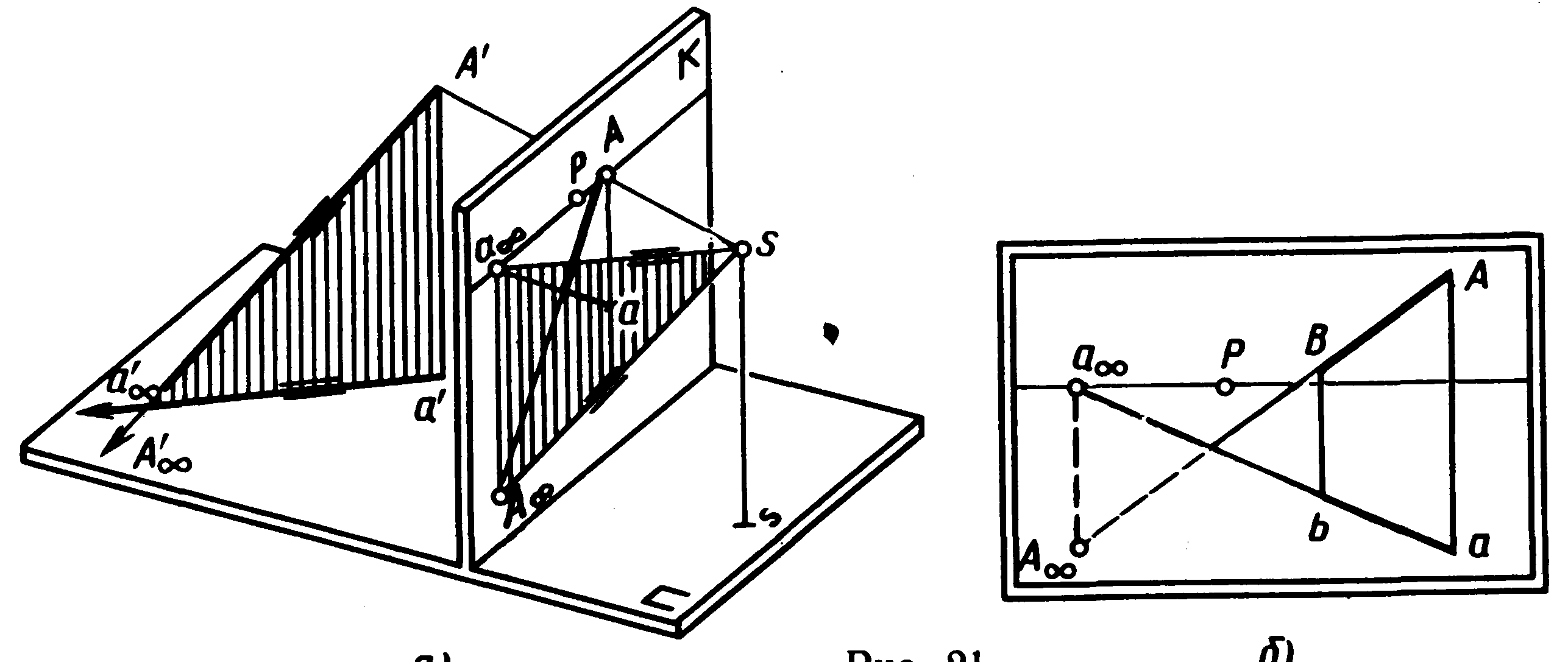 алі проводять промінь зору паралельно спадної прямої загального положення (SА || А'А' ) і будують точку його перетинання з картиною. Вона знаходиться на лінії перетинання променевої площини А S а з картиною.

Мал. 20

Променева площина горизонтально-проектує, тому що паралельна площині, яка утворена заданою спадною­ прямою і її проекцією на предметну площину. Тому променева площина перетне картину по прямій А а , яка перпендикулярна лінії обрію. Звідси промінь зору SА перетне картину в точці А , що лежить на перпендикулярі до лінії обрію.

На картині, з'єднавши точку А з А і точку а з а , одержують перспективне зображення спадної прямої загального положення (мал. 20, б).

Отже, спадна пряма загального положення в перспективі обмежена граничною точкою, що знаходиться під лінією обрію і на перпендикулярі, проведеному через граничну точку проекції цієї прямої. (Закон граничної точки спадної прямої загального положення).