Питання і вправи для самоконтролю

1. Що таке перспектива? Дайте визначення поняттю «перспектива».

2. Які види перспективи застосовують у даний час у практиці образотворчого мистецтва? У чому їхня сутність?

3. У чому полягає сутність методу центрального проектування?

4. Назвіть елементи апарата, що проектує.

5. Назвіть елементи картини. Як вони зв'язані з елементами апарата що проектує?

6. Як задають елементи картини при створенні композиції? Як визначають і задають елементи картини при малюванні з натури?

7. Що таке поле зору людини і як його визначають?

8. Що таке поле і кут ясного зору?

9. Визначите кут ясного зору, якщо діаметр поля ясного зору 40 мм, а дистанційна відстань 60 мм.

10. Визначите дистанційну відстань, якщо діаметр поля ясного зору 50 мм, а кут ясного зору складає 30°.

Глава 2. Зображення точки і прямої в перспективі

§ 4. Перспектива точКи і відрізка прямої

Усі предмети і явища навколишньої нас дійсності являють собою сукупність точок, прямих, площин. Точка є основним і найпростішим геометричним елементом простору. З неї починають вивчення і побудова перспективних зображень на картині.

У предметній площині апарата, що проектує, задамо точку (мал. 13, а). Потрібно побудувати її перспективу. Спочатку направляють у точку А' промінь зору SА' і знаходять точку перетинання його з картиною. Для цього через висоту точки зору Ss і промінь, що проектує, SА' проводять допоміжну площину, з'єднавши точку стояння S із проекцією точки а' (А' ≡ а'). Потім будують лінію перетинання допоміжної площини з картиною. Для цього відзначають точку а_о перетинання основ картини і допоміжної площини. Допоміжна площина - горизонтально-проектує, тому що вона проходить через перпендикуляр Ss і картина перпендикулярна до предметної площини. Отже, лінія їхнього перетинання буде також перпендикулярна до предметної площини і до основи картини. Тому через точку а_о проводять пряму, перпендикулярну до основи картини. Цей перпендикуляр перетне промінь зору SА' у точці а, що і буде шуканим перспективним зображенням точки А', заданої в предметній площині. На картині (мал. 13, б) положення точки А' ≡ а' визначають відстанню р_оа_о вправо від лінії головного вертикаллю і перпендикуляром а_оА до основи картини.

На цьому ж апараті, що проектує, задана точка В' (див. мал. 13, а). Її просторове положення визначається перпендикуляром В'b' до предметної площини, тобто проекція b' є підставою точки В'. Спочатку будують перспективу заданої точки. Для цього проводять промені зору в точку В' і її проекцію b' і знаходять точки перетинань їх з картиною. Уклавши промені зору і висоту точки зору в площину, що горизонтально-проектує, з'єднують точку стояння s із проекцією точки b'. Після цього будують лінію перетинання допоміжної і картинної площин і відзначають точку b_о перетинання їх основ. Через отриману точку b_о проводять у площині картини перпендикуляр до її основи. Точки перетинання променів зору з перпендикуляром (лінією перетинання площин) визначать перспективу точки В и її основи b. Відрізок Вb є перспективою відстані, на якому точка В' знаходиться від предметної площини.

На картині (див. мал. 13, б) просторове положення точки В визначають відстанню р_оb_о уліво від лінії головного вертикаля і перпендикуляром В до основи картини.

Зіставимо положення двох заданих точок у предметному просторі з перспективним зображенням їх на картині. На апараті, що проектує, точка А' розташована ближче до глядача, чим точка В'. На картині це відбито відстанню вторинних проекцій а і b точок А і В до основи картини а_о і b_о (аа_о< bb_о).

Для побудови перспективи точки направляють промені зору в дану точку і її проекцію на предметній площині і знаходять точки перетинання їх з картиною. Для цього через висоту точки зору і промені, що проектують, проводять допоміжну площину, що горизонтально-проектує, і будують лінію перетинання її з картиною. Точки перетинання променів зору з лінією перетинання площин визначать перспективу заданої точки і її проекції.

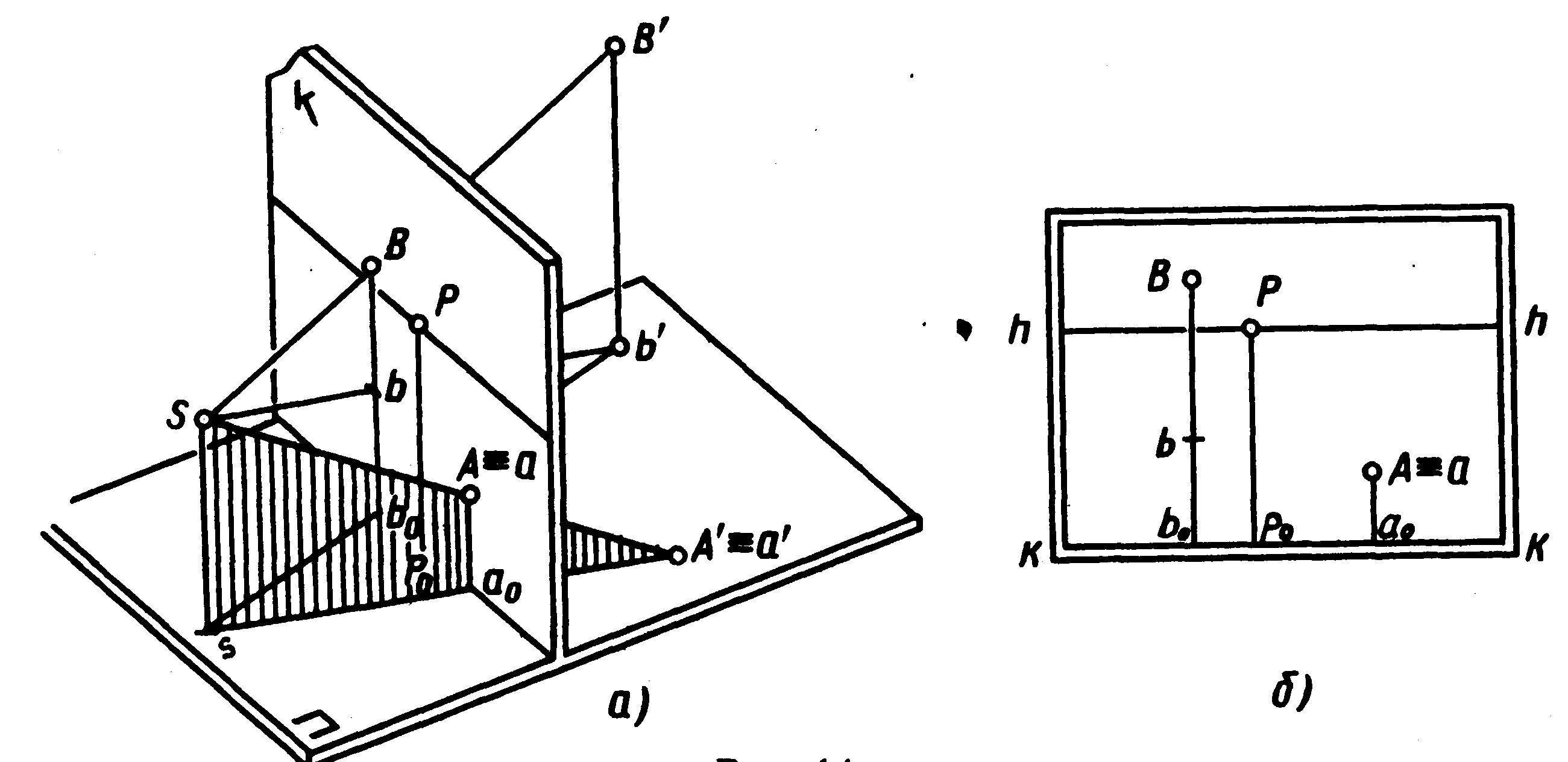
Мал. 13

Помітимо, що точка А' лежить у предметній площині. Її відстань від предметної площини дорівнює 0, тому проекція точки а' на предметну площину збігається із самою точкою А' (А' ≡ а'). Точка В' знаходиться в предметному просторі на відстані В'b' від предметної площини.

П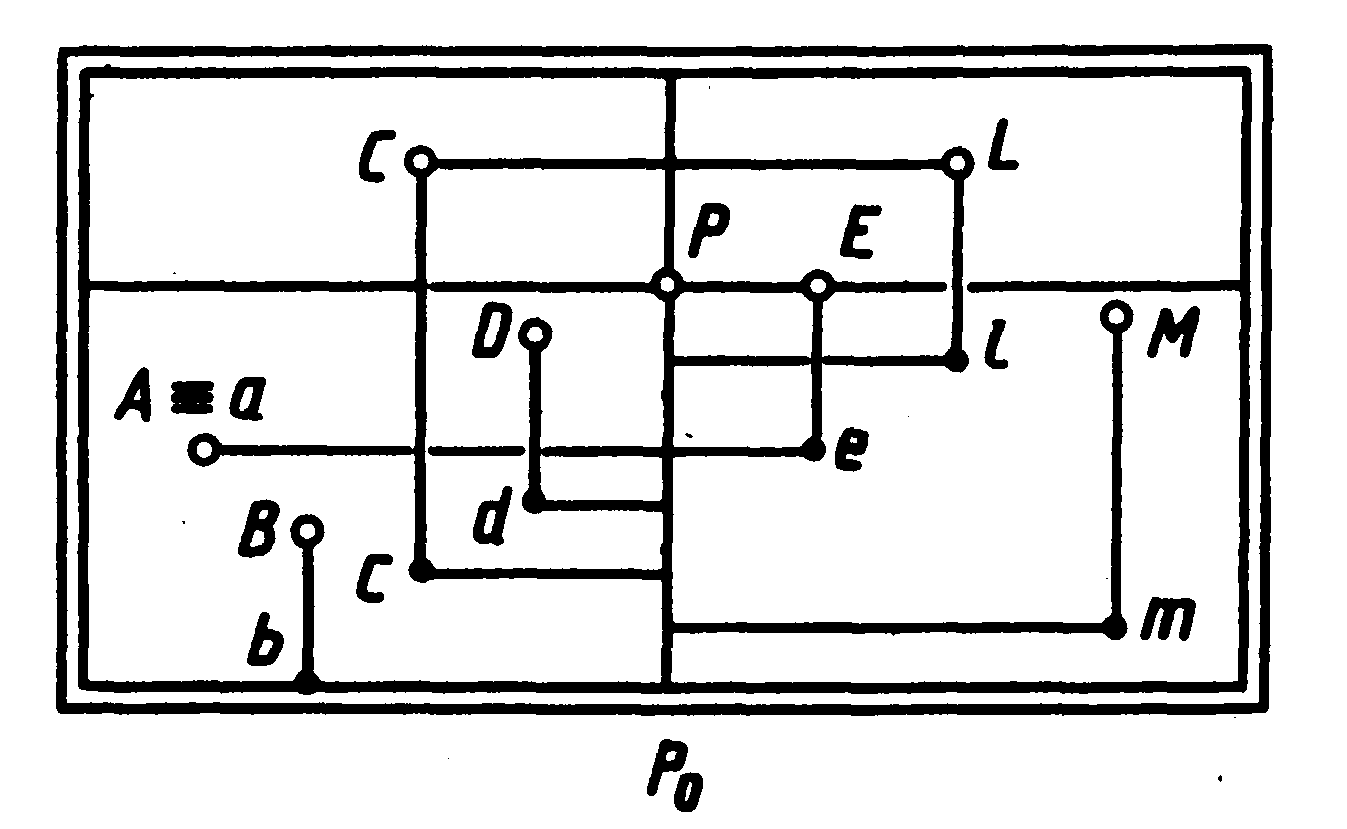 оложення точки називається часткою, якщо вона лежить у предметній чи картинній площині. Положення точки називається загальним, якщо вона розташована в предметному просторі і знаходиться на деякій відстані від предметної і картинної площин.

На підставі вищевикладеного правила по зображенню на картині можна визначити просторове положення точки. Так, на картині (мал. 14) задано сім точок (A, B, C, D, E, L, M). Потрібно визначити їхнє взаємне положення.

Мал.14

Помітимо, що чотири точки (A, B, C, D) розташовані в лівої частині картини (вони знаходяться ліворуч від лінії головного вертикала), а три

точки (Е, L, М) -у правій частині.

Щодо предметної і картинної площин точки А і В займають часткове положення, тому що точка А лежить в предметній площині, а точка В — у картинній. Інші п'ять точок займають загальне положення.

Щодо лінії обрію точки А, В, D, М знаходяться нижче її, точка Е — на рівні лінії обрію, точки С і L — вище обрію. Оскільки точка А лежить у предметній площині, то вона нижче усіх. Вище всіх точка L, хоча вона на картині знаходиться на одному рівні з точкою С, але перспектива l її основи більш віддалена, чим с.

Для визначення далекості точок від картини варто порівняти відстань від основи картини до вторинних проекцій точок на предметну площину, тобто їхніх основ. Точка В найблизька , тому що вона лежить у площині картини. За нею послідовно віддалені точки М, С, D. Точки А і Е віддалені на однакову відстань від картини, тому що їхні основи знаходяться на одній горизонтальній лінії. Далі усіх від картини знаходиться точка L.

П ерспектива відрізка прямої. На апараті, що проектує, перспективу прямої можна визначити як сукупність точок перетину з картинною площиною променів зору, проведених до кожної точки даної прямої. Ці промені зору утворять променеву площину. З геометрії відомо, що перетинання двох площин (у даному випадку променевої і картини) здійснюється по прямій лінії (мал. 15, а). З цього випливає, що перспектива прямої є пряма лінія. В окремому випадку, коли пряма збігається з направленням променя, що проектує, її перспективним зображенням буде точка.

Для зображення на картині відрізка прямої будують перспективу двох його точок. Пряма, що з'єднує знайдені точки, на картині визначить перспективу заданого відрізка.

Мал. 15

Розглянемо на апараті, що проектує, побудова в перспективі заданого в просторі прямолінійного відрізка Спочатку будують перспективу А і В двох точок. З'єднавши на картині точки А і В, а також їхні проекції а і b, одержують перспективне зображення заданого відрізка АВ. Відстань від точок до їхніх проекцій аа і Вb визначить на картині зображення перпендикулярів, що зв'язують заданий відрізок із предметною площиною (мал. 15, б).