§17. Побудова в перспективі кутів, довільно розташованих у горизонтальній площині

Положення будь-якого кута (особливо прямого), який лежить в предметній чи в паралельній їй площині має широке застосування при побудові навколишніх нас предметів і взаємного їхнього розташування.

Д ля побудови перспективи кута, що лежить у горизонтальній площині, задають його натуральну величину при сполученій точці зору і продовжують сторони до перетинання з лінією обрію. Отримані точки перетинання будуть граничними точками сторін шуканого кута, вершина якого може бути задана в будь-якім місці. На основі цього правила будують заданий кут на картині (мал. 69) Для цього при сполученій точці зору задають натуральну величину кута і продовжують його сторони до перетинання з лінією обрію. Отримані точки і є

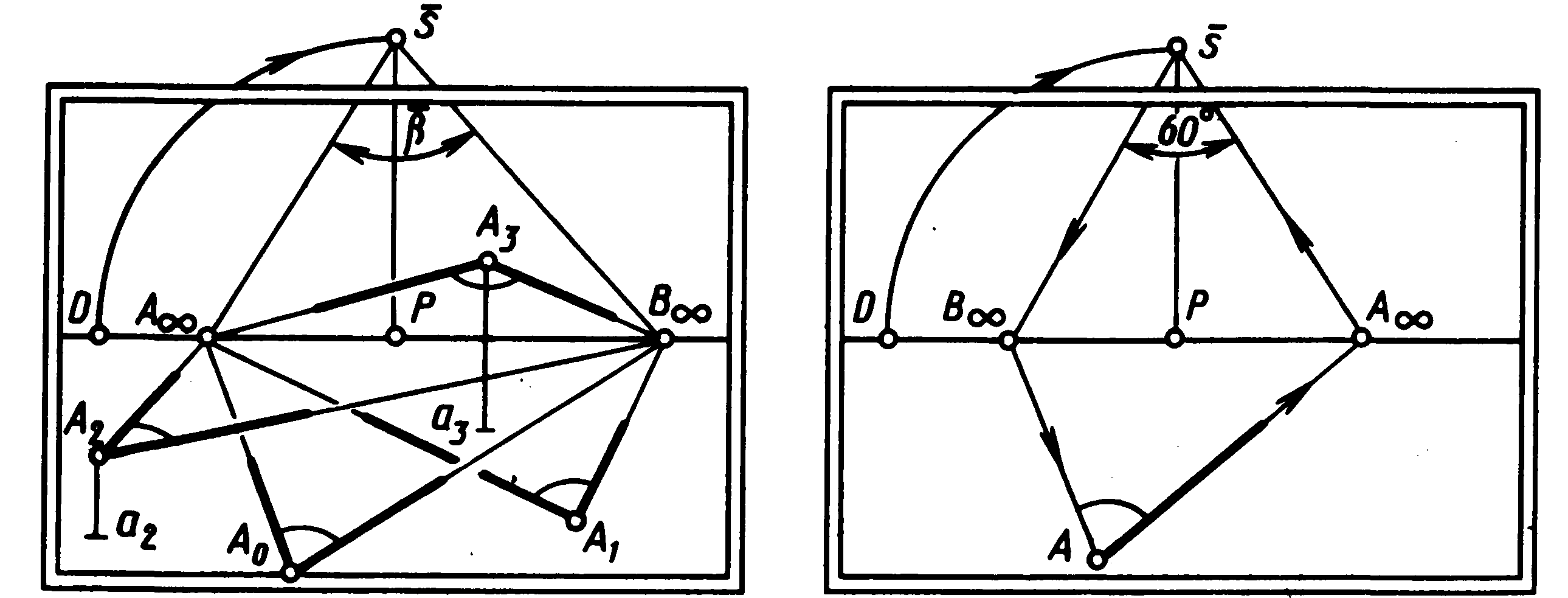
Мал. 69 граничними точками сторін заданого кута з вершиною А_о в перспективі.

Помітимо, що всякий кут на картині (мал. 70) з довільно обраною вершиною А_о , А₁ , А₂ , А₃ , ... і сторонами, що мають ті самі граничні точки і , дорівнює по величині куту , заданому при сполученій точці зору. Рівність кутів на картині визначається паралельністю сторін, що мають у перспективі загальні граничні точки, тобто точки сходу і . По зображенню на картині видно, що кути при вершині А_о й А₁ лежать у предметній площині, А₂ і Аз — у площинах, паралельних їй, при цьому кут А₂ — нижче лінії обрію, а кут Аз — вище.

На картині (мал. 71) у предметній площині задана вершина А і напрямок однієї зі сторін кута. Потрібно побудувати перспективу кута, що лежить у предметній площині і рівного в натурі 60°.

Побудову виконують у такій послідовності.

Спочатку визначають положення сполученої точки зору. Для цього з головної точки картини Р проводять перпендикуляр до лінії обрію і відкладають на ньому дистанційну відстань Р =РD.

Потім відзначають граничну точку заданої сторони кута. Для цього продовжують задану сторону кута до перетинання з лінією обрію.

Далі будують натуральну величину кута 60° при сполученій точці зору і заданій стороні . Для цього з'єднують граничну точку зі сполученою точкою зору . Відкладають натуральний кут 60° з вершиною і стороною . Потім продовжують другу сторону кута до перетинання з лінією обрію і визначають її граничну точку .

Мал. 70 Мал. 71

З’єднуючи задану вершину а з отриманою граничною точкою проводять другу сторону кута а . Кут а є перспективою заданого кута 60°.

Для визначення натуральної величини кута, що лежить у горизонтальній площині, по його зображенню на картині будують граничні точки сторін кута, продовживши їх до перетинання з лінією обрію. Отримані граничні крапки з'єднують із сполученою точкою зору. Кут при сполученій точці зору буде натуральною величиною кута, заданого на картині.

§ 18. Побудова окружності у перспективі

Загальні поняття. Уміння будувати в перспективі окружність потрібно не тільки для зображення на картині круглих предметів, але і для показу різних положень між окремими елементами предметів, наприклад напіввідчиненого вікна або двері, нахиленої картини або дзеркала, обрису тіней від круглих предметів і ін.

У перспективі зображення окружності може мати різний обрис. Це залежить від того, як розташована площина окружності щодо картини і точки зору.

В окремому випадку перспективою окружності буде окружність, якщо вона розташована в площині, паралельній картині, і її геометричний центр збігається з точкою Р. Іншій окремий випадок перспективи окружності — прямолінійний відрізок. Таке зображення виходить тоді, коли всі промені зору, спрямовані до точок зображуваної окружності, розташовані в одній променевій площині (наприклад, окружність у площині обрію або у площині головного променя зору). У всіх інших положеннях окружність на картині зобразиться лекальною кривою.

Побудова перспективи окружності на апарат, що проектує, полягає у визначенні точок перетинання променів зору, які проведені до точок заданої окружності, з картинною площиною. Сукупність цих променів зору утворить поверхню променевого конусу. Звідси перспектива окружності являє собою лінію перетинання поверхні променевого конуса з площиною картини.

У практиці побудови перспективи окружності найбільш часто зустрічається еліпс. З геометрії відомо, що це замкнена плоска крива, яка симетрична відносно двох взаємно перпендикулярних вісей (мал. 72, а). Велике та мала вісі еліпса перетинаються у центрі та розподіляються навпіл. Помітимо, що еліпси – зображення окружності у перспективі – втрачають ці властивості (мал. 72, б).

Щоб побудувати зображення окружності у перспективі знаходять окремі точки, яки належать кривій, та плавно з’єднують їх від руки. Плавність обрису ліній досягається досить великим числом точок, які розташовані близько одна до одній.

Т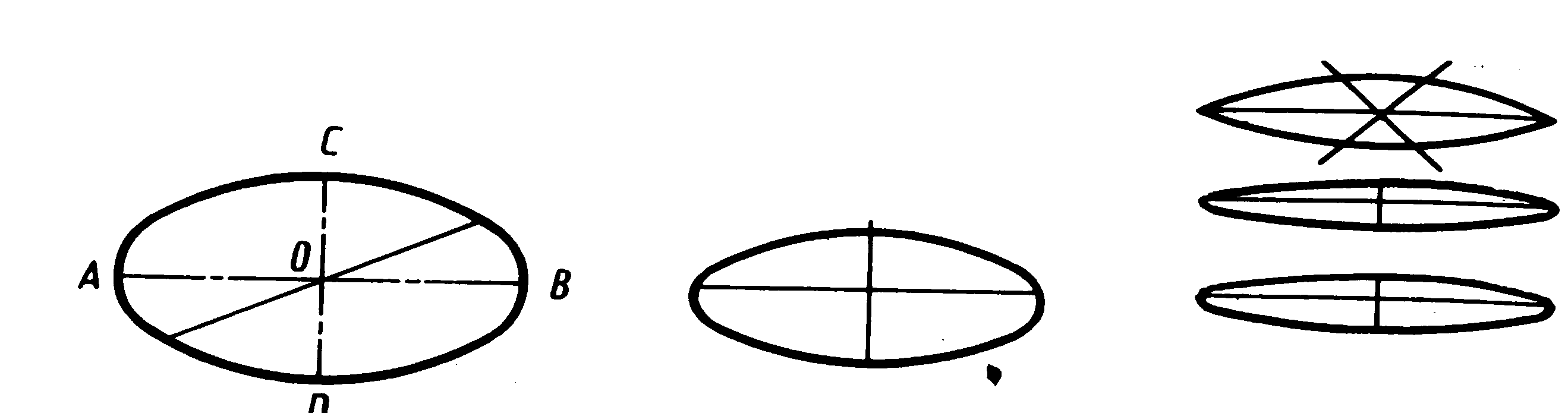 реба пам’ятати, що яким би вузьким не був еліпс, він не буде мати гострих кутів і малюватися з чітко баченими закругленнями (мал. 72, в).

а) б) в)

Мал. 72