§ 16. Побудова геометричних фігур у найпростішому положенні

Використовуючи матеріал, викладений у попередніх параграфах, можна побудувати перспективні зображення плоских кутів 90° і 45°, розташованих у горизонтальній і вертикальної площинах. А на основі позиційних і метричних властивостей— квадрат і прямокутник із заданою стороною, розташовані горизонтально і вертикально. Помітимо, що в даних прикладах визначення розмірів зображуваних фігур не передбачається.

Приклад 1. На картині (мал. 63) паралельно її основі задана сторона АВ квадрата. Потрібно побудувати квадрат, розташований у предметній площині. Спочатку при вершинах А і В прямі кути, для чого проводять глибинні прямі АР і ВР. Через вершину В (або А) - діагональ, граничною точкою якої є дистанційна. Точка С на прямій АР визначить положення сторони СЕ шуканого квадрата.

Приклад 2. На картині (мал. 64) задана сторона АВ квадрата вертикально. Потрібно побудувати квадрат, розташований перпендикулярно картинній і предметній площинам. Напрямком сторін прямого кута при вершинах А і В будуть глибинні прямі АР і ВР. Щоб відкласти на них сторони квадрата, приводять АВ у горизонтальне положення АВ₁ і переносять його величину за допомогою дистанційної точки на глибинну пряму АР. Точка С визначить кінець сторони СЕ квадрата.

П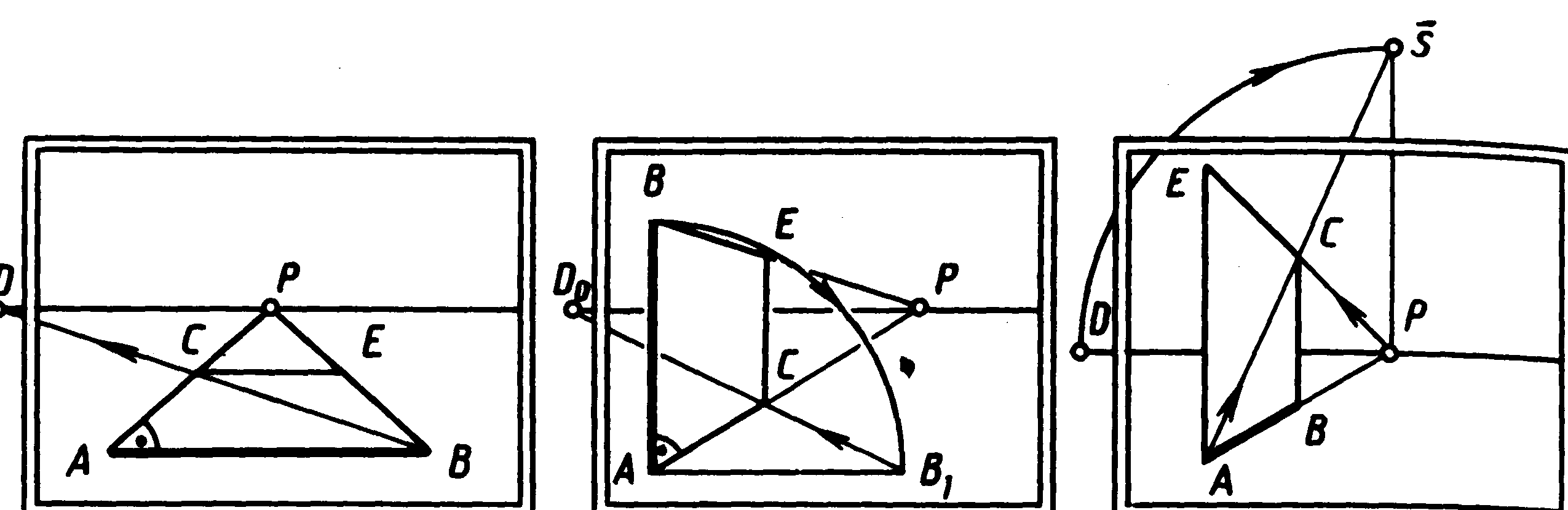 риклад 3. На картині (мал. 65) сторона квадрата АВ лежить на глибинної прямої. Потрібно побудувати квадрат, розташований перпендикулярно картинній і предметній площинам.

Мал. 63 Мал. 64 Мал. 65

Спочатку проводять через кінці А і В вертикальні прямі, що утворять із заданою стороною квадрата прямі кути. Потім через точку А проводять діагональ квадрата, граничною точкою якої буде сполучена точка зору . Через точки Р і С проводять верхню сторону СЕ квадрата, паралельну стороні АВ.

Приклад 4. На картині (мал. 66) сторона АВ квадрата вертикальна. Потрібно побудувати квадрат, розташований перпендикулярно до предметної площини і під довільним кутом до картини.

Сторони квадрата, перпендикулярні до АВ, лежать на прямих, граничною точкою яких може бути кожна на лінії обрію, наприклад . Величину сторони АС квадрата визначають за допомогою масштабної точки . Потім через точку С проводять вертикальну сторону СЕ шуканого квадрата.

П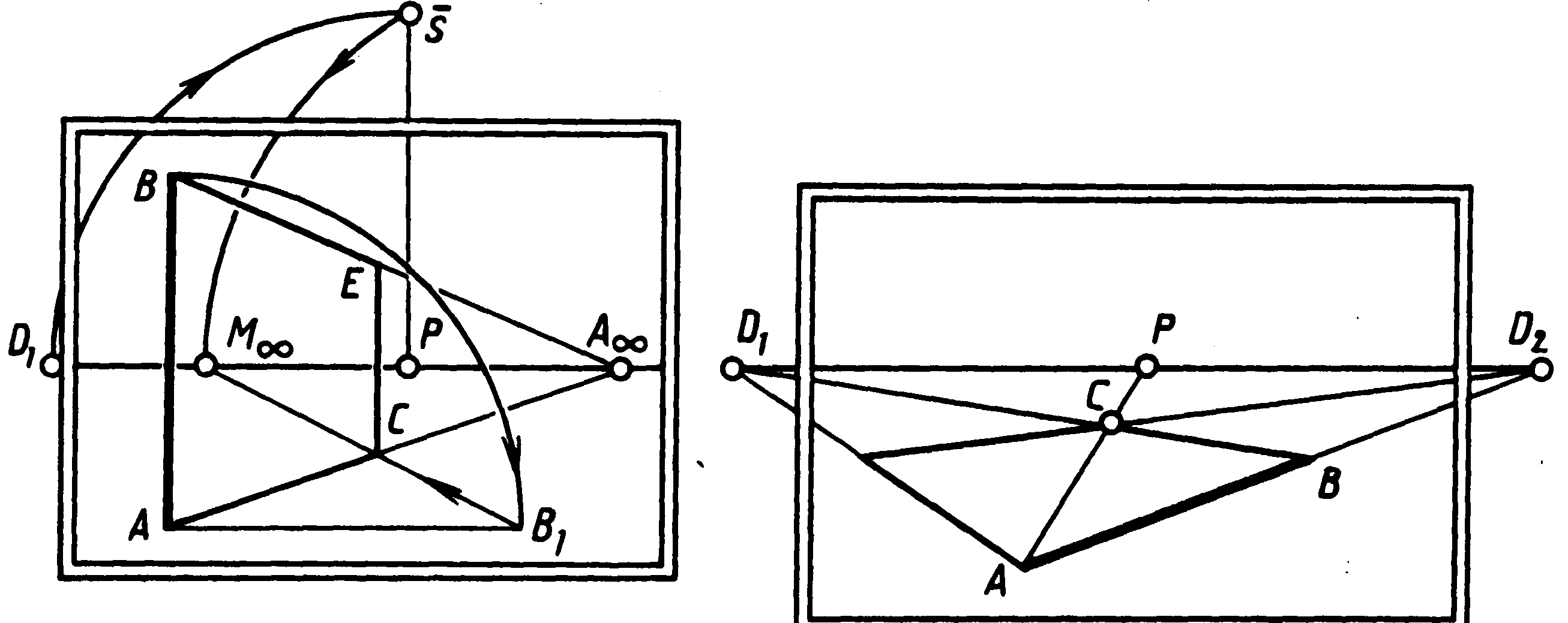 риклад 5. На картині (мал. 67) сторона АВ квадрата лежить у предметній площині. Її граничною точкою є дистанційна точка D₂. Потрібно побудувати квадрат, що лежить у предметній площині. Сторони прямих кутів при вершинах А і В лежать на прямих із точкою сходу D₁. Щоб визначити положення четвертої сторони квадрата, знаходять вершину С. Помітимо, що вона лежить на діагоналі квадрата з граничною точкою Р.

Мал. 66 Мал. 67

Приклад 6. На основі картини (мал. 68) задані сторони 0 – 1_о , 1_о – 2_о , 2_о – 3_о , 3_о – 4_о квадратних плит. Потрібно побудувати перспективне зображення частини підлоги, який викладений цими плитами.

С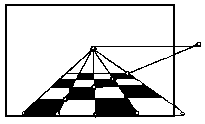 початку будують глибинні прямі сторін квадрата з головною точкою сходу Р. Потім через точки 0 і D проводять діагональ квадратів, яка у перетині з кожною глибинною прямою відмітить точки 1, 2, 3, 4. Через відмічені точки проводять горизонтальні прямі, паралельні основі картини. Вони визначать перспективу квадратних плит, які розташовані у площині підлоги.

Мал. 68