1.4 Рекурсивный фильтр Гаусса
Существует также ещё один метод фильтрации, основанный на аппроксимации преобразования Фурье гауссового ядра, который широко изложен в [1]. Покажем основную идею данного метода. Для этого представим экспоненту в виде ряда Тэйлора, тогда ядро запишется в виде:
,
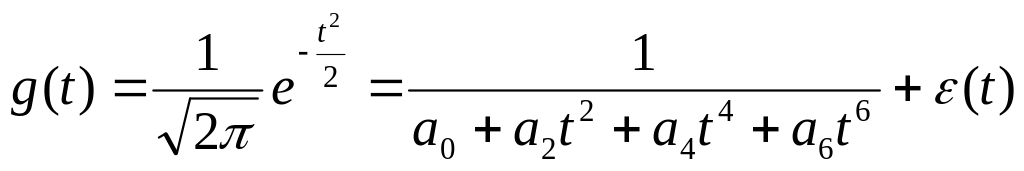где
= 2.490895,
=
1.466003,
=
-0.024393,
=
0.178257.
Далее мы будем аппроксимировать не само гауссово ядро, а его преобразование Фурье, которое хорошо известно:
.
Тогда, подставляя вместо σ2 - q, мы получим выражение вида:
.
И при s = jw:
.
Тогда выражение (выше),
может быть разложено на множители
=
*
:
.
И
.
После этого для представления G (s) в H(z), моно было бы воспользоваться стандартным билинейным преобразованием:
.
Но это бы привело к тому что в передаточной
функции появились бы нули, которых нам
лучше избежать. Поэтому мы применим
технику, описанную в [6] и
представим
для
и
для
.
Принимая T = 1, получим:
,
и
.
Оба выражения могут быть переписаны
как стандартные полиномы степени z
и
:
,
,
где
.
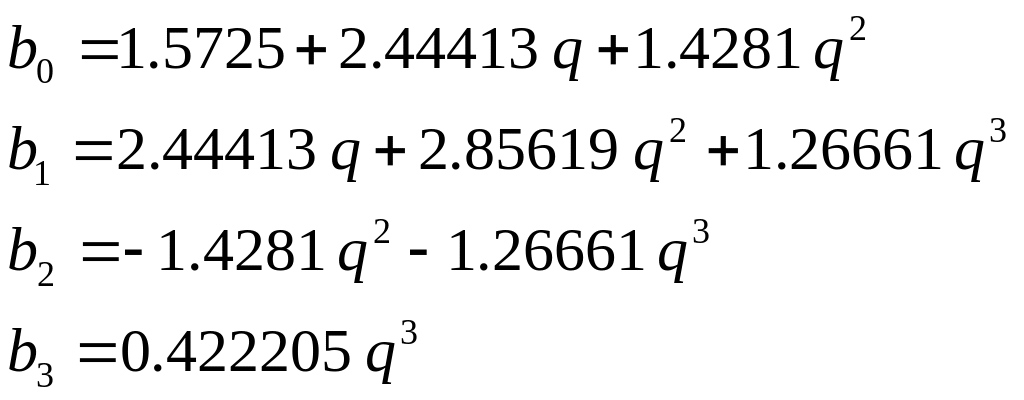Тогда реализация [1] советует следующую
фильтрующую стратегию. Входные данные
сначала фильтруются в прямом направлении
согласно выражению для
.
Тогда результат этой фильтрации, назовём
его w[n],
фильтруется в обратном направлении
согласно выражению для
,
и разностные выражения принимают
следующий вид:
Прямое:
,
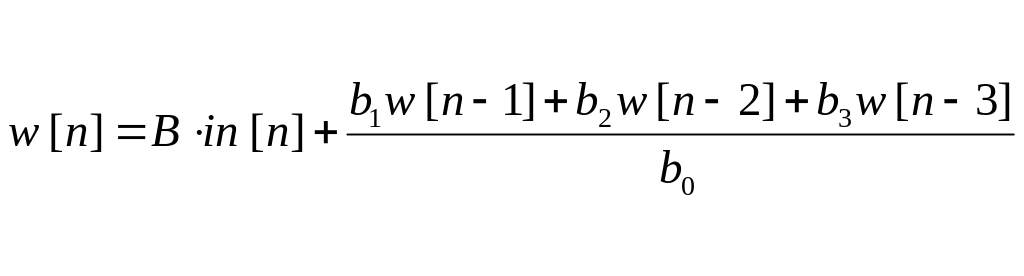обратное:
.
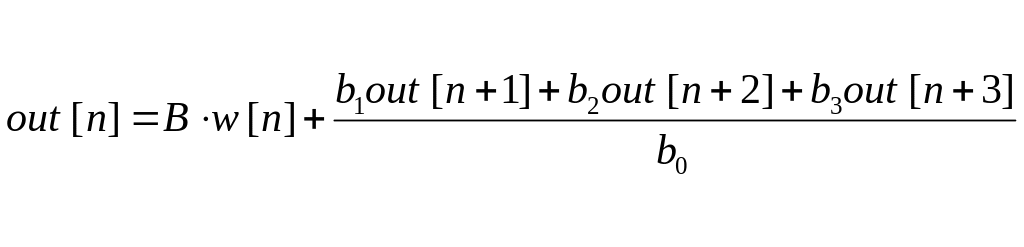Оба выражения используют нормализационную константу, которая имеет вид:
.
Стандартные рекомендации по выбору константы q представляют собой:
.
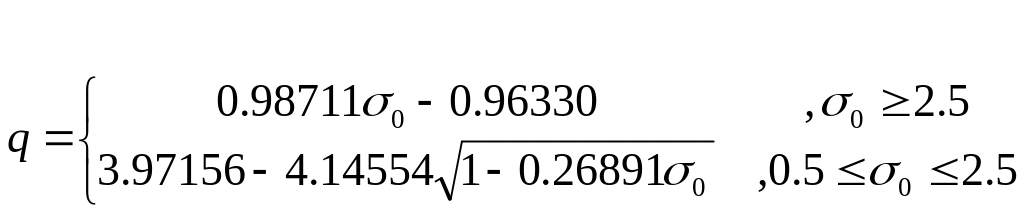Итого сам фильтр сначала применяется
по вертикали, а затем по горизонтали.
Средняя погрешность не превышает
,
что составляет не более 0.68% согласно
[1].
2. Методы параллелизации. OpenCl
Идея распараллеливания вычислений основана на том, что большинство задач может быть разделено на набор меньших задач, которые могут быть решены одновременно. Обычно параллельные вычисления требуют координации действий. Параллельные вычисления существуют в нескольких формах: параллелизм на уровне битов, параллелизм на уровне инструкций, параллелизм данных, параллелизм задач. Параллельные вычисления использовались много лет в основном в высокопроизводительных вычислениях, но в последнее время к ним возрос интерес вследствие существования физических ограничений на рост тактовой частоты процессоров. Параллельные вычисления стали доминирующей парадигмой в архитектуре компьютеров, в основном в форме многоядерных процессоров.
Писать программы для параллельных систем сложнее, чем для последовательных, так как конкуренция за ресурсы представляет новый класс потенциальных ошибок в программном обеспечении, среди которых состояние гонки является самой распространённой. Если при вычислении не применяются циклические (повторяющиеся) действия, то N вычислительных модулей никогда не выполнят работу в N раз быстрее, чем один единственный вычислительный модуль. А так как при реализации фильтра Гаусса применяется в основном циклическая обработка данных, то разумно будет применить один из методов параллелизации.