1.3 Применение фильтра Гаусса с помощью преобразования Фурье

1.3.1 Дискретное преобразование Фурье

Итак, вспомним, что же такое преобразование Фурье – это интегральное преобразование, которое ставит функцию вещественной переменой другую функцию вещественной переменной и может быть записано в виде:

.

Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Не будем перечислять все свойства преобразования, а отметим только важные для нас.

1. Формула обращения позволяет получить искомую функцию

.

2. Теорема о свёртке. Свёртка функций — операция, показывающая «схожесть» одной функции с отражённой и сдвинутой копией другой. Пусть   — две функции вещественной переменной, интегрируемые относительно меры Лебега. Тогда их свёрткой называется функция:

.

Тогда теорема о свёртке гласит: если , тогда

.

Так как мы работаем с изображениями, то представим перечисленные выше высказывания в дискретном виде. Прямое преобразование примет вид:

.

Обратное преобразование:

.

Теорема о свёртке:

.

Таким образом, мы можем выполнить частотную фильтрацию изображения в частотной области. Это означает, что при частотной фильтрации выполняются прямое и обратное пространственно-частотное преобразование, в нашем случае двумерное дискретное преобразование Фурье (ДПФ) преобразует изображение, заданное в пространственной координатной системе (x, y) , в двумерное дискретное преобразование изображения, заданное в частотной координатной системе (u, v). В соответствии с теоремой о свертке, свертка двух функций в пространственной области может быть получена ОДПФ произведения их ДПФ.

Таким образом, алгоритм фильтрации по Гауссу в частотной области будет выглядеть следующим образом:

• выполнить двумерное ДПФ входного изображения f(x,y) (подвергаемого фильтрации) размером (N *M), получить F(u,v);

• вычислить передаточную характеристику фильтра Гаусса в частотной области

,

размер матрицы (N*M); выполнить децентрирование характеристики

H(u,v);

• выполнить поточечное умножение

,

• выполнить ОДФП

На практике ДПФ крайне не эффективно, так как имеет сложность O(N²), поэтому обычно применяют быстрое преобразование Фурье (БПФ).

1.3.2 Быстрое преобразование Фурье

Алгоритм быстрого преобразования Фурье (БПФ) - это оптимизированный по скорости способ вычисления ДПФ. Основная идея заключается в двух пунктах.

1. Необходимо разделить сумму ДПФ из N слагаемых на две суммы по N/2 слагаемых, и вычислить их по отдельности. Для вычисления каждой из подсумм, надо их тоже разделить на две и т.д.

2. Необходимо повторно использовать уже вычисленные слагаемые.

Применяют либо "прореживание по времени" (когда в первую сумму попадают слагаемые с четными номерами, а во вторую - с нечетными), либо "прореживание по частоте" (когда в первую сумму попадают первые N/2 слагаемых, а во вторую - остальные). Оба варианта равноценны. В силу специфики алгоритма приходится применять только N, являющиеся степенями 2. Рассмотрим случай прореживания по времени.

Введём определение поворачивающегося множителя:

.

Определим еще две последовательности: {x_[even]} и {x_[odd]} через последовательность {x} следующим образом:

X_[even]n = X_2n,  X_[odd]n = X_2n+1,

n = 0, 1,..., N/2-1.

Пусть к этим последовательностям применены ДПФ и получены результаты в виде двух новых последовательностей {X_[even]} и {X_[odd]} по N/2 элементов в каждой.

Утверждается, что элементы последовательности {X} можно выразить через элементы последовательностей {X_[even]} и {X_[odd]} по формуле:

 .

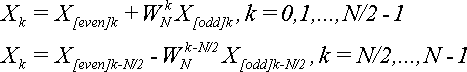Согласно второй части формулы вышеописанной, получим:

 .

ДПФ можно вычислить также по формуле:

.

Также по этой теореме видно, что отпадает необходимость хранить вычисленные X_[even]k и X_[odd]k после использования при вычислении очередной пары и одно вычисление   можно использовать для вычисления двух элементов последовательности {X}.

На этом шаге будет выполнено N/2 умножений комплексных чисел. Если мы применим ту же схему для вычисления последовательностей  {X_[even]} и {X_[odd]}, то каждая из них потребует N/4 умножений, итого еще N/2. Продолжая далее в том же духе log₂N раз, дойдем до сумм, состоящих всего из одного слагаемого, так что общее количество умножений окажется равно (N/2)log₂N, что явно лучше, чем N² умножений по формуле оригинального ДПФ. Если N четно, то это разделение можно продолжать рекурсивно до тех пор, пока не дойдем до двух точечного преобразования Фурье, которое вычисляется по следующим формулам:

.