4.3.2. Метод депозитной книжки

Суть метода. Сумма, положенная на депозит, приносит доход в виде процентов. При снятии с депозита некоторой суммы базовая величина, с которой начисляются проценты, уменьшается. Эта ситуация и имеет место в случае с аннуитетом.

Текущая стоимость аннуитета – это величина депозита с общей суммой причитающихся процентов, ежегодно уменьшающаяся на равные суммы.

Эта сумма годового платежа включает в себя начисленные за очередной период проценты, а также некоторую часть основной суммы долга. Таким образом, погашение исходного долга осуществляется постепенно в течение всего срока действия аннуитета.

Структура годового платежа постоянно меняется: в начальные периоды в нем преобладают начисленные за очередной период проценты. С течением времени доля процентных платежей постоянно уменьшается и повышается доля погашаемой части основного долга.

Интерпретация приведенной стоимости аннуитета с помощью метода депозитной книжки.

Пусть получена ссуда в сумме D₁=S на n лет под процентную ставку r. Сложные проценты начисляются на непогашенный остаток.

Определяем величину годового платежа при возврате долга равными суммами в конце каждого года.

Пусть А – годовой платеж.

В конце первого года часть годового платежа I₁=S*r идет на уплату процентов.

Оставшаяся часть H₁=A-S*r – идет на уплату части долга.

Таким образом на начало второго года величина непогашенного остатка:

D₂=S-(A-S*r)=S(1+r)-A=D₁(1+r)-A.

Аналогично остаток долга на начало k-го года связан остатком долга на начало предыдущего года следующим соотношением:

D_k=D_k-1(1+r)-A, (*)

Из этой формулы:

А=D_k-1*r + (D_k-1 – D_k) – годовой платеж.

где D_k-1*r - проценты, начисляемые на текущий долг,

D_k-1-D_k – сумма, идущая на погашение основного долга.

Если D₁=S, D₂=S(1+r)-A, то

Т.к. долг должен быть выплачен через n лет, то D_n-1=0, т.е. справедливо равенство (k=n+1):

Из этого равенства следует:

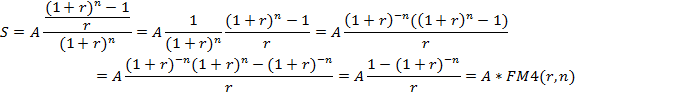
Следовательно S- приведенная стоимость постоянного аннуитета постнумерандо с членом, равным А, т.е.:

I_k=D_k*r – величина процентов за k-й год.

Умножая обе части (*) на r получим:

D_k*r=D_k-1(1+r)r-A*r,

т.е.I_k=I_k-1(1+r)-A*r (**)

Н_k=A-I_k – погашенная часть долга в k-м платеже.

Согласно (**) H_k=A-I_k-1(1+r)+A*r=(A-I_k-1)(1+r).

Таким образом

Н_k=H_k-1(1+r)

Из последней формулы видно, что суммы, идущие на погашение основного долга увеличиваются.

4.3.3. Оценка аннуитета с изменяющейся величиной платежа (переменный аннуитет)

На практике возможны ситуации, когда величина платежа меняется со временем в сторону увеличения или уменьшения.

В таком случае поток платежей представляет собой переменный аннуитет. Для определения будущей или приведенной стоимости аннуитета нужно пользоваться ранее указанными формулами:

Предположим, что имеется аннуитет постнумерандо, платежи которого образуют арифметическую прогрессию с первым членом А и разностью z.

Арифметической прогрессией называется последовательность чисел, в которой каждый член получается из предыдущего путем прибавления к нему одного и того же числа z, которое называется разностью этой арифметической прогрессии.

а, a+z, a+2z, a+3z, … , a+(n-1)z

в этом случае говорят о переменном аннуитете с постоянным абсолютным изменением его членов.

Если число периодов равно n, процентная ставка за базовый период равна r (в соответствие с r один раз в конце периода начисляются сложные проценты) и период аннуитета совпадает с базовым, то наращенный денежный поток (записанный в виде поступления платежей) имеет вид:

A(1+r)^n-1, (A+z)(1+r)^n-2, (A+2z)(1+r)^n-3, .. , (A+(n-2)) z(1+r), A+(n-1)z

Складываем наращенные члены аннуитета и группируем слагаемые, содержащие А и z.

Умножаем обе части равенства (*) на (1+r)

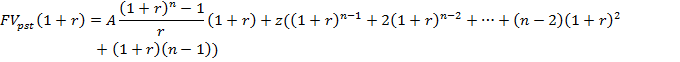
Вычитаем из полученного путем умножения на (1+r) равенства первоначальное равенство (*)

• - -

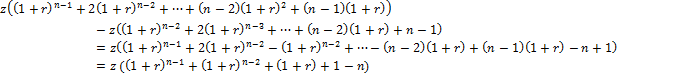
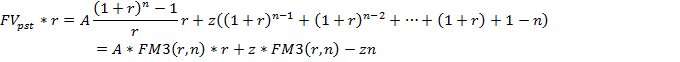
Поделив (**) на (1+r)ⁿ и воспользовавшись равенством получим приведенную стоимость аннуитета

Из формул (**) и (***) можно определить значение любого параметра. Из (**) следует, что

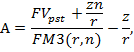
Приведенная стоимость бессрочного аннуитета постнумерандо определяется по формуле (выводится при заданных параметрах n→ , FM4(r, )= из (***):

Пусть платежи в аннуитете постнумерандо образуют геометрическую прогрессию с первым членом А и знаменателем q.

Геометрической прогрессией называется последовательность чисел, в которой каждый член получается из предыдущего путем умножения его на одно и то же число q≠0, называемое знаменателем этой геометрической прогрессии. Геометрическую прогрессию можно записать в виде:

a, aq, aq²,aq³, …

В этом случае говорят о переменном аннуитете с постоянным относительным изменением его членов.

Если r является процентной ставкой за базовый период, совпадающий с периодом аннуитета, n равно числу периодов и в конце каждого периода начисляются сложные проценты, то наращенный денежный поток имеет вид:

А(1+r)^n-1, Aq(1+r)^n-2, …, Aq^n-2(1+r), Aq^n-1

Т.о. наращенный денежный поток представляет собой геометрическую прогрессию с первым членом А(1+r)^n-1 и знаменателем

(проверка правильности определения знаменателя

Сумма членов этой геометрической прогрессии равна:

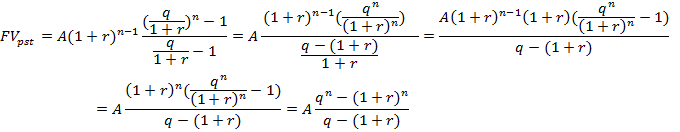
Из этой формулы следует

Формула для определения приведенной стоимости бессрочного аннуитета (при n→ ) имеет вид: