Глава 3. Движение газов в печах

Опыт эксплуатации промышленных печей показывает, что движение газов в них происходит с относительно небольшими скоростями, а давление газов изменяется незначительно и может считаться постоянным. Температура газов в различных зонах печи отличается существенно, но изменяется постепенно при переходе от одной зоны к другой. Это позволяет не учитывать влияния изменения температуры на плотность газов на участках печи небольшой длины. Такой характер движения газов изучается в разделе механики называемом «механика газов» в отличие от раздела «газовая динамика» посвящённого движению газов с большими скоростями, когда существенной становится сжимаемость газов.

3.1. Основные понятия и определения механики газов

Различают идеальные и реальные газы. Идеальные газы это виртуальные газы, не имеющие вязкости. Реальные газы обладают вязкостью, внутренним трением.

3.1.1. Закон Гей-Люссака

Взаимосвязь объёма, плотности и температуры газа выражается законом Гей-Люссака: при постоянном давлении объём газа прямо пропорционален, а плотность обратно пропорциональна температуре.

или: где: (3.1.)

V_t ,м³ и ρ_t, кг/м³ –объём и плотность газа при температуре t ^оС и давлении 0,1013 МПа;

V₀ ,м³ и ρ₀, кг/м³ –объём и плотность газа при 0 ^оС и давлении 0,1013 МПа;

β– температурный коэффициент объёмного расширения, равный 1/273 К^-1

3.1.2. Скорость движения газа

Скоростью движения газа называют объём газа в м³, протекающий через 1 м² сечения канала в секунду, т.е.:

(3.2.)

Размерность этой величины , т. е. такая же, как при движении твёрдых тел.

3.1.3. Уравнение неразрывности газового потока

Газы, движущиеся в каналах печи, не расходуются через сплошные стенки каналов, поэтому при установившемся движении газа по каналу масса газа, проходящая в единицу времени через любое сечение канала, есть постоянная величина.

(3.3.)

Эта формула является выражением закона сохранения массы вещества.

3.1.4. Разновидности давлений газов

Энергию движущегося или покоящегося газа оценивают его давлением. Величина давления газов в печах измеряется U-образными манометрами и выражается в Па (1 миллиметрах водяного столба =9,8 Па).

Потенциальную энергию неподвижного газа, находящегося в сосуде, относительно окружающего воздуха оценивают статическим давлением. Это давление называют также пьезометрическим (рис. 3.1.).

Динамическое или скоростное давление характеризует кинетическую энергию газового потока. Эту энергию вычисляют по формуле:

, где: (3.4.)

-W_t , м/с, и ρ_t, кг/м³ - действительная скорость и плотность газа;

-W₀ , м/с и ρ₀, кг/м³ - скорость и плотность газа, приведённые к 0 ^оС и 0,1013 МПа;

Скоростное давление измеряют дифференциальным манометром (рис. 3.1.). Торец одного конца U-образной трубки расположен параллельно направлению потока, поэтому на поверхность жидкости в нём действует только статическое давление. Торец второго конца трубки манометра расположен навстречу потоку газа, поэтому на жидкость в нём действуют одновременно статическое и скоростное давление.

Разность уровней воды в трубках составляет скоростное давление в масштабе: 1мм в.ст. = 9,8 Па.

Геометрическое давление обусловлено стремлением горячих газов подняться вверх в среде холодных газов. Для объёма газа простой цилиндрической формы эта величина может быть вычислена по расчётной схеме, показанной на рис. 3.2.

Пусть объём газа внутри сосуда заключён между двумя подвижными невесомыми перегородками на уровнях I-I и II-II. Плотность газа внутри сосуда ρ_г меньше плотности воздуха снаружи ρ_в.

p_{в I}

p_{в I}

ρ_г

ρ_в

h

p_{в II}

p_{гII III II}

I

II

p_ст.т.

p _дин.

W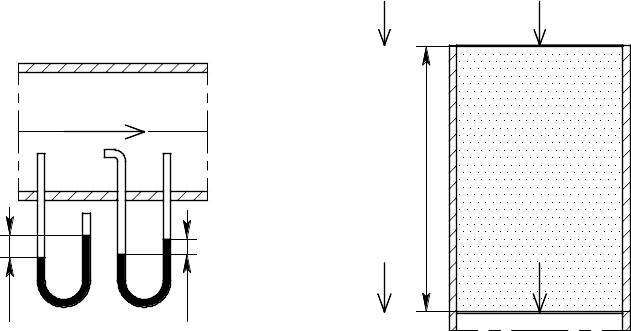

Рис. 3.1. Измерение статического Рис. 3.2. Схема расчёта геометрического

и скоростного давления давления

При этом плотности газа и воздуха не меняются от уровня I-I до уровня II-II (для высоты слоя в пределах 80мм такое условие допустимо).

Давление воздуха на уровне II-II будет равно:

(3.5.)

Давление газа на этом уровне равно:

(3.6.)

Разность этих давлений и называется геометрическим давлением:

, Па (3. 7.)

Под действием этого давления газ, заключённый между перегородками, стремится подняться вверх. Если верхнюю перегородку закрепить, нижняя перегородка будет пониматься, сжимая газ, до тех пор, пока его плотность не сравняется с плотностью воздуха.