
- •Терези.
- •Правила користування технічними терезами:
- •Штангенциркуль.
- •М ікрометр.
- •Методика і порядок вимірів
- •Теоретичні відомості та опис приладів.
- •Увага: При виконанні роботи слідкувати, щоб вантажі були добре закріплені.
- •Іі. Вивчення биття
- •Теоретичні водомості
- •Рівняння хвилі має вигляд:
- •Опис установки.
- •2. Теоретичні відомості та опис установки
- •3. Виведення розрахункової формули
- •4. Порядок виконання роботи
- •4.6 Визначити значення коефіцієнта в'язкості за формулою (3.9).
- •Продовження таблиці 4.1
Іі. Вивчення биття
Прилади і матеріали: 1) електронний осцилограф СІ- 1; 2) два звукових генератори ГЗ-18; 3) два гучномовці ІГД— 18; 4) мікрофон; 5) низькочастотний підсилювач.
Теоретичні відомості та опис приладів
Розглянемо
результат додавання двох однаково
напрямлених коливань
![]() і
і
![]() з близькими частотами
з близькими частотами
![]() і
і
![]() .
Для спрощення покладемо, що початкові
фази цих коливань однакові, тобто
.
Для спрощення покладемо, що початкові
фази цих коливань однакові, тобто
![]() .
Нехай амплітуди цих коливань
.
Нехай амплітуди цих коливань
![]() і
і
![]() .
Тоді
.
Тоді
![]() ;
;
![]() .
.
Додавання
цих коливань можна здійснити
графічним методом. Покладемо, що вектори
амплітуд
та
коливань, що додаються, обертаються
(рис. 71) з різними кутовими швидкостями
і
.
В результаті цього кут між векторами
і
змінюватиметься з часом. Це приведе до
зміни результуючої амплітуди. Покладемо,
що
![]() .
Тоді різниця фаз цих коливань дорівнюватиме
.
Тоді різниця фаз цих коливань дорівнюватиме
![]() .
Як бачимо, різниця фаз цих коливань
залежить від часу. З
.
Як бачимо, різниця фаз цих коливань
залежить від часу. З
![]() (рис. 71) знаходимо амплітуду
результуючого коливання
(рис. 71) знаходимо амплітуду
результуючого коливання
![]() .
(1)
.
(1)
Як видно з (1), амплітуда результуючого коливання залежить від часу.
З того, що вектор амплітуди результуючого коливання на діаграмі (рис. 71) обертається із змінною кутовою швидкістю, можна зробити висновок, що результуюче коливання не є гармонічним.
Припустимо,
що амплітуди складових коливань
дорівнюють одна одній, тобто
![]() ,
а циклічні частоти трохи відрізняються.
Тоді з (1) дістанемо
,
а циклічні частоти трохи відрізняються.
Тоді з (1) дістанемо
![]() .
.
Звідси
![]() .
.
За векторною діаграмою знайдемо, що зміщення в результуючому коливанні
![]() (2)
(2)
З (2) можна
зробити висновок, що в результаті
додавання двох коливань з однаковими
початковими фазами і амплітудами, а
також близькими періодами утворюється
нове коливання з циклічною частотою
![]() і амплітудою
і амплітудою![]() ,щоповільно
змінюється з часом. Таке явище називається
биттям.
,щоповільно
змінюється з часом. Таке явище називається
биттям.
У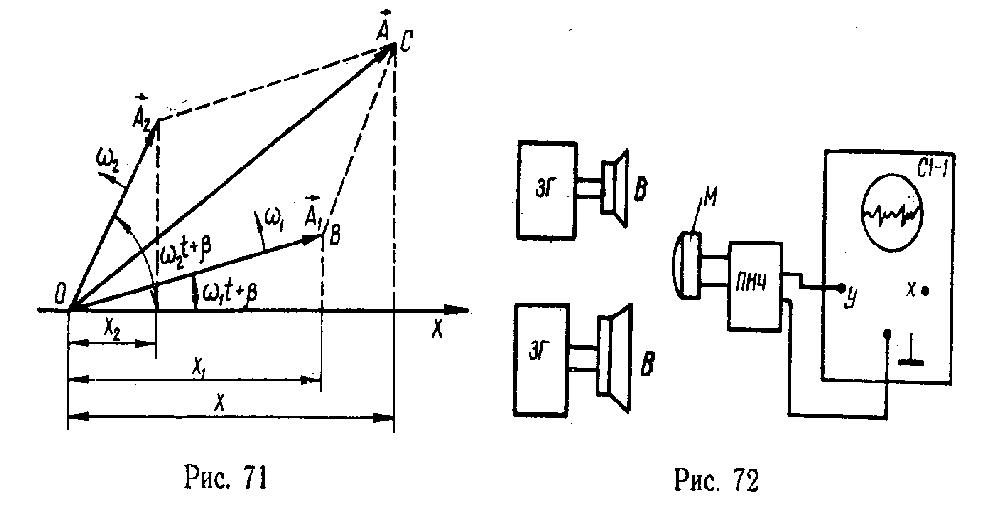 становка
(рис. 2) складається з електронного
осцилографа, мікрофона М, гучномовців
В, двох звукових генераторів ЗГ та
підсилювача низької частоти ПНЧ.
становка
(рис. 2) складається з електронного
осцилографа, мікрофона М, гучномовців
В, двох звукових генераторів ЗГ та
підсилювача низької частоти ПНЧ.
Рис. 1 Рис. 2
Джерелами звукових коливань з близькими частотами є гучномовці. Звукові коливання надходять до мікрофона, за допомогою якого відбувається перетворення їх в електричні коливання синусоїдної форми тих самих частот. Утворені електричні коливання підсилюються ПНЧ і подаються на вертикально відхиляючі пластини електронно-променевої трубки осцилографа.
Таким чином, електронний промінь трубки бере участь удвох коливаннях одного напряму з близькими частотами і однаковими амплітудами. Графік результуючого коливання електронного променя спостерігаємо на екрані електронного осцилографа.
Порядок виконання роботи
1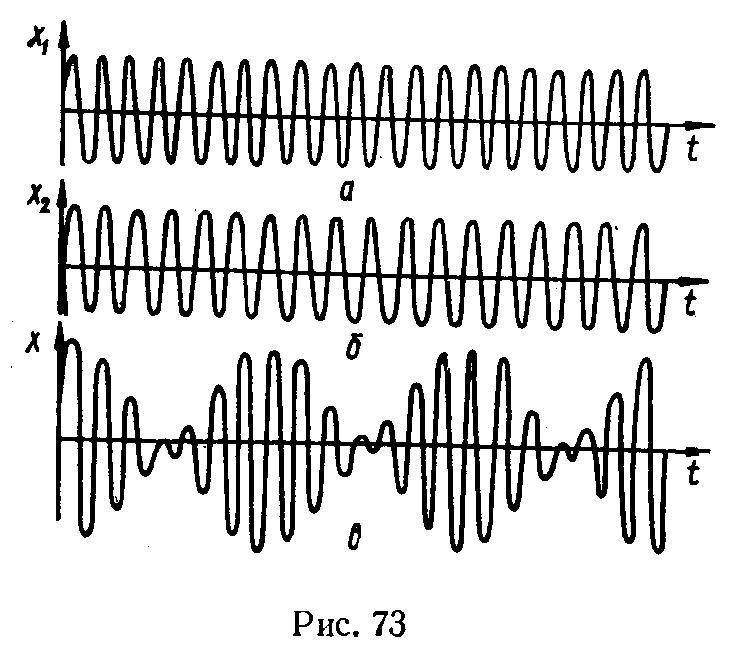 .
Увімкнути електронний осцилограф,
підсилювач та один звуковий генератор
і дати їм прогрітись протягом 2—3 хв.
.
Увімкнути електронний осцилограф,
підсилювач та один звуковий генератор
і дати їм прогрітись протягом 2—3 хв.
2. По шкалі звукового генератора встановити відповідну частоту (її величину задає керівник занять) і добитись на екрані осцилографа стійкого зображення графіка, одержуваного від гучномовця звукового коливання (рис. 3,а).
Рис. 3
3. Вимкнути перший генератор і ввімкнути другий. Встановити на шкалі цього генератора частоту , що на 1—2 Гц відрізняється від частоти першого генератора.
4. Добитись стійкого зображення на екрані осцилографа графіка другого гармонічного коливання (рис. 3,б).
5. Одночасно ввімкнути обидва генератори і добитись стійкого зображення биття на екрані осцилографа (рис. 3,в).
6. Зарисувати з екрана осцилографа графіки складових коливань та биття.
? Контрольні запитання і завдання
1. Сформулюйте закон зміни амплітуди результуючого коливання, що його дістають від додавання коливань одного напряму та близьких частот.
2. Що таке биття?
Лабораторна робота № 10
Вивчення додавання взаємно перпендикулярних коливань однакової частоти.
Прилади і матеріали: 1) електронний осцилограф; 2) два звукові генератори.
Теоретичні відомості та опис установки
Матеріальна
точка бере участь у двох взаємно
перпендикулярних коливаннях з частотами
![]() і
і
![]() :
:
![]() ;
(1)
;
(1)
![]() ,
(2)
,
(2)
де - початкова різниця фаз між коливаннями.
Щоб знайти траєкторію точки, яка бере одночасно участь у двох взаємно перпендикулярних коливаннях, з рівнянь (1) і (2) виключимо час t. Для цього праві і ліві частини цих рівнянь поділимо відповідно на і . Дістанемо
![]() ,
(3)
,
(3)
![]() .
(4)
.
(4)
З формули (4) випливає, що
![]() .
(5)
.
(5)
З урахуванням (3), а також умови
![]()
для різних значень n формула (5) набуває вигляду:
а)
![]()
![]() ;
(6)
;
(6)
б)
![]()
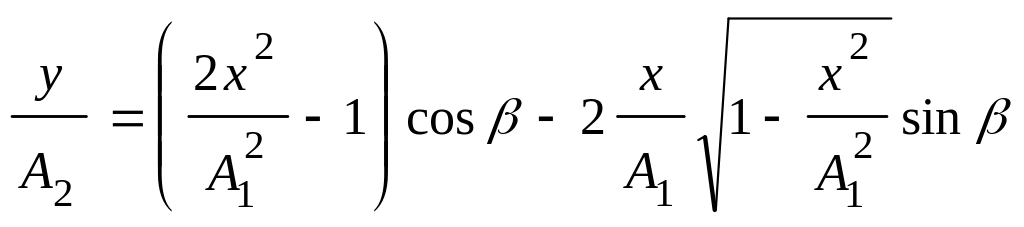 .
(7)
.
(7)
Для
![]() непарних цілих чисел,
непарних цілих чисел,
![]() ,
маємо
,
маємо
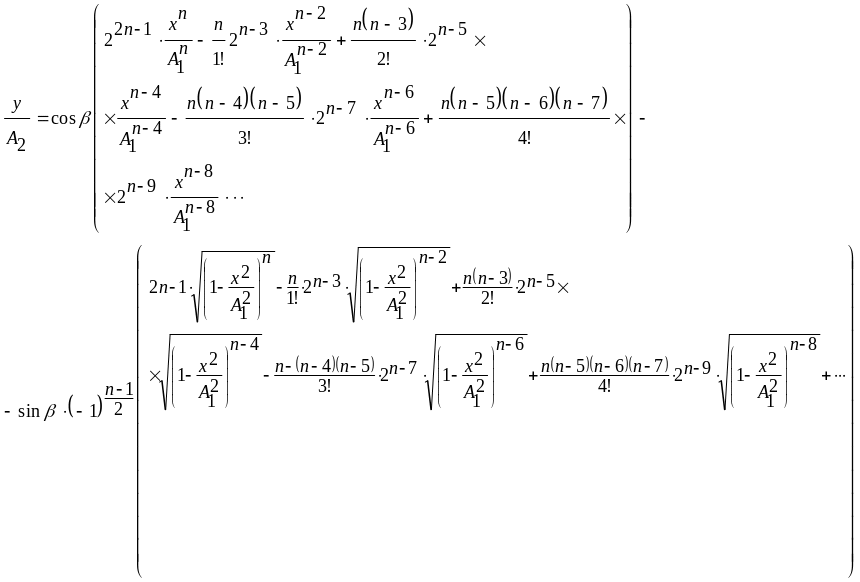 (8) Для
парних цілих чисел,
,
маємо
(8) Для
парних цілих чисел,
,
маємо
 (9)
(9)
Р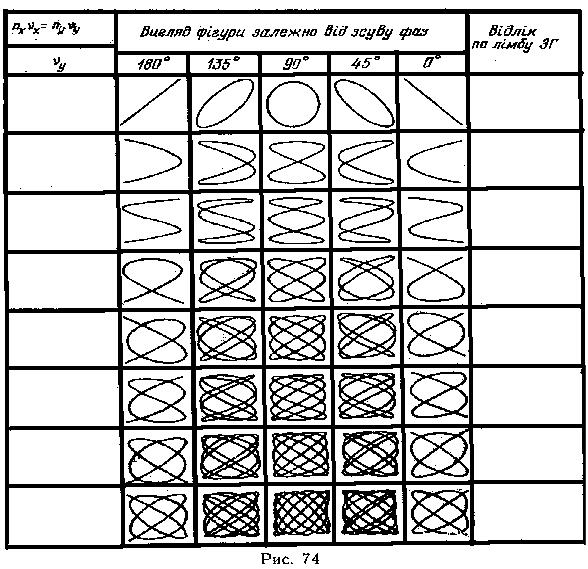 івняння
(6) — (9) є рівняннями траєкторій точки,
що бере участь одночасно у двох взаємно
перпендикулярних коливаннях. Залежно
від співвідношення частот складових
коливань ці криві набувають тієї чи
іншої форми. Їх називають фігурами
Ліссажу. Найпростіша форма траєкторій
буде при
.
Справді, перетворимо формулу (6) так:
івняння
(6) — (9) є рівняннями траєкторій точки,
що бере участь одночасно у двох взаємно
перпендикулярних коливаннях. Залежно
від співвідношення частот складових
коливань ці криві набувають тієї чи
іншої форми. Їх називають фігурами
Ліссажу. Найпростіша форма траєкторій
буде при
.
Справді, перетворимо формулу (6) так:
![]() .
.
Піднісши обидві частини цієї рівності до квадрата, дістанемо
.
![]() (10)
(10)
Звідси видно, що траєкторія результуючого руху являє собою еліпс. Отже, якщо точка бере участь у двох взаємно перпендикулярних коливаннях однакової частоти , то в загальному випадку дістанемо рух по еліпсу. Причому орієнтація цього еліпса відносно осей Ох і Оу залежить від різниці фаз складових коливань.
В окремих випадках еліпс може вироджуватись у пряму або коло. Спинимося на розгляді деяких окремих випадків.
1. Нехай
![]() .
Формула (10) набуває вигляду
.
Формула (10) набуває вигляду
![]() ,
(11)
,
(11)
звідки
![]() .
.
Отже,
при різниці фаз, що дорівнює нулю,
траєкторія точки є пряма, що проходить
через початок координат і утворює з
віссю
![]() кут, тангенс якого дорівнює
кут, тангенс якого дорівнює
![]() .
.
2. При
різниці фаз
![]() рівняння траєкторії має такий вигляд:
рівняння траєкторії має такий вигляд:
![]() .
.
Звідси
![]() або
або
![]() .
.
Отже,
знову маємо траєкторію, яка являє собою
пряму, нахилену до осі Ох, але вже під
кутом, більшим від
![]() .
.
3 .
При різниці фаз складових коливань
.
При різниці фаз складових коливань
![]() або
або
![]() рівняння траєкторії має вигляд
рівняння траєкторії має вигляд
![]() .
.
Рис. 2
В
розглядуваному випадку точка рухається
по еліпсу, осі якого збігаються з осями
координат. Якщо
![]() ,
то рівняння траєкторії буде рівнянням
кола з радіусом, що дорівнює А, тобто
,
то рівняння траєкторії буде рівнянням
кола з радіусом, що дорівнює А, тобто
![]() .
При
.
При
![]() криві матимуть складнішу форму. Фігури
Ліссажу наведено на рис. 1. При вивченні
додавання двох взаємно перпендикулярних
коливань за загальним виглядом фігур
Ліссажу можна визначити частоту одного
складового гармонічного коливання,
якщо відома частота іншого.
криві матимуть складнішу форму. Фігури
Ліссажу наведено на рис. 1. При вивченні
додавання двох взаємно перпендикулярних
коливань за загальним виглядом фігур
Ліссажу можна визначити частоту одного
складового гармонічного коливання,
якщо відома частота іншого.
Установка
складається з двох звукових генераторів
та електронного осцилографа (рис. 2). На
вхід «X» блока горизонтально відхиляючих
(вертикально розташованих) пластин
осцилографа подають від одного генератора
синусоїдну напругу відомої частоти
![]() .
Від другого генератора на вхід «Y» блока
вертикально відхиляючих пластин подають
синусоїдну напругу невідомої частоти
.
Від другого генератора на вхід «Y» блока
вертикально відхиляючих пластин подають
синусоїдну напругу невідомої частоти
![]() .
Залежно від співвідношення цих частот
.
Залежно від співвідношення цих частот
![]() (12)
(12)
і зсуву фаз обох складових коливань на екрані осцилографа утворюється та чи інша фігура Ліссажу.
Порядок виконання роботи
1. Скласти установку за схемою (рис. 2).
2. Вимкнути генератор розгортки осцилографа. Для цього потрібно ручку «Диапазон частот», що розташована на передній панелі осцилографа, поставити в положення «Вьікл.».
3. Поставивши ручки «Усиление по оси X» та «Усиление по оси У» в нульові положення, добиваються мінімального підсилення змінної напруги, що подається від генераторів на пластини електронно-променевої трубки осцилографа. Ручку звукового генератора «Амплитуда» встановлюють на поділці «0».
4. По шкалах правого звукового генератора встановлюють частоту (значення цієї частоти задає керівник занять).
5. Увімкнути електронний осцилограф і генератори та дати їм прогрітись протягом 2. — 3 хв. Світлову пляму виводять на середину екрана осцилографа і фокусують.
6. За допомогою ручки осцилографа «Усиленне по оси X» добиваються тонкої горизонтальної смуги на екрані. Довжина смуги має дорівнювати приблизно половині діаметра екрана.
7. Обертанням ручки звукового генератора «Амплитуда» добитись появи на екрані осцилографа фігури Ліссажу. Встановити її симетрично відносно координатних осей.
8. На міліметровий папір змалювати з екрана осцилографа одержану фігуру Ліссажу і координатну сітку.
9.
Підрахувати кількість точок
![]() перетину фігури Ліссажу з віссю Ох та
з віссю Оу (
перетину фігури Ліссажу з віссю Ох та
з віссю Оу (![]() ).
).
Якщо вісь координат проходить через точку перетину віток кривої, її рахують двічі. Така точка відповідає кратним кореням рівняння траєкторії.
10. Для знаходження частоти досліджуваного гармонічного коливання рівняння (12) запишемо у вигляді
![]() .
(12а)
.
(12а)
Знайдену кількість точок і підставити в це рівняння і обчислити шукану частоту.
Зафіксувати
поділку
![]() шкали правого звукового генератора,
якій відповідає здобуте значення
.
шкали правого звукового генератора,
якій відповідає здобуте значення
.
11. Змінюючи частоту звукового генератора, добитись стійкого зображення нової фігури Ліссажу і знайти . Зафіксувати поділку шкали. Вимірювання провести для кількох фігур Ліссажу, наведених на рис. 74. Проти поділок на лімбі генератора досліджуваних коливань поставити відповідні значення частот.
12. За формою фігур Ліссажу, наведених на рис. 74, і відношенням частот складових коливань знайти різницю фаз цих коливань.
? Контрольні запитання
1. Що називають фігурами Ліссажу?
2. Які фігури утворюються при накладанні двох взаємно перпендикулярних коливань з однаковими частотами?
3. Чому одному і тому самому відношенню частот відповідає ряд фігур?
Лабораторна робота 11
Визначення швидкості поширення звуку фазовим методом.
Обладнання: установка для вивчення звукових хвиль, осцилограф.
