Увага: При виконанні роботи слідкувати, щоб вантажі були добре закріплені.

3. Обчислити момент інерції маятника за формулою (15).

4. Штангенциркулем виміряти діаметр шківа в різних місцях і обчислити його середнє значення.

5. Відстань h, що проходить тягарець m при опусканні, задається викладачем.

6. Намотуючи нитку на шків, підняти вантаж m у верхнє положення.

7. Провести вимірювання часу опускання вантажу t

8. Дослід повторити тричі і обчислити середнє значення t_c.

9. Визначити момент інерції за формулою (22).

10. Оцінити відносні та абсолютні похибки результатів.

11. Результати лабораторної роботи занести в таблиці 1 і 2:

Таблиця 1

m1 10-3кг	∆m1 10-3кг	L 10-3м	∆l 10-3м	m2 10-3 кг	∆m2 10-3кг	R 10-3м	∆R 10-3м	l, 10-2 кг*м2	∆l, 10-2 кг*м2	%

Таблиця 2

№ п/п	m 10-3кг	∆m 10-3кг	d 10-3м	∆d 10-3м	t, c	∆t c	h 10-3м	∆h 10-3м	J 10-2 кг*м2	∆J, 10-2 кг*м2	%
1
2
3
С.з.

12. Результат роботи подати у вигляді . (для обох способів розрахунку), вказуючи також величини відносних похибок

? Контрольні запитання і завдання.

1. Дати означення моменту сили та вказати одиниці вимірювання.

2. Дати означення моменту інерції та вказати одиниці вимірювання.

3. Сформулювати основний закон динаміки обертального руху твердого тіла.

4. Обґрунтувати положення: момент інерції є міра інертності твердого тіла при обертальному русі.

5. При яких положеннях тягарців момент інерції маятника Обербека буде максимальним? мінімальним?

6. Вивести формули для розрахунку похибок.

Лабораторна робота № 6

Визначення моменту інерції махового колеса динамічним методом.

Прилади і матеріали: 1) махове колесо; 2) секундомір; 3) тягарець невеликої маси; 4) масштабна лінійка з міліметровими поділками; 5) технічні терези.

Теоретичні відомості та опис приладів

Момент інерції махового колеса визначають на установці, яка складається махового колеса 2 зі шківом 1, насадженого на вал АВ, лінійки і тягарця 3 (рис.1). Вал закріплений у двох підшипниках. На шків 1 намотується нитка. До її кінця прикріплюють тягарець з масою m.

Рис.1

Під дією тягарця шків разом з валом і маховим колесом рівно прискорено обертається. На характер обертального руху впливають значення моменту інерції махового колеса, моменту інерції шківа, моменту інерції вала та сили тертя в підшипниках. Вал і шків вибирають такими, щоб вони мінімально впливали на характер обертального руху і не вносили істотних змін в його характер. При падінні тягарця Р його потенціальна енергія mgh, де h – висота підняття тягарця, перетворюється в кінетичну енергію поступального руху тягарця, в кінетичну енергію обертального руху махового колеса і витрачається на виконання роботи подолання сил тертя. Кінетична енергія поступального руху тягарця визначається за формулою:

.

Кінетична енергія обертального махового колеса визначається за формулою:

Робота подолання сил тертя дорівнює , де А – робота, виконана за один оберт; – кількість обертів маховика. Отже

(1)

В момент, коли тягарець повністю опустився, нитка спадає до шківа і колесо робить обертів до повної зупинки. За обертів виконання робота подолання сил тертя, яка дорівнює Ця робота виконується за рахунок кінетичної енергії обертального руху колеса, яку воно в момент спадання нитки:

(2)

Робота подолання сил тертя в підшипниках за один оберт з рівняння (2):

(3)

Підставивши (3) в (1), матимемо:

.

Визначимо і через висоту падіння тягарця h і час його падіння t:

, ,

де r– радіус шківа. Тоді момент інерції махового колеса:

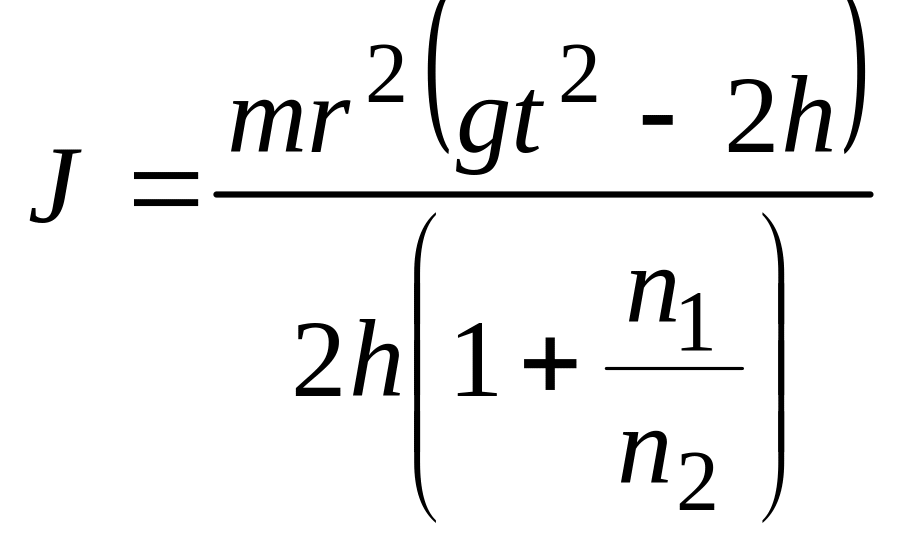. (4)

Якщо нитка одним кінцем прикріплена до вала махового колеса, то за законом збереження і перетворення енергії маємо:

, (5)

де A=Fh – робота подолання сил тертя; F – сили тертя. Силу тертя визначимо з таких міркувань. Обертаючись за інерцією, махове колесо підніме тягарець на висоту , система матиме потенціальну енергію . Різниця потенціалів енергій дорівнюватиме роботі подолання сил тертя , звідки:

Підставивши вирази для , , F в рівняння (5), матимемо формулу для визначення моменту інерції махового колеса для цього випадку:

(6)

Порядок виконання роботи

1. Визначити на технічних терезах масу тягарця. Виміряти радіус шківа штангенциркулем.

2. Намотати на шків нитку. Прикріпити тягарець до другого кінця нитки.

3. Наклеїти на маховик кольоровий папірець, щоб легше було визначити кількість обертів маховика. Виміряти відстань від нижньої основи тягарця до площадки, на яку опускається тягарець.

4. Виміряти час, протягом якого тягарець пройшов відстань h. Обчислити кількість обертів n махового колеса від початку руху до повної його зупинки.

5. Визначити кількість обертів колеса під дією тягарця P за формулою , де h – шлях, який пройшов тягарець, діючи на шків, r– радіус шківа. Кількість обертів махового колеса від моменту припинення дії тягарця (від моменту удару тягарця об площадку) і до повної зупинки його дорівнює різниці між кількістю обертів від початку руху колеса до повної зупинки і кількістю обертів колеса під дією тягарця, тобто . Добуті експериментально значення величин n, n₂, h, t підставити в формулу (4) і обчислити момент інерції махового колеса. Щоб результат був задовільний, треба повторити вимірювання 7-10 разів.

6. Закріпити один кінець нитки завдовжки h до шківа і намотати її на нього. До другого кінця нитки прикріпити тягарець.

7. Одночасно ввімкнути секундомір і відпустити тягарець. Визначити час опускання тягарця t (час від початку руху колеса до моменту дотику тягарця до площадки).

8. Виміряти висоту піднімання тягарця при обертанні колеса за інерцією. За формулою (6) обчислити момент інерції махового колеса. Порівняти значення J, знайденні з формул (4) і (6). Вивести формули для обчислення відносної і абсолютної похибок і визначити їх.

? Контрольні запитання і завдання.

1. Звідки випливає, що момент інерції є величина адитивна?

2. Вкажіть раціональний спосіб обчислення моменту інерції тіл з отворами.

3. Чим характерна певна вісь з множини паралельних осей, відносно якої момент інерції твердого тіла мінімальний.

Лабораторна робота № 7

Визначення прискорення сили тяжіння за допомогою математичного маятника.

Мета: Ознайомлення на досліді з законами коливання математичного маятника та визначення за його допомогою прискорення сили тяжіння.

Оладнання: Математичний маятник, секундомір, масштабна лінійка.

Основні теоретичні відомості.

Падіння тіл на Землі - один з проявів закону всесвітнього тяжіння, відкритого І.Ньютоном. Згідно з законом всесвітнього тяжіння, сила взаємодії двох матеріальних точок з масами m₁ і m₂ на віддалі R визначається рівнянням:

F=m₁m₂/R² (1)

де =6.6710^-11 - гравітаційна стала.

Дослідження, проведені ще Ньютоном, показали, що в даному місці на Землі всі тіла падають з однаковим прискоренням. На основі закону всесвітнього тяжіння, воно повинно дорівнювати:

g=M/R² (2)

де: M-маса Землі, R- радіус Землі для даного місця.

Визначення прискорення сили тяжіння дало можливість обчислити масу Землі і середню її густину: M=5,96∙10²⁴ кг; =5.5∙10³ кг/м³.

Збільшення прискорення сили тяжіння при переміщенні від екватора до полюсів показало, що Земля має форму еліпсоїда. Прискорення на широті 45 g=9,80665 м/с² домовились називати нормальним прискоренням.

Земна кора в різних місцях має неоднаковий склад. Тому в місцях, де кора має більшу густину, прискорення збільшується. Це послужило засобом для розвідування корисних копалин.

За законом всесвітнього тяжіння в міру віддалення від Землі прискорення зменшується обернено пропорційно квадрату віддалі від центра Землі. Це зменшення стає істотним і береться до уваги при обчислені рухів штучних космічних тіл.

Одним із засобів визначення прискорення вільного падіння тіл є математичний маятник.

Математичним маятником називається матеріальна точка, підвішена на довгій, тонкій, нерозтяжній нитці, масою якої можна знехтувати.

Моделлю математичного маятника може служити тягарець, підвішений на довгій (l>>r_т) мало розтяжній нитці, масою якої можна знехтувати порівняно з масою тягарця (m_н<<m_т).

Коливання математичного маятника відбувається під дією сили тяжіння. Коли маятник перебуває в положенні рівноваги, то сила тяжіння зрівноважується силою пружності нитки. Якщо маятник відхилити на кут  (рис.1), то сила пружності нитки буде зрівноважувати лише одну складову сили тяжіння F₁ , яка напрямлена вздовж нитки, друга ж складова F₂, напрямлена до положення рівноваги, залишається незрівноваженою і є тією силою, під дією якої відбувається коливання маятника.

Рис.1 Рис.2

Як видно з рис. 1. ця сила дорівнює:

F₂= −Psin або F₂= −Рх/l (3)

При малих кутах відхилення (10-15), коли можна замінити синус кута тангенсом маємо sin tgх/l

Тут Р -вага кульки l -довжина нитки, х- величина зміщення кульки від положення рівноваги.

Сила F₂ завжди напрямлена проти зміщення х, тобто є повертаючою силою.

З виразу (3) випливає, що повертаюча сила F₂ пропорційна зміщенню х. Під дією сили, пропорційної до зміщення і напрямленої до положення рівноваги, виникають, як відомо, гармонійні коливання, тобто коливання, які описуються рівняннями синусоїди або косинусоїди:

х=Аsint (4)

де х-величина зміщення коливної точки від положення рівноваги в даний момент часу; А-амплітуда коливань (найбільше відхилення коливної точки від положення рівноваги);

ω=2/Т — циклічна частота (ця величина показує число повних коливань за час 2 секунд);

Т-період коливань;

t-час;

t-фаза коливання.

На основі другого закону Ньютона можна записати:

F₂= ma, а P= mg,

тоді рівність (3) прийме вигляд:

і (5)

де m— маса кульки,

a — прискорення, якого набуває кулька під дією повертаючої сили,

g — прискорення сили тяжіння.

З другого боку, вираз для прискорення кульки можна одержати з рівняння (4), маючи на увазі, що прискорення є другою похідною від зміщення по часу:

(6)

Оскільки Asint=x, то (6-а)

З рівностей (5) і (6-а) отримуємо:

. Звідки (7)

З цього співвідношення можна визначити прискорення сили тяжіння шляхом вимірювання довжини маятника l і періоду його коливань Т. Але безпосереднє вимірювання довжини маятника пов’язане з деякими незручностями, тому вдаються до вимірювання різниці довжин l₁ і l₂, яким відповідають періоди коливань Т₁ і Т₂.

Так, застосовуючи формулу (7) для маятників, довжини яких l₁ і l₂, періоди коливань відповідно дорівнюють Т₁ і Т₂, можна записати:

і

Якщо піднести обидва вирази до квадрату і відняти другий вираз від першого, то одержимо:

, звідки (8)

За початок відліку приймемо яку-небудь горизонтальну поверхню, наприклад, поверхню стола або підлоги. Оскільки віддаль від точки підвісу маятника до вибраного нульового рівня ― величина стала, то можна записати:

де d — довжина тягарця;

h₁ і h₂ — віддалі від нижньої точки тягарця до початку відліку (Рис2).

З останньої рівності одержимо:

l₁-l₂=h₂-h₁.

Тоді формулу (8) можна записати у вигляді:

(9)

Віддалі h₁ і h₂ нижньої точки тягарця від поверхні стола (підлоги) з достатньою точністю можна виміряти за допомогою штангенрейсмуса (вертикально встановлена на спеціальній підставці лінійка з ноніусом). При відсутності штангенрейсмуса можна скористатись масштабною лінійкою з міліметровою шкалою.

Необхідно відмітити, що формула (9) може дати значну похибку у визначенні g , якщо різниця h₂-h₁ дуже мала, тобто, якщо будуть близькими значення періодів T₁ і T₂ коливань маятника. Тому при виконанні роботи необхідно встановити такі довжини маятника, щоб різниця h₁-h₂ була великою.

Порядок виконяння роботи.

1. Встановити максимально можливу довжину маятника і виміряти віддаль h₁ від нижньої точки тягарця до вибраної поверхні.

2. Відхилити маятник на невеликий кут (10-15) і визначити час за який маятник здійснить n повних коливань (n=50100).

3. Визначити період коливань Т₁=t₁/n. Визначення періоду коливань проводять декілька разів і знаходять його середнє значення Т_1(сер).

4. Зменшити довжину підвісу маятника і виміряти віддаль h₂ від нижньої точки тягарця до поверхні підлоги. Потім аналогічно до пунктів 2 і 3 обчислити період Т₂=t₂/n і Т_2(сер).

5. Результати вимірювань і обчислень записати в таблицю 1.

6. Повторити дослід ще два рази, змінюючи віддаль h₂.

7. Результати вимірювань і обчислень записати в таблиці 2 і 3.

8. Знайти середнє значення прискорення сили тяжіння за формулою

9. На основі робочої формули одержати формулу для обчислення відносної похибки. Обчислити відносну та абсолютну похибки визначення прискорення сили тяжіння. Абсолютні похибки h₁ i h₂ визначити за приладом, яким вимірювалась віддаль h₁ i h_2. Значення абсолютних похибок T_1(ср) i T_2(ср) обчислити за формулою T=t/n, де за t взяти половину ціни поділки секундоміра.

10. Кінцевий результат записати у вигляді:

g=g_срg_ср;

.

ТАБЛИЦЯ 1

№	n	h1= відповідає довжині l1			h2= відповідає довжині l2			g	g	gср/gср
		T1	T1	T1	t2	T2	T2
1.
2.
3.
Сер.

ТАБЛИЦЯ 2

№	n	h1= відповідає довжині l1			h2= відповідає довжині l2			g	g	gср/gср
		T1	T1	T1	t2	T2	T2
1.
2.
3.
сер.

ТАБЛИЦЯ 3

№	n	h1= відповідає довжині l1			h2= відповідає довжині l2			g	g	gср/gср
		T1	T1	T1	t2	T2	T2
1.
2.
3.
сер.

11. Зробити висновки.

? Контрольні запитання.

1. Що називається математичним маятником?

2. Що називається періодом, фазою, циклічною частотою і в яких одиницях ці величини вимірюються?

3. Записати рівняння гармонійного коливання, швидкості і прискорення коливної точки.

4. Вивести формулу для періоду коливання математичного маятника.

5. Від чого залежить прискорення сили тяжіння Землі?

6. Рівняння коливання матеріальної точки задано у вигляді

7. Записати вираз для визначення повної енергії коливної точки.

За яку частину періоду тіло, яке здійснює гармонійні коливання, проходить весь шлях від середнього положення до крайнього? Першу половину шляху? Другу половину.

Лабораторна робота № 8

Застосування фізичного маятника для визначення прискорення вільного падіння.

Прилади і матеріали:1) фізичний маятник;2) шкала;3) секундомір.

Теоретичні відомості та опис приладів

Із закону всесвітнього тяжіння випливає, що на тіло, яке знаходиться на висоті h над поверхнею Землі, діятиме сила, рівна за величиною:

,

де величина g називається прискоренням вільного падіння, Нм²кг^-2 - гравітаційна стала, m - маса тіла, М- маса Землі (M=5,98·10²⁴ кг), R₃ - радіус Землі. У векторній формі сила тяжіння:

.

i спрямовані до центра Землі. Для тіла, що знаходиться біля поверхні Землі h<<R₃ (R₃=6,37*10⁶м)

Величина прискорення вільного падіння залежить від широти місцевості: на екваторі прискорення вільного падіння рівне g=9,780 м/с², на полюсі -g=9,832 м/с².

У даній роботі величина g визначається дослідним шляхом за допомогою фізичного маятника. Фізичний маятник - тіло, що коливається під дією сили тяжіння навколо горизонтальної осі, що не проходить через центр мас. В даній роботі в якості фізичного маятника використовується стержень (рис. 1), що коливається відносно горизонтальної осі, яка проходить через кінець стержня.

Сума кінетичної і потенціальної енергії фізичного маятника:

,

де J - момент інерції маятника відносно осі обертання, який визначається за теоремою Штейнера, - кутова швидкість маятника , m- маса маятника, g прискорення вільного падіння біля поверхні Землі, L - віддаль від осі обертання до центра мас, - кут відхилення маятника від положення рівноваги; потенціальну енергію відраховуємо від положення стійкої рівноваги маятника. Продиференціюємо (4) по часу:

.

Оскільки , а кутове прискорення , то замість (5) маємо:

.

Поділимо обидві сторони рівняння (6) на J і введемо позначення:

і розглянемо випадок малих відхилень від положення рівноваги ( ). Тоді замість (7) отримуємо:

Розв'язком рівняння (8) є :

,

де α₀ - максимальний кут відхилення маятника від положення рівноваги (амплітуда коливань), - кутова частота, - початкова фаза (якщо в початковий момент часу маятник максимально відхилений від положення рівноваги, =0).

Період коливань фізичного маятника:

.

З формули (9) можна визначити прискорення вільного падіння:

,

Вимірявши на досліді період коливань стержня та визначивши його момент інерції відносно кінця.

Рис.1

Досліджуваний маятник - це стержень з масою m і довжиною l. Для нього момент інерції відносно осі, що проходить через центр маси, визначається за формулою:

.

Mомент інерції відносно осі, що проходить через верхній кінець, визначається за теоремою Штейнера:

,

а віддаль від осі обертання до центра маси:

.

З формули (10), враховуючи вирази (11)-(13), можна визначити прискорення вільного падіння:

Це є розрахункова формула для визначення прискорення вільного падіння.

Порядок виконання роботи.

1. Визначити довжину стержня l.

2. Визначити період коливань фізичного маятника Т. Для цього секундоміром виміряти час t певного числа п коливань (й задає викладач) і підставити ці дані в формулу:

3. Повторити дослід 3 рази. Знайти середнє значення Т.

4. Обчислити значення прискорення вільного падіння за формулою (14).

5. Оцінити відносну і абсолютну похибки.

6. Результат роботи подати у вигляді g = g_c ± g_c, вказуючи також величини відносної похибки .

7. Результати лабораторної роботи занести в таблицю 1:

Таблиця 1

№ п/п	l, м	l, М	T, c	T, c	g, м/с2	g, м/с2	%
1
2
3
С.з.

? Контрольні запитання і завдання.

1. Сформулювати закон всесвітнього тяжіння.

2. З'ясувати фізичний зміст прискорення вільного падіння тіл.

3. Що таке фізичний маятник?

4. Записати вирази для моменту сили та моменту інерції в даній роботі.

5. Записати рівняння гармонічного коливання.

6. Що таке амплітуда, період, частота, початкова фаза коливань?

7. Вивести формули для розрахунку похибок.

Лабораторна робота № 9

Вивчення додавання однаково напрямлених коливань.

І.Вивчення додавання однаково напрямлених коливань рівних частот

Прилади і матеріали : 1) електронний осцилограф СІ-1; 2) два звукових генератори ГЗ-І8; 3) гучномовець 2ГД-19.

Теоретичні відомості та опис приладів

Нехай матеріальна точка бере участь у двох гармонічних коливаннях одного напряму, які відбуваються з однаковою циклічною частотою w, з різними початковими фазами та різними амплітудами:

(1)

. (2)

Для дослідження додавання таких коливань можна скористатись графічним методом зображення гармонічних коливань (рис. 1).

Подамо амплітуди складових коливань радіусами-векторами і . Кожний з цих векторів у початковий момент часу займає положення, яке можна виразити відповідно через кути і (початкові фази). Обидва вектори рухаються проти годинникової стрілки з однаковою кутовою частотою . У кожний момент часу проекції векторів і на вісь Ох можна записати у вигляді рівнянь (1), (2).

Зміщення х тіла від положення рівноваги при участі його одночасно в обох коливаннях виразиться алгебраїчною сумою зміщень (1) і (2), тобто

.

Оскільки сума проекцій двох векторів на деяку вісь дорівнює проекції на ту саму вісь вектора, що є їхньою сумою, то результуюче коливання можна зобразити вектором амплітуди А, знайденим графічним додаванням векторів амплітуд і , тобто

.

З рис. 69 маємо

. (3)

Вектор результуючої амплітуди, очевидно, обертається з тією самою частотою , що й вектори амплітуд складових коливань.

Кут , який утворює вектор результуючої амплітуди з віссю Ох у початковий момент, з OBC визначається так:

.

Результуюче коливання, користуючись графічним способом, можна подати проекцією вектора .

З рис. 69 або . (4)

Як видно з рівняння (4), результуюче коливання є також гармонічним.

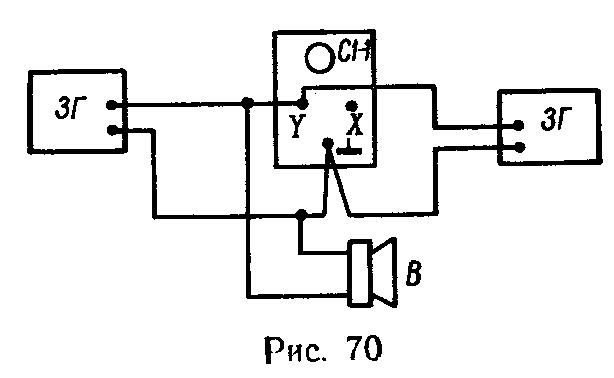
Рис. 1 Рис. 2

Для вивчення додавання двох коливань одного напряму користуються експериментальною установкою, схему якої наведено на рис. 2.

На блок вертикального відхилення електронного осцилографа від двох звукових генераторів (ЗГ) подаються синусоїдні електричні коливання однакової частоти. Значення амплітуди результуючого коливання, як видно з (3), залежить від різниці початкових фаз. Оскільки

, то

.

Результуюче коливання спостерігають на екрані електронного осцилографа.

Порядок виконання роботи

1. Скласти установку за схемою, наведеною на рис. 2.

2. На обох звукових генераторах встановити однакові частоти (частоти задає керівник занять).

3. Ввімкнути живлення одного із звукових генераторів та електронного осцилографа і дати їм прогрітись протягом 2 — 3 хв,

4. Добитись стійкого зображення графіка гармонічного коливання певної частоти на екрані осцилографа.

5. За масштабною сіткою екрана осцилографа визначити амплітуду одержаного гармонічного коливання.

6. Вимкнути перший генератор та ввімкнути другий. По шкалі другого генератора встановити ту саму частоту коливань, яка була на першому генераторі. Одержати на екрані осцилографа графік другого коливання.

7. За масштабною сіткою екрана осцилографа визначити амплітуду другого гармонічного коливання.

8. Одночасно ввімкнути обидва генератори і добитись на екрані осцилографа стійкого зображення графіка результуючого коливання.

9. За допомогою гучномовця В (рис. 70) процес додавання коливань контролювати на слух.

10. За масштабною сіткою екрана осцилографа виміряти амплітуду результуючого коливання.

11. З формули знайти різницю фаз складових коливань, а саме:

.

12. Знаючи різницю фаз та амплітуди , і , побудувати на міліметровому папері векторну діаграму розглядуваних коливань.

? Контрольні запитання

1. Яке коливання дістають від додавання двох однаково напрямлених гармонічних коливань рівних частот?

2. Від чого залежить величина амплітуди результуючого коливання?

3. У чому полягає суть векторного способу додавання коливань?

4. Як визначити початкову фазу результуючого коливання?