ПЕРЕДМОВА

Лабораторний практикум містить опис лабораторних робіт, виконуваних у лабораторії фізики Галицького коледжу імені В’ячеслава Чорновола, а також матеріали необхідні для підготовки до лабораторних робіт, їх виконання та звітності за виконану лабораторну роботу.

При укладанні посібника враховано, що завданням лабораторного практикуму у вищому технічному навчальному закладі, насамперед, є: 1) проілюструвати теоретичні положення і закони фізики; 2) познайомити студентів з вимірювальними приладами, навчити працювати з ними; 3) привити студентам навики виконання експереминтальних досліджень та вміння обробляти результати експерименту. Лабораторний практикум повинен сприяти виробленню вмінь застосовувати теоретичні знання до розгляду конкретних фізичних явищ, бути важливою ланкою у тріаді: теоретичний матеріал – лабораторний практикум – розв’язування задач. Важливість лабораторного практикуму посилюється в останній час у зв’язку з особливостями нових навчальних планів з ряду дисциплін: це змушує розширити традиційні функції лабораторного практикуму, шукати нові форми і методи проведення лабораторних занять.

Особливостями практикуму є те, що: 1) необхідний теоретичний матеріал дається в повному обсязі до кожної лабораторної роботи (з метою забезпечення максимальної зручності при підготовці до виконання даної лабораторної роботи); 2) теоретичний матеріал викладається ,,з прив’язкою” до конкретної лабораторної роботи; 3) вивід робочих формул дається в органічному зв’язку з теоретичним матеріалом.

Робота з електронним курсом у класі може, зокрема, включати демонстрацію інтерактивних моделей.

Курс також може використатися користувачем, що цікавиться фізикою, поза навчальним процесом. Безсумнівно інтерес у цьому випадку можуть викликати ілюстрації посібника і інтерактивні моделі до курсу. Порядок використання курсу в цьому випадку, звичайно, не може бути формалізований.

Мінімальні технічні вимоги до комп'ютера

Операційна система Microsoft Windows 98SE/Me/2000/XP, Internet Explorer 6.0 , процесор Pentium 200 МГц, 200 Mб вільного дискового простору, 64 Mб оперативної пам'яті.

Робота з комп'ютерними моделями

Навчальний курс включає інтерактивні комп'ютерні моделі, які демонструють основні фізичні закони й цікаві фізичні явища. Працюючи з моделями, ви можете провести своє невелике дослідження. Можна міняти значення параметрів або конфігурацію моделі й спостерігати за результатом.

Вибір фізичних параметрів у моделі

Моделі містять інтерфейсні елементи для вибору фізичних параметрів, запуску процесів або зміни станів моделі.

Командні кнопки

Кнопки служать для запуску або зупинки комп'ютерної моделі. Можлива робота як з мишею, так і із клавіатурою.

Вибір чисельних значень параметрів

У комп'ютерних моделях вибір параметрів здійснюється за допомогою спеціальних вікон і кнопок-стрілок для введення й зміни величини параметрів. Натискання на кнопки-стрілки дискретно збільшує або зменшує значення параметра.

Перемикачі

Кнопки перемикання служать для вибору одного із запропонованих варіантів у комп'ютерних моделях.

Вимикачі

Вимикачі в моделях служать для керування налаштуваннями моделі.

Вибір довжини хвилі

Цей спеціалізований елемент керування призначений для вибору довжини електромагнітної хвилі. Можна ввести значення довжини хвилі із клавіатури або, схопивши мишею за скроллер шкали, перетягнути його на потрібні кольори.

Застосування технологій Drag-n-Drop «Схопи й потягни» й Point-n-Click «Вкажи й натисни»

Для зміни положення об'єктів у моделях застосовується технологія «Схопи й Потягни». Якщо над об'єктом моделі курсор змінив свою форму, об'єкт можна перемістити в нове положення з натиснутою мишею.

У деяких моделях можна не перетягувати об'єкт за допомогою курсору, а просто вказати на нове місце розташування курсору й клацнути мишею в зазначеному місці.

Лабораторна робота № 1

Визначення густини речовини тіл правильної геометричної форми.

Прилади і матеріали: мікрометр, штангенциркуль, терези, набір різних тіл правильної геометричної форми.

Теоретичні відомості та опис приладів.

Маса ― це властивість матерії, що характеризує її інертність і гравітацію. Згідно першого закону Ньютона, всі матеріальні тіла мають властивість зберігати стан спокою або рівномірного прямолінійного руху, якщо діючі на них сили взаємозрівноважені. Ця властивість називається інерцією. Скалярна величина, що характеризує інерцію тіла, називається його інертною масою. Чим повільніше тіло змінює свій стан під дією сили, тим більша його маса. З визначення зрозуміло, що маса будь-якого тіла більша від нуля. Маса — величина адитивна. Вона не залежить ні від умов, в яких перебуває тіло, ні від взаємодії його з іншими тілами.

Маса фігурує у двох різних законах: у другому законі Ньютона і в законі всесвітнього тяжіння. В першому випадку вона характеризує інертні властивості тіла, у другому — гравітаційні властивості, тобто властивість тіл притягуватися одне до одного. Ньютон вважав, що ці дві фізичні характеристики тіла збігаються, тому він користувався одним терміном — "кількість матерії", що рівнозначний тепер слову "маса". Справедливість твердження про рівність інертної і гравітаційної мас випливає з того, що прискорення вільного падіння в даній точці Землі для різних тіл є сталим.

Маса — одна з основних характеристик тіла; вона залежить від розмірів тіла і від природи речовини, з якої складається тіло.

Величина маси може бути визначена по різних її проявах: інерції, тяжіння — шляхом порівнювання з масою еталонного тіла, вибраною за одиницю.

Вага тіла — це сила, з якою нерухоме відносно Землі тіло діє на горизонтальну опору або вертикальний підвіс. Вагу тіла можна представити як рівнодійну двох сил, які діють на тіло: сили тяжіння, яка направлена до центру Землі та відцентрової сили інерції, що обумовлена обертанням Землі навколо головної осі.

Якщо знехтувати впливом добового обертання Землі, то згідно закону всесвітнього тяжіння, сила тяжіння, тобто вага тіла біля поверхні Землі визначається за формулою:

де: G — гравітаційна стала, m — маса тіла, М_з — маса Землі, R — віддаль від тіла до центра Землі, яка дорівнює радіусу Землі (R = 6 378 164 м).

Дослід показує, що сила тяжіння, що діє на дане тіло в різних точках Землі, дещо відрізняється — вона змінюється в залежності від географічної широти та від висоти над рівнем моря; таким же чином змінюється і прискорення вільного падіння. Але для будь-якого тіла відношення сили тяжіння до прискорення вільного падіння є величина стала:

Отже, відношення діючої на тіло сили тяжіння до прискорення вільного падіння є деякою характеристикою даного тіла і ця величина називається масою тіла: .

Густиною речовини називається фізична величина, яка вимірюється відношенням маси тіла до його об'єму:

. (1)

Фізичний зміст густини: це фізична величина, яка чисельно дорівнює масі тіла в одиниці об'єму. Формула (1) справедлива лише для однорідних тіл. В неоднорідних тілах густина різних ділянок різна. В цьому випадку вибирають малий об'єм dV, всередині якого тіло можна рахувати однорідним.

Перейшовши до границі при 0 одержуємо формулу густини у випадку неоднорідного тіла

.

Одиниці вимірювання густини: г/см³, кг/м³.

Питомою вагою тіла називається фізична величина, яка вимірюється відношенням ваги тіла у вакуумі до його об'єму.

. (2)

У випадку неоднорідних тіл

.

Одиниці вимірювання питомої ваги: дин/см³, Н/м³.

Співвідношення між питомою вагою і густиною таке ж, як між вагою і масою, тобто:

D =g

В зв'язку з тим, що питома вага залежить від географічної широти місця, від висоти над рівнем моря, в практиці користуються густиною, а не питомою вагою. Як видно з формул (1) і (2), для визначення густини  і питомої ваги D необхідно знати масу тіла m, вагу тіла Р і його об'єм V. Об'єм тіл правильної геометричної форми може бути легко обчислений за відповідними

математичними формулами, а густина цих тіл ― знайдена за формулою (1).

Наприклад:

1. Паралелепіпед. Його об'єм V=abc, де a, b, c — довжини його ребер, тоді густина дорівнює:

.

2. Циліндр. Його об'єм , де d — діаметр основи, h — висота циліндра, тоді густина дорівнює:

.

3. Куля. Її об'єм , де d — діаметр, тоді густина дорівнює:

.

4. Циліндричне кільце. Його об'єм і густина відповідно дорівнюють:

,

,

де d_зов ― зовнішній діаметр, d_вн — внутрішній діаметр, h — висота.

Необхідні для обчислення лінійні розміри тіл (висота, діаметр, довжина) можуть бути визначені шляхом безпосередніх вимірювань за допомогою мікрометра або штангенциркуля, а маса — на терезах.

ОПИС ПРИЛАДІВ

Терези.

В даній роботі масу визначаємо за допомогою важільних терезів.

Важільні терези складаються з коромисла 1; яке являє собою прямолінійний рівноплечий важіль. Ребро стальної призми, вмонтованої посередині коромисла, спирається на агатову пластинку, що лежить зверху колонки 7 терезів, встановленої на станині 4.На кінцях коромисла є також стальні призми, на які за допомогою сережок 2 підвішуються шальки 3 терезів. До середини коромисла, перпендикулярно до лінії, що сполучає крайні призми, прикріплено довгу стрілку 6, за якою визначається положення коромисла. При коливанні коромисла кінець цієї стрілки переміщується вздовж шкали, яка закріплена на основі колонки. Шкала посередині має поділку 10, крайня ліва позначається 0, крайня права — 20. Тобто, шкала має 20 поділок. Щоб оберегти призму від затуплення, а терези від псування, внизу колонки є спеціальний пристрій — аретир 5, яким піднімають коромисло та шальки терезів, коли терезами не користуються.

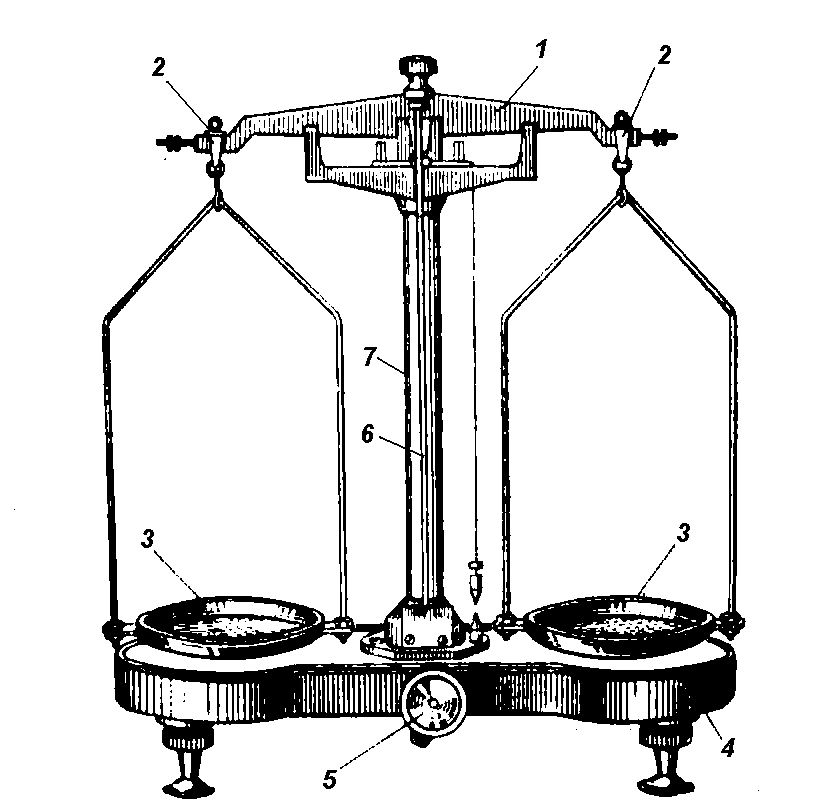
На технічних терезах можна зважувати з точністю до 0,01г. До терезів додаються у футлярі важки від 100г до 1г та від 10мг до 500мг.

Правила користування технічними терезами:

1. Відпустити аретир і перевірити справність терезів.

2. Якщо терези не аретировані, не можна класти на шальки терезів або знімати з них зважуване тіло і важки.

3. Зважуване тіло класти на ліву шальку, а важки — на праву.

4. Важки вибирати тільки пинцетом.

5. Закінчивши зважування, терези треба аретирувати, важки зняти з шальок і покласти у відповідні гнізда футляра.

Штангенциркуль.

Даний прилад складається із стальної лінійки (штанги) 5 з міліметровими поділками, відносно якої переміщується рамка 4 з ноніусом, і двох пар губок (ніжок) ― нерухомих 1 і рухомих 2. При зімкнутих губках відлік за ноніусом дорівнює нулю. Між губками затискують вимірювану деталь. Щоб точно визначити розмір деталі, рухому губку штангенциркуля переміщують у момент дотику її до деталі за допомогою мікрометричного пристрою 6, щоб запобігти надмірному натисканню губок на деталь. Закріплюють рухому губку на штанзі стопорним гвинтом 3 (при відповідних навичках роботи з штангенциркулем гвинт 3 можна не закріпляти) і роблять відлік за ноніусом. Для вимірювання внутрішніх розмірів деталі є калібровані губки 7. Загальна ширина їх при зведених губках найчастіше дорівнює 10мм; цей розмір треба додавати до відліку за шкалою. Деякі штангенциркулі мають також висувні лінійки для вимірювання глибини ненаскрізних отворів.

М ікрометр.

Мікрометр складається із стальної скоби 8, що має нерухому опорну п’яту 1, стебла 3, мікрометричного гвинта 2 і стопорного гвинта 7.

Мікрометричний гвинт переміщується всередині спеціальної гільзи з різьбою, закріпленою в стеблі 3. Крок гвинта 0,5 ― 1,0 мм. На зовнішній поверхні стебла нанесено дві поздовжні шкали, зсунуті одна відносно другої на 0,5 мм. Зовні стебло охоплює барабан 4, з’єднаний з мікрометричним гвинтом. Таким чином, при обертанні барабана обертається і гвинт; при цьому переміщується його вимірювальна поверхня 2. Дія мікрометра грунтується на властивості гвинта здійснювати при повороті його поступальне переміщення, пропорційне куту повороту. Скошений обід 6 барабана поділено на 50 (або на 100) однакових поділок. На правому кінці барабана є особливий фрикційний пристрій ― тріскачка 5. При вимірюванні слід обертати барабан тільки за головку тріскачки. Деталь при вимірюванні затискається між п’ятою і мікрометричним гвинтом. Після того, як досягнуто певного ступеня натиску на деталь (5 ― 6 Н), фрикційна головка починає проковзувати, даючи характерний тріск. Завдяки цьому затиснута деталь деформується порівняно мало (її розміри не спотворюються) і, крім того, це запобігає псуванню мікрометричного гвинта.

Для відлічування показів мікрометра по шкалі стебла визначають ціле число (нижня шкала) і половини (верхня шкала) міліметрів. Для відлічування сотих часток міліметра користуються поділками на барабані (крок мікрометричного гвинта визначається заздалегідь).

Примітка. Якщо при вимірюванні над поздовжньою лінією стержня (тобто на верхній лінійній шкалі) після відрахованого числа цілих міліметрів виступає ще одна поділка, то до одержаного результату необхідно додати ще 0,5мм.

Порядок виконання роботи.

1. Зважити кожне тіло на технічних терезах.

2. Виміряти лінійні розміри тіл, які необхідні для визначення об'ємів.

3. Результати вимірювання занести в таблиці. Кожне вимірювання провести тричі для кожного тіла і для кожної величини знайти середнє значення. Підставляючи у відповідні формули отримані дані, знаходимо густину речовини тіл правильної геометричної форми.

4. Обчислити середнє значення густини тіла, визначити похибки і записати кінцевий результат у вигляді:

=_{сер± }_сер

= (_сер /_сер)100%

Таблиця 1. Паралелепіпед.

№	а,	в,	с,	m,	,	,
1.
2.
3.
Сер.

= =

Таблиця 2. Циліндр.

№	d,	h,	m,	,	,
1.
2.
3.
Сер.

= =

Таблиця 3. Циліндричне кільце.

№	dзовн	dвнтр	h,	m,	,	,
1.
2.
3.
Сер.

= =

Таблиця 4. Куля.

№	D	M,	,	,
1.
2.
3.
Сер.

= =

5. Зробити висновок.

? Контрольні запитання і завдання

1. Який фізичний зміст маси та ваги тіла?

2. Що називається густиною речовини? Що називається питомою вагою? Одиниці вимірювання густини і питомої ваги? Яке співвідношення між питомою вагою і густиною?

3. Будова технічних терезів і правила користування?

4. Будова, принцип дії та правила користування штангенциркулем. Охарактеризувати ноніус. Виконати вимірювання.

5. Будова та призначення окремих частин мікрометра. Правила користування мікрометром.

6. Вивести робочі формули для визначення густини речовини тіл правильної геометричної форми. Як за робочою формулою знайти вираз для обчислення відносної похибки?

7. Виконати вимірювання розмірів запропонованого тіла мікрометром. Записати результати вимірювання.

8. Шлакоблочний завод виготовив для шляхового будівництва залізобетонні плити розміром 1,21,21,5 м. Кожна з них важить 0,5 т. Визначити, який процент у плитах становить залізна арматура.

Лабораторна робота № 2

Вивчення руху тіл по похилій площині під дією власної ваги

Прилади і матеріали: похила площина, досліджувані тіла (дерев’яні бруски), масштабна лінійка, секундомір.

Теоретичні відомості та опис приладів.

На тіло масою m (рис.1) , що перебуває на похилій площині АВ, діє сила тяжіння і сила тертя . Складова сили тяжіння (її називають скочуючою)

F_ск =mg sin  (1)

діє вздовж площини донизу. Силою тертя називається сила:

F_T=kN=kmg cos  (2)

де N=mg cos   сила нормального тиску тіла на площину, k – коефіцієнт тертя. Сила тертя перешкоджає рухові тіла в напрямі F_ск.

При малих кутах підйому площини  переважає сила тертя F_T і тіло залишається у спокої; при великих кутах  переважає сила F_ск і тіло рухається. При певному проміжному куті підйому с, який називається кутом тертя спокою, сили F_T і F_ск зрівнюються, тобто

mg sin _с = k mg cos _с.

Тоді tg _с=k. (3)

Тіло ще утримується в спокої на площині, але в цьому випадку кут _с  найбільший з можливих кутів спокою; навіть незначне його збільшення зумовить рух тіла з прискореням, яке обчислюється за другим законом Ньютона:

a= (F_ск-F_Т)/m=g(sin -k cos ). (4)

Проаналізуємо цю формулу. Коли коефіцієнт тертя k і кут підйому  залишаються під час руху незмінними, то незмінним буде прискорення а, тобто рух тіла по похилій площині буде рівноприскореним. Найменшим з можливих прискорень при цьому буде а=0, а найбільшим  а=g. З формули (4) випливає, що а=0 при умові

sin  - k cos =0,

тобто tg = k.

Коли sin-kcos=1 (тобто =/2), то a=g. При а=0 отримуємо рівномірний рух, при а=g – вільне падіння тіл.

Таким чином, якщо немає сторонніх впливів, то тіло на похилій площині залишатиметься непорушним при всіх кутах підйому, не більших від кута тертя спокою arctg k_с . Коли =arctg k, то тіло, зрушене з стану спокою, рухатиметься рівномірно. Коли ж кут підйому >arctg k, то тіло рухатиметься з прискоренням, яке задовіольнятиме нерівність: 0  a  g.

Якщо на тіло діє стороння сила (для визначеності спрямуємо її вздовж похилої площини донизу), то тіло набуде прискорення а, яке визначається з другого закону Ньютона:

a=(F_ск+F-F_Т)/m= F /m+g(sin -k cos ). (6)

В залежності від кута підйому площини, коефіцієнта тертя і зовнішньої сили F прискорення може набувати значень у межах від 0 (при F_ск+F= F_Т) до . Формула (6) охоплює, власне кажучи, і випадок F<0 (напрям уздовж похилої площини вгору). При цьому знак сили F_Т визначається знаком меншої з |F_ск| i |F|.

Коефіцієнт корисної дії  похилої площини визначається відношенням корисно витраченої роботи А_к до затраченої А_з:

=А_к/А_з.

При переміщенні тіла по похилій площині під дієї власної ваги від точки В до точки А (відстань між ними АВ=l) корисна робота обчислюється таким чином:

А_к= mal=mg(sin -k cos )h/sin .

Затрачена робота: А_з=F_скl=mgh.

Звідси

=mgh(sin -k cos )/mgh sin =1-k ctg , (7)

тобто  залежить від коефіцієнта тертя k і кута підйому площини .

П роаналізуємо знайдену нерівність. Оскільки k i ctg  (в першому квадранті) додатні, то  повинна бути менша за одиницю: 1. Це твердження узгоджується із законом збереження енергії для будь-якого механізму. Якщо в реальних умовах при наявності тертя (k0) кут підйому  поступово зменшувати, то ККД також повинен зменшуватися і при ctg =1/k (або tg =k) досягне нуля. Нульовому значенню ККД відповідає випадок, коли скочуюча сила ледве зрівноважує силу тертя і тіло рухається за інерцією, не потребуючи енергії. При дальшому зменшенні кута підйому ККД стане від’ємним (<0) через недостатню власну вагу для забезпечення руху і потребує дії зовнішніх сил.

Порядок виконання роботи.

1. Поклавши досліджуване тіло на похилу площину, виміряти її довжину l.

2. Повільно збільшувати кут підйому площини, злегка постукуючи по ній або підштовхуючи тіло, поки воно не почне рівномірно сковзати вниз, записати висоту підйому площини ВС=h.

3. Дослід провести три рази.

4. Обчислити середнє значення висоти підйому ₀ і за формулою (5) знайти коефіцієнт тертя k.

5. Встановити похилу площину під довільним кутом >_c і за допомогою секундоміра виміряти час зісковзування тіла з площини.

6. Повторити дослід, описаний в п.5 ще два рази . Знайти t_c.

7. За формулою

a_с=2L/t_с² (8)

обчислити середнє прискорення тіла під час руху по похилій площині.

8. Обчислити прискорення а за теоретично доведеною формулою (4), використавши знайдене в п.4 значення коефіцієнта тертя k.

9. Знайти абсолютну та відносну похибки отриманого прискорення.

10. За формулою (7) обчислити ККД похилої площини.

11. Повторити описані досліди для іншого досліджуваного тіла.

12. Результати записати в таблицю.

№пп

H

hc

l

0

k



t

tc

ac

a

a

E,%



1

1т.

2

3

1

2т.

2

3

13. Зробити висновок.

? Контрольні запитання і завдання

1. Закони Ньютона.

2. Імпульс, закон збереження імпульсу. Енергія, закон збереження енергії.

3. У шкільному досліді з мертвою петлею кульку масою m

відпустили з висоти h=3R (де R-радіус петлі). З якою силою тисне кулька в нижній і верхній точках петлі?

Лабораторна робота № 3

Вивчення руху тіла кинутого горизонтально.

Прилади і матеріали: комп’ютерна модель рух тіла, кинутого під кутом до горизонту.

Теоретичні відомості та опис приладів.

Розглянемо два випадки складного руху: рух тіла кинутого горизонтально і рух тіла, кинутого під кутом до горизонту.

а) Рух тіла, кинутого горизонтально.

Припустимо, що матеріальній точці, яка знаходиться на деякій висоті над вибраною поверхнею, в момент часу t=0 надано початкової швидкості у горизонтальному напрямку. Тоді точка братиме участь у двох рухах (рис.1).

По-перше, вона рухатиметься горизонтально із сталою швидкістю (в горизонтальному напрямку не діють ніякі сили), проходячи протягом послідовних одиничних проміжків часу однакові відстані ОХ₁, X₁X₂, X₂X₃ і т.д.

По-друге, вона рухатиметься по вертикалі під дією сили тяжіння з прискоренням , проходячи відповідно за одну секунду шлях ОY₁, за дві секунди - ОY₂, за три секунди - ОY₃ і т.д. Причому ОY₁ : ОY₂ : ОY₃ : ... = 1² : 2² : 3² : ...

Оскільки матеріальна точка М бере одночасно участь в обох рухах, то вона пройде через точки Р₁, Р₂, Р₃, .... Шлях пройдений у горизонтальному напрямі визначається рівнянням

x=₀t. (1)

Рівняння другого руху (вертикального) буде:

у=gt²/2 (2)

Виключаючи t з (1) і (2) одержимо рівняння траєкторії:

(3)

Це є рівняння параболи. Отже, тіло, кинуте горизонтально, рухається по параболі, вершина якої лежить у точці кидання.

Час польоту тіла можна визначити із законів вільного падіння: у=gt²/2.

Звідси t= ,

Оскільки y=h, то t= .

Дальність польоту визначається за формулами:

S_x=₀t, або S_x= (4)

Кутове відхилення тіла від напряму кидання можна знайти із співвідношення (рис.1)

(5)

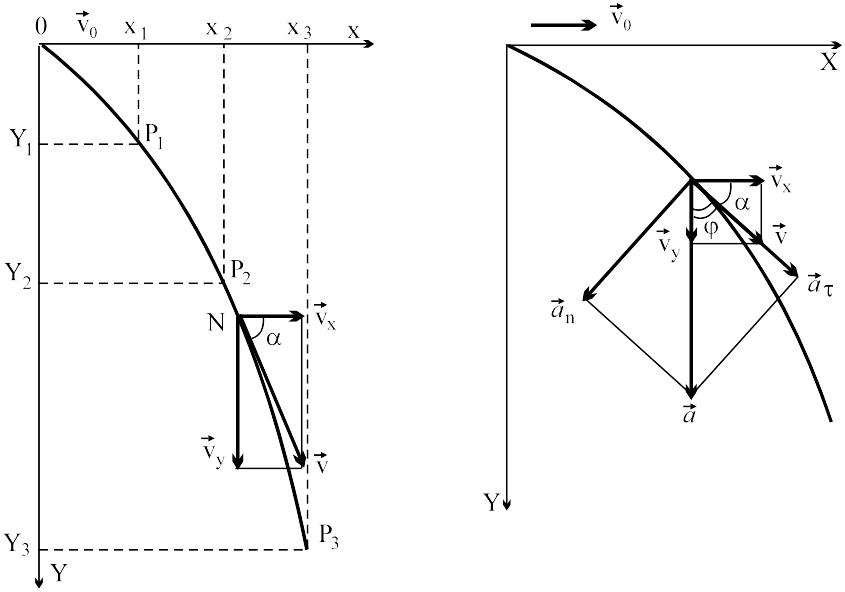
Рис.1 . Рис.2.

Як видно з рис.2 швидкість руху тіла в деякий момент часу напрямлена по дотичній до траєкторії і дорівнює , де — горизонтальна складова швидкості, — вертикальна складова.

Якщо вертикальна складова дорівнює , а горизонтальна , то _.

Через те, що горизонтальна складова швидкості тіла весь час залишається сталою, то горизонтальна складова прискорення дорівнює нулю.

Тому повне прискорення тіла весь час дорівнює прискоренню сили тяжіння . Повне прискорення тіла можна розкласти на дві складові (див. рис.2). Перша називається дотичною або тангенціальною ( ) складовою, друга – нормальною ( ). Тангенціальне прискорення характеризує тільки зміну числового значення швидкості з часом, тому визначається за формулою

.

Тангенціальне прискорення напрямлене по дотичній до траєкторії руху і в напрямку швидкості або проти неї, залежно від того, збільшується чи зменшується величина швидкості.

Нормальне або доцентрове прискорення визначає зміну швидкості за напрямком і воно перпендикулярне до вектора швидкості.

Знаючи a_t і a_n, можна знайти модуль і напрям повного прискорення (рис.2) , , де j=90°–a.

б) Рух тіла кинутого під кутом до горизонту.

Тепер розглянемо рух матеріальної точки, кинутої під кутом a до горизонту (рис.3) з початковою швидкістю v_o. Для його опису зв’яжемо систему відліку з Землею і спрямуємо вісь ОХ горизонтально, а вісь OY —вертикально. Рисунок доповнятимемо поступово.

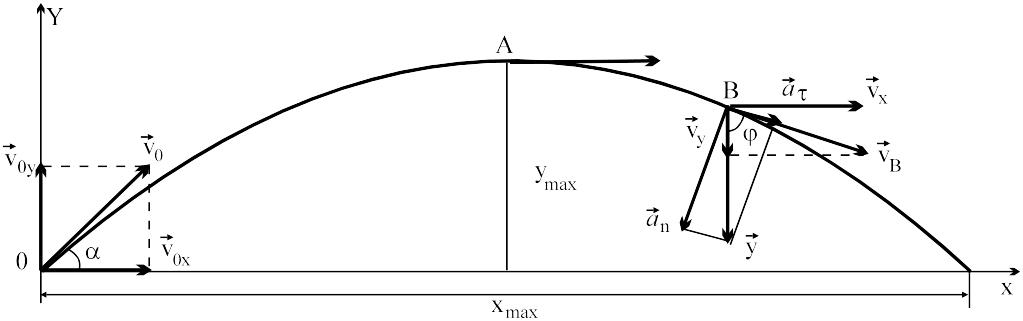
Рис.3.

1) по осі ОХ рух рівномірний, так як в горизонтальному напрямі на тіло ніякі сили не діють.

Залежність координати x від часу визначається так:

x= ₀ t cosa (6)

2) по осі OY рух рівно змінний з сталим прискоренням g=9,8м/c² напрямленим проти осі OY, так як на тіло діє стала сила . Залежність координати у від часу для цього руху така:

(7)

Вирази (6) і (7) – визначають закон руху матеріальної точки кинутої під кутом до горизонту. Виключаючи t з цих виразів одержимо рівняння траєкторії руху:

(8)

Це рівняння параболи, вітки якої напрямленні вниз, а вершина зміщена відносно початку координат. Дальність польоту можна обчислити за формулою: (9)

З рівняння бачимо, що дальність польоту найбільша при a=45°. Найбільшу висоту підняття тіла знайдемо з рівняння (7). Підставляючи в нього , oдержимо (10)

Для визначення нормального і тангенціального прискорення в довільній точці траєкторії розглянемо точки А і В (рис.3). В найвищій точці траєкторії А проекція швидкості на вісь OY дорівнює нулю, а на вісь ОХ – ₀=const. Отже, в точці А тангенціальне прискорення тіла дорівнює нулю, нормальне прискорення a_n=g. В точці В (точка знаходиться за вершиною) розкладемо вектор швидкості на і . Повне прискорення тіла в цій точці дорівнює g. Розкладемо його на і . З рис.3 випливає, що і , де j—кут між і , причому ;

.

Уважно розглянете малюнок, знайдіть всі регулятори й інші основні елементи. Модель демонструє рух тіла, кинутого під кутом до горизонту. Можна змінювати початкову висоту y, а також модуль і напрям швидкості тіла, кут α. У режимі "Стробоскоп" на траєкторії через рівні проміжки часу показуються вектор швидкості кинутого тіла і його проекції на горизонтальну і вертикальну осі.

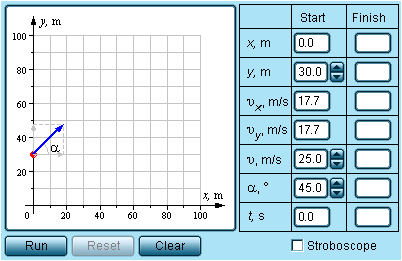
Замалюйте поле експерименту й траєкторію руху частки. Нажавши кнопку "Run", спостерігайте на екрані рух тіла.

Одержіть у викладача допуск для виконання вимірів.

Порядок виконання роботи.

1. Встановіть початкову швидкість у горизонтальному напрямку ( =0). Провівши кидання, з висоти вилітання кульки Y і визначіть дальність кожного польоту Х.

2. Дані записати в таблицю.

3. Аналогічні досліди провести для різних висот Y₂, Y₃, Y₄, Y₅, вимірюючи при цьому відповідні дальності польоту кульки X₁ ... X_5. Результати вимірювань записати в таблицю.

4. Перевірити правильність співвідношень:

а) час польоту кульки за фармулою ;

б) рівняння траєкторії

5. За отриманими даними перевірити співвідношення:

X₁ : X₂ : X₃ : X₄ : X₅ = t₁ : t₂ : t₃ : t₄ : t₅

6. В масштабі побудувати траєкторію руху кульки при різних Y.

   № пп	Y, м	X,м	t,	0,
   1.
   2.
   3.
   4.
   5.

7. Зробити висновок.

? Контрольні запитання і завдання

1. Основні поняття кінематики: основна задача механіки, система відліку, поступальний рух.

2. Швидкість, прискорення і переміщення при рівноприскореному русі.

3. Рух тіла по кривій.

4. Порядок виконання роботи.

5. М`яч кинуто горизонтально з швидкістю 9,8 м/с. Через скільки часу і в якому місці нормальне прискорення буде вдвічі більше за тангенціальне?

Лабораторна робота №4

Вивчення законів кінематики і динаміки поступального руху на машині Атвуда

Мета : Вивчити другий закон Ньютона на прикладі руху двох тіл, зв'язаних невагомою нерозтяжною ниткою, перекинутою через легкий блок..

Основні теоретичні відомості

Машина Атвуда дає змогу одержати рівномірний та рівномірно прискорений рухи тягарців, а також виміряти проміжки часу, протягом яких тягарці проходять задані відстані в рівномірному та рівно-прискореному рухах.

Машина Атвуда складається з вертикального стояка , на верхньому кінці якого закріплено легкий блок, що обертається з малим тертям навколо горизонтальної осі. Через блок перекинуто тоненьку нитку з прикріпленими до її кінців вантажами однакової маси m (маса їх відома, її повідомляє лаборант).

Розглянемо рух системи, що складається з пробних тіл (вантажів), маса кожного з яких m, і блока радіуса r з моментом інерції I. Нехай на правий вантаж покладено тягарець масою Δm. Тоді система тіл масою 2m + Δm пройде відстань s.

За законом збереження енергії

= (1)

Коли нитка не ковзає по блоку, швидкість v руху нитки (швидкість руху системи тіл масою 2m + Δm) дорівнює лінійній швидкості точок обода блока r, тобто

, (2)

a

. (3)

Нехтуючи силою тертя F і моментом інерції блока, при умові, що з (1), (3) для прискорення системи маємо

. (4)

Звідси видно, що система рухатиметься з прискоренням меншим, ніж прискорення вільного падіння. Збільшуючи масу додаткового тягарця, можна збільшити і прискорення системи. Відстані s, яку проходить система тіл однакова для вантажів праворуч і ліворуч та одина і таж для всіх дослідів.