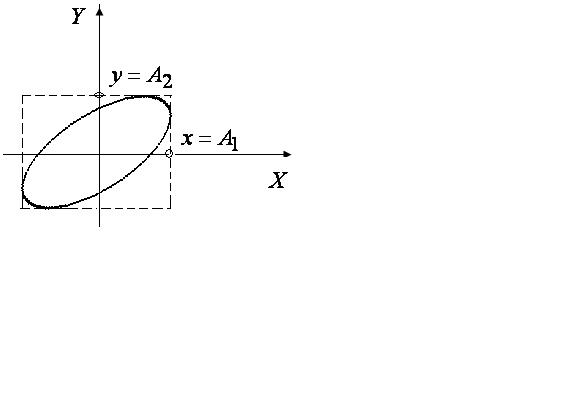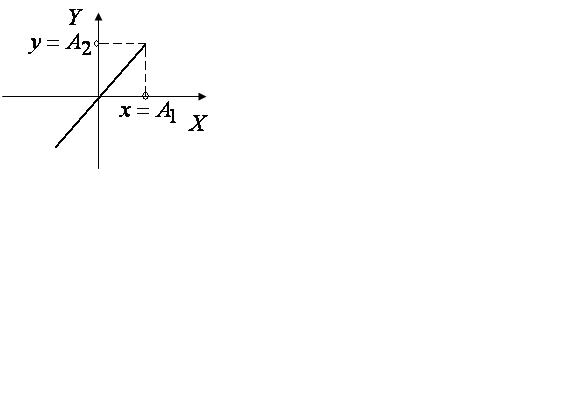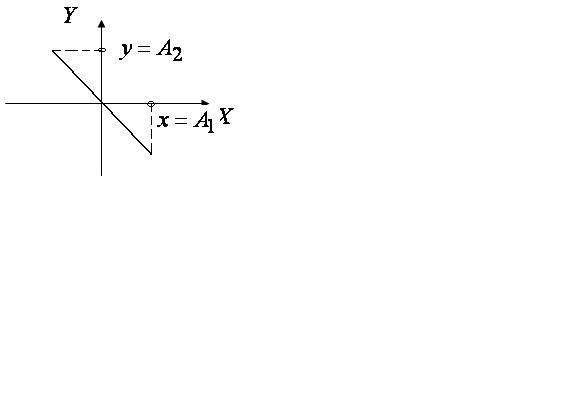- •Тема 1. Введение Материя и формы ее движения. Значение физики в медицине.
- •Классификация медицинской электронной аппаратуры
- •Классификация медицинской электроники по функциональному назначению:
- •II. Классификация медицинской аппаратуры по принципу действия.
- •Действие электрического тока на организм.
- •Обеспечение электробезопасности при работе с медицинской аппаратурой.
- •Основные требования электробезопасности
- •Классификация медицинской аппаратуры по способу дополнительной защиты от поражающего действия электрического тока.
- •Надежность медицинской аппаратуры
- •Тема 2. Механические колебания
- •Основные определения и характеристики колебательного процесса.
- •Дифференциальное уравнение, решение. График.
- •Полная энергия колеблющейся точки.
- •Затухающие колебания. Дифференциальное уравнение, его решение. График. Логарифмический декремент затухания.
- •Вынужденные колебания. Дифференциальное уравнение. Решение. Резонанс.
- •Автоколебания.
- •Сложение гармонических колебаний, направленных вдоль одной прямой.
- •Сложение взаимно перпендикулярных колебаний.
- •Сложное колебание. Гармонический спектр сложного колебания. Теорема Фурье.
- •Тема 3 механические волны.
- •Уравнение плоской механической волны.
- •Энергия волны. Поток энергии волны. Вектор Умова.
- •Эффект Доплера.
- •Тема 4. Акустика. Природа звука.
- •Физические характеристики звука.
- •Характеристики слухового ощущения (Физиологические характеристики).
- •Шкала уровней громкости.
- •Звуковые методы исследования в клинике.
- •Тема 5. Гидродинамика
- •Уравнение неразрывности струи
- •Уравнение Бернулли
- •Практические следствия из уравнения Бернулли.
- •Вязкость жидкости.
- •Ламинарное и турбулентное течение
- •Распределение скорости и градиента по сечению трубы при ламинарном течении.
- •Течение реальной жидкости по горизонтальной трубе постоянного сечения. Закон Гагена - Пуазейля.
- •Течение жидкости по горизонтальной трубе переменного сечения
- •Течение жидкости по разветвленной трубе
- •Течение жидкости по трубе с эластичными стенками
- •Тема 6. Биореология.
- •Зависимость коэффициента вязкости крови
- •Физические модели кровообращения.
- •Закономерности выброса и распространения крови в большом круге кровообращения.
- •Работа и мощность сердца.
- •Тема 7. Биологические мембраны Значение и функции биологических мембран. Строение мембран.
- •Физиологические функции мембран.
- •Физические свойства мембран.
- •Модели искусственных мембран для изучения свойств мембран.
- •Методы исследования мембран
- •1. Микрокалориметрия.
- •3. Люминесцентный анализ.
- •4. Рентгеноструктурный анализ.
- •5.Электронный парамагнитный резонанс (эпр).
- •6.Ядерный магнитный резонанс (ямр)
- •Диффузия в жидкостях. Закон Фика.
- •Пассивный транспорт веществ.
- •Перенос незаряженных частиц (атомов и молекул) через мембрану
- •Перенос заряженных частиц (ионов) через мембрану.
- •3. Облегченная диффузия.
- •Активный транспорт.
- •Тема 8. Электромагнитные явления в биологических системах.
- •Равенство Доннана.
- •Потенциал покоя
- •Потенциал действия.
- •Распространение потенциала действия. (проведение возбуждения по нервным волокнам).
- •Тема 9. Биофизические принципы исследования электрических полей в организме.
- •2. Электрический дипольный момент диполя
- •Напряженность электрического поля диполя.
- •Потенциал. Разность потенциалов.
- •Диполь в электрическом поле.
- •Токовый диполь. Эквивалентный электрический генератор.
- •Тема 10. Электрокардиография
- •Метод отведений Эйнтховена
- •Блок-схема кардиографа.
- •Вектор-электрокардиография.
- •Тема 11. Электродинамика Электрические колебания.
- •Колебательном контуре.
- •Незатухающие электромагнитные колебания.
- •Затухающие колебания
- •Вынужденные колебания.
- •Тема 12. Импульсные токи Апериодический разряд конденсатора
- •Характеристики импульсных токов.
- •6. Коэффициент заполнения
- •Генераторы импульсных токов.
- •Изменение формы импульса.
- •Дифференцирующая цепь
- •Интегрирующая цепь.
- •Действие импульсного тока на ткани организма
- •Тема 13.
- •Биологические основы реографии
- •Цепи переменного тока, содержащие отдельные элементы
- •Цпт, содержащая последовательно включенные активное, индуктивное и ёмкостное сопротивления
- •Цепь переменного тока, содержащая параллельно включенные активное, индуктивное и ёмкостное сопротивления
- •Тема 14. Электромагнитное поле. Электромагнитные волны
- •Основные положения электромагнитной теории Максвелла.
- •Уравнение электромагнитной волны.
- •Энергия электромагнитной волны
- •Шкала электромагнитных волн.
- •Физические процессы, происходящие в тканях организма под действием токов и электромагнитного поля
- •3. Переменное магнитное поле.
- •Тема 15. Поляризация света
- •Методы получения полностью поляризованного света
- •При отражении от неметаллического зеркала
- •2.При двойном лучепреломлении
- •3. Дихроизм.
- •Система поляризатор – анализатор
- •Вращение плоскости поляризации. Поляриметрия.
- •Поляризационный микроскоп
- •Тема 16. Тепловое излучение. Природа теплового излучения.
- •Характеристики теплового излучения
- •Закон Кирхгофа
- •Спектр излучения ачт
- •Законы излучения абсолютно черного тела
- •Формула Планка и её применение для уточнения законов теплового излучения абсолютно черного тела
- •Тема 17 элементы квантовой физики Волновые свойства частиц. Длина волны де Бройля
- •Электронный микроскоп
- •Люминесценция
- •В зависимости от причины, вызвавшей свечение:
- •Фотолюминесценция
- •Закон Стокса
- •Применение люминесценции в медицине
- •Индуцированное излучение Лазеры – оптические квантовые генераторы
- •Свойства лазерного излучения
- •Применение лазеров в медицине
- •Голография и возможности её применения в медицине
- •Тема 18. Рентгеновское излучение
- •Свойства рентгеновского излучения
- •Механизмы генерации рентгеновского излучения
- •Рентгеновская трубка
- •Зависимость энергии рентгеновского излучения от рабочих параметров рентгеновской трубки.
- •Действие рентгеновского излучения на вещество
- •Применение рентгеновского излучения в медицине
- •Тема 19. Ионизирующее излучение
- •Строение атомного ядра
- •Модели строения ядра
- •Энергия связи
- •Радиоактивность. Виды излучений
- •Основной закон радиоактивного распада
- •Радиоактивность в природе – естественная фоновая радиация
- •Дозиметрия ионизирующего излучения Проникающая и ионизирующая способности радиоактивного излучения
- •Биофизические основы действия ионизирующего излучения на организм
- •Характеристики ионизирующего излучения
- •Дозиметрическая аппаратура
- •Защита от ионизирующего излучения
Сложение гармонических колебаний, направленных вдоль одной прямой.
Смещение тела, участвующего одновременно в двух или нескольких колебаниях, находится на основании принципа суперпозиции, согласно которому эти колебания накладываются, не влияя одно на другое.
Пусть материальная точка участвует в двух гармонических колебаниях, направленных вдоль одной прямой, круговые частоты этих колебаний одинаковы, а начальные фазы различны. Такие колебания описываются уравнениями:
![]()
![]()
При сложении колебаний направленных по одной прямой результирующее смещение точки в любой момент времени равно сумме смещений, которые точка имела бы в каждом из колебаний в отдельности в тот же момент времени:
![]()
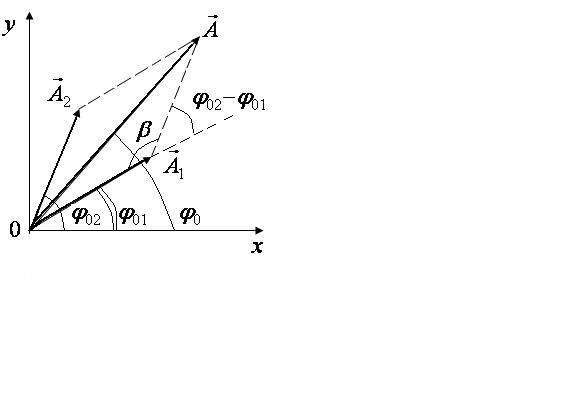
Такое сложение значительно облегчается, если использовать метод векторной диаграммы. Векторной диаграммой называется графическое изображение колебаний в виде векторов на плоскости (рис. 2.4.).
Рис. 2.4. |
![]()
Амплитуда результирующего колебания
![]()
Частные случаи:
1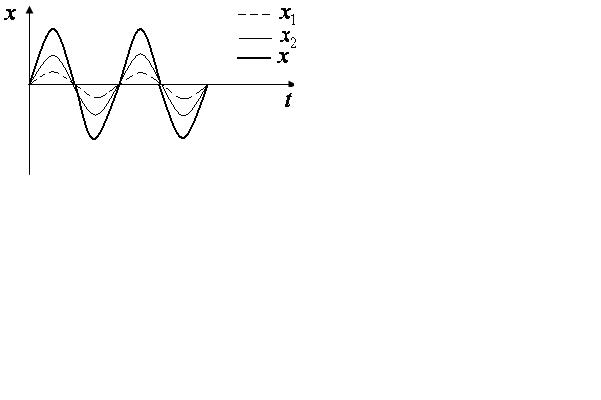 )
если
)
если
![]() ,
где
,
где
![]() ,
то амплитуда результирующего колебания
равна
,
то амплитуда результирующего колебания
равна
![]()
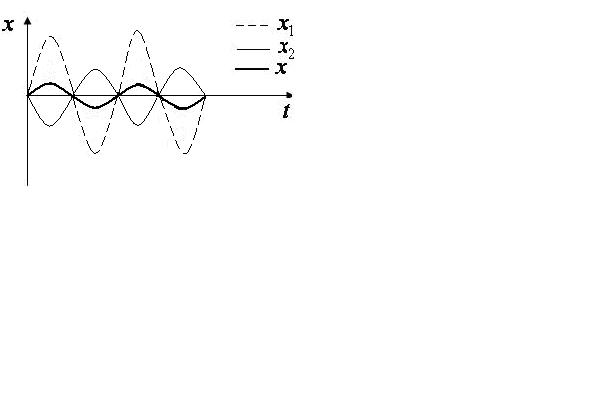
2)
если
![]() где
,
то амплитуда результирующего колебания
равна
где
,
то амплитуда результирующего колебания
равна
![]()
Сложение взаимно перпендикулярных колебаний.
Допустим, что материальная точка может совершать колебания как вдоль оси Ох, так и вдоль оси Оy с одинаковой круговой частотой 0. Тогда уравнения колебаний запишутся следующим образом:
Рис. 2.5. |
![]()
Если возбудить оба колебания, то материальная точка будет двигаться по некоторой криволинейной траектории, форма которой зависит от разности фаз колебаний.
если
 ,
то материальная точка движется по
траектории, заданной уравнением эллипса:
,
то материальная точка движется по
траектории, заданной уравнением эллипса:
![]()
Если
![]() ,
где
,
где
![]() ,
то
,
то
![]() и материальная точка совершает
колебания вдоль этой прямой (рис. 2.6,
рис. 2.7)
и материальная точка совершает
колебания вдоль этой прямой (рис. 2.6,
рис. 2.7)
|
|
Рис. 2.6 |
Рис. 2.7 |
Если
![]() ,
то материальная
точка движется по траектории, заданной
уравнением
,
то материальная
точка движется по траектории, заданной
уравнением
![]()
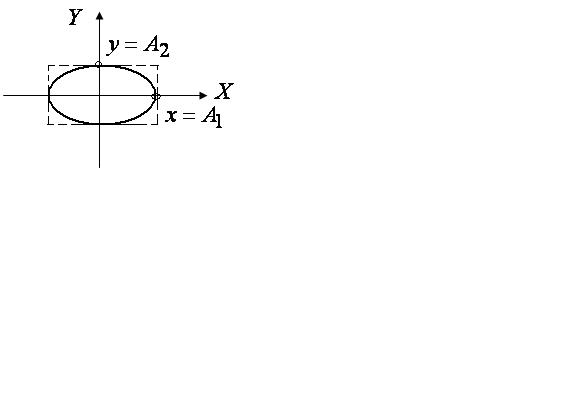
Это уравнение эллипса,
расположенного симметрично относительно
осей координат (рис.2.8). Если при разности
фаз,
,
амплитуды равны (![]() ),
то материальная
точка движется по траектории (рис.
2.9), заданной
уравнением окружности.
),
то материальная
точка движется по траектории (рис.
2.9), заданной
уравнением окружности.
![]()
|
|
Рис. 2.8 |
Рис. 2.9
|
Фигурами Лиссажу называются траектории материальной точки, которые получаются при сложении взаимно перпендикулярных колебаний.