Затухающие колебания. Дифференциальное уравнение, его решение. График. Логарифмический декремент затухания.

В природе все происходящие колебания реальные, т.е. при их рассмотрении нельзя пренебрегать силой трения: . На преодоление силы трения расходуется полная механическая энергия колеблющегося тела. Поэтому с течением времени амплитуда колебаний уменьшается до нуля, колебания прекращаются и тело возвращается в положение равновесия.

Затухающие колебания материальной точки происходят под действием двух сил: возвращающей силы и силы трения , где - коэффициент трения, - скорость.

Уравнение движения колеблющегося тела в векторной форме:

уравнение движения в скалярной форме:

Дифференциальное уравнение затухающих колебаний:

,

где - коэффициент затухания.

Решение дифференциального уравнения:

или ,

где - круговая частота колебаний, при .

- начальная амплитуда колебаний.

- амплитуда затухающего колебания.

Период затухающих колебаний:

График затухающих колебаний (рис.2.1). На практике степень затухания характеризуют логарифмическим декрементом затухания, который показывает в логарифмическом масштабе во сколько раз амплитуда в любой момент времени больше амплитуды через период .

Вынужденные колебания. Дифференциальное уравнение. Решение. Резонанс.

Вынужденными колебаниями называются незатухающие колебания, возникающие в колеблющейся системе под действием внешней переменной силы. Внешняя сила постоянно подает энергию в колебательную систему, чтобы компенсировать потери энергии на преодоление силы трения. Внешняя сила должна удовлетворять следующим условиям:

1. должна быть периодической, т.е. изменяться по закону sin или cos

, где - амплитудное значение внешней силы.

2. частота внешней силы не должна быть равной собственной частоте колебаний материальной точки:

Вынужденные колебания происходят под действие трех сил: возвращающей силы, силы трения и внешней силы. Уравнение движения в векторной форме:

.

Дифференциальное уравнение вынужденных колебаний:

Решением данного уравнения является функция:

Итак, вынужденные колебания осуществляются с частотой, равной частоте внешней силы. Амплитуда вынужденных колебаний:

т.е. амплитуда вынужденных колебаний зависит от амплитуды и круговой частоты внешней силы .

Резонансом называется явление резкого увеличения амплитуды вынужденных колебаний, при приближении частоты внешней силы к собственной частоте колеблющегося тела.

Происходящие при этом колебания называют резонансными колебаниями, а их частота - резонансной частотой:

, если , то .

А мплитуда при резонансе:

График зависимости амплитуды вынужденных колебаний от частоты внешней силы называется резонансной кривой (рис. 2.2.).

Автоколебания.

Автоколебательная система – колебательная система, которая берет энергию извне только тогда, когда это необходимо. В такой системе возникают автоколебания.

Автоколебания – незатухающие колебания, поддерживаемые за счет внешнего источника энергии. Однако, моменты времени в которые осуществляется подача энергии, амплитуда и частота колебаний определяются свойствами самой колебательной системы и не зависят от характеристик источника энергии. В простейших автоколебательных системах можно выделить: источник энергии, колебательную систему с затуханием, регулятор и систему обратной связи.

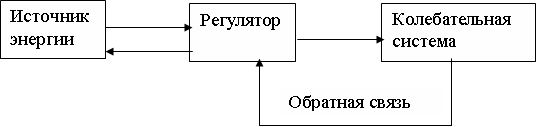
Рис. 2.3.

Примеры автоколебательных систем: сердце и легкие.