Вязкость жидкости.

При течении реальной жидкости между молекулами действуют силы взаимного притяжения, в результате чего возникает внутреннее трение (вязкость).

Формула Ньютона: , где - сила внутреннего трения между двумя слоями жидкости, она ускоряет медленно текущие слои и замедляет быстротекущие слои, направлена сила трения по касательной к поверхности соприкасающихся слоев; коэффициент внутреннего трения (коэффициент вязкости), площадь соприкосновения слоёв, - градиент скорости - показывает на сколько изменяется скорость при изменении толщины слоя на единицу.

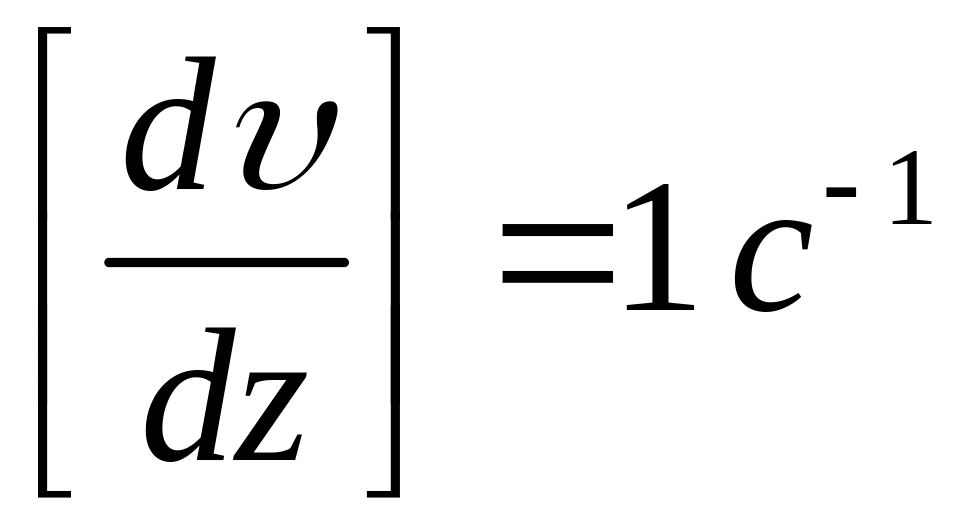
Физический смысл коэффициента внутреннего трения: 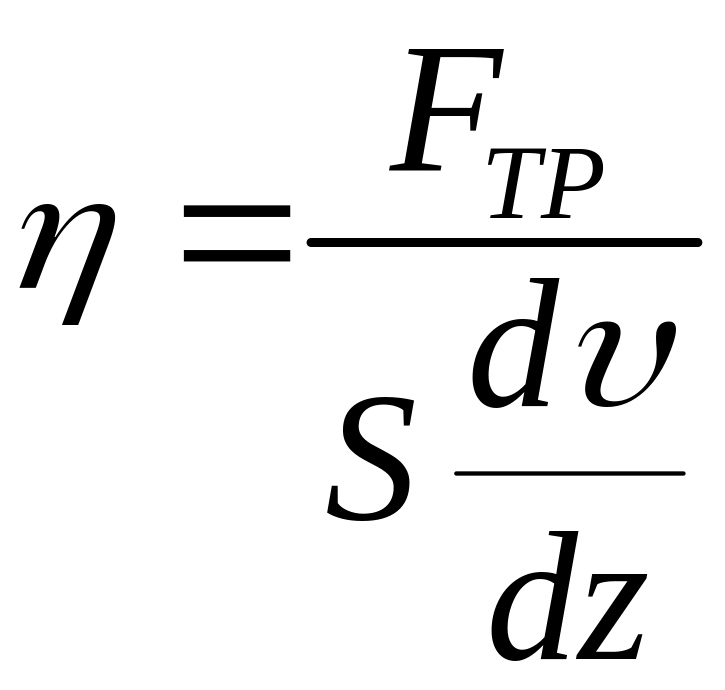-коэффициент внутреннего трения показывает, какая сила трения возникает при соприкосновении слоев на площади, равной 1 м², при градиенте скорости между ними, равном 1 с^-1.

Внесистемной единицей является 1 Пуаз; 1 П = 0,1 Па ·с

Ламинарное и турбулентное течение

Ламинарное течение – течение, при котором слои жидкости движутся параллельно друг другу не смешиваясь между собой. Ламинарное течение наблюдается при небольших скоростях течения в трубках с гладкими стенками, без резких изменений площади сечения и без разветвлений.

Турбулентное течение – течение, при котором слои жидкости перемешиваются, образуя вихри. Скорости молекул жидкости беспорядочно меняются, молекулы жидкости переходят из слоя в слой, за счет этого происходит перемешивание жидкости. Турбулентное течение сопровождается шумами.

Характер течения жидкости определяется числом Рейнольдса

,

где - скорость течения жидкости, - плотность жидкости, - диаметр трубы, - вязкость жидкости.

Существует критическое число Рейнольдса ( ). Если возможно только ламинарное течение, если возможно только турбулентное течение. Для однородной жидкости критическое число Рейнольдса

, для крови - (в зависимости от диаметра сосуда).

Распределение скорости и градиента по сечению трубы при ламинарном течении.

Р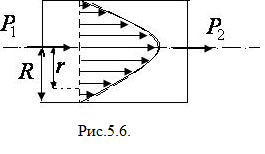 ассмотрим ламинарное течение вязкой жидкости по горизонтальной трубе постоянного сечения (рис. 5.6.). Распределение скорости по сечению трубы носит параболический характер:

,

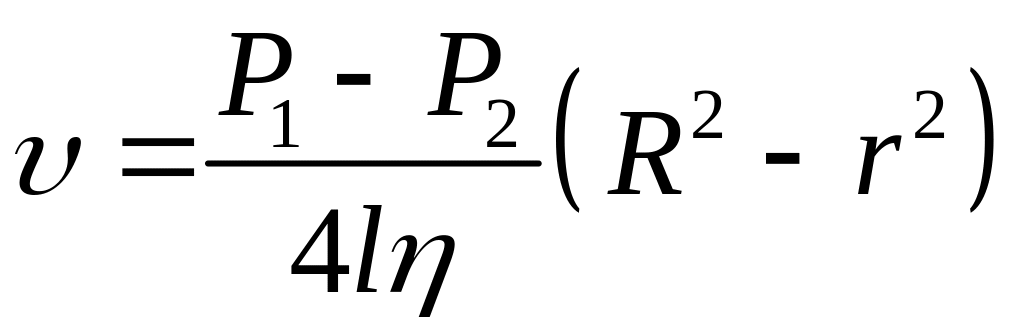где - радиус трубы, радиус рассматриваемого слоя, длина трубы, и – давление в начале и конце трубы, соответственно.

Скорость имеет наибольшее значение в центре трубы:

, .

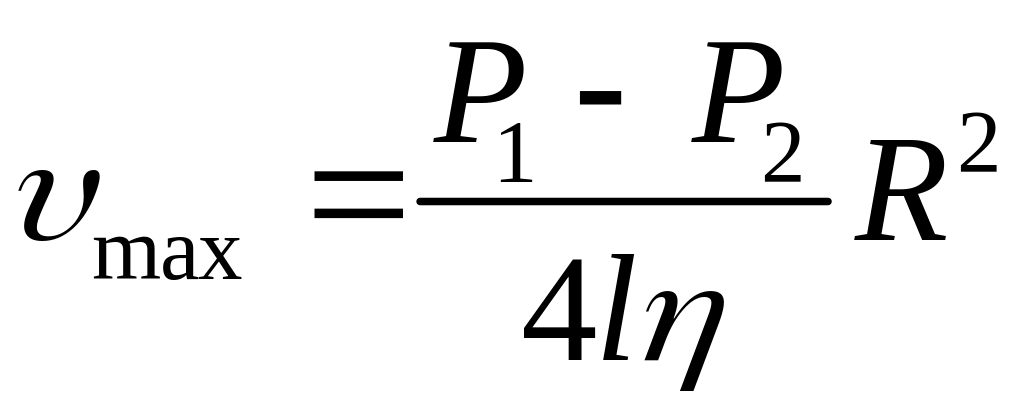Градиент скорости максимален в пристеночной части трубы:

.

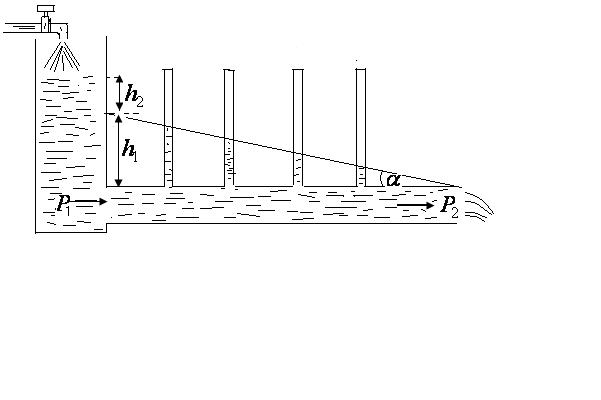
Течение реальной жидкости по горизонтальной трубе постоянного сечения. Закон Гагена - Пуазейля.

При течении жидкости по горизонтальной трубе постоянного сечения (рис. 5.7.) потенциальная энергия её частиц расходуется на работу по преодолению внутреннего трения. Поэтому статическое давление вдоль трубы постепенно падает. Высота соответствует начальному статическому давлению, а высота – гидродинамическому давлению, обеспечивающему скорость течения жидкости. Крутизна этой кривой (тангенс угла наклона) характеризует продольный градиент давления: .

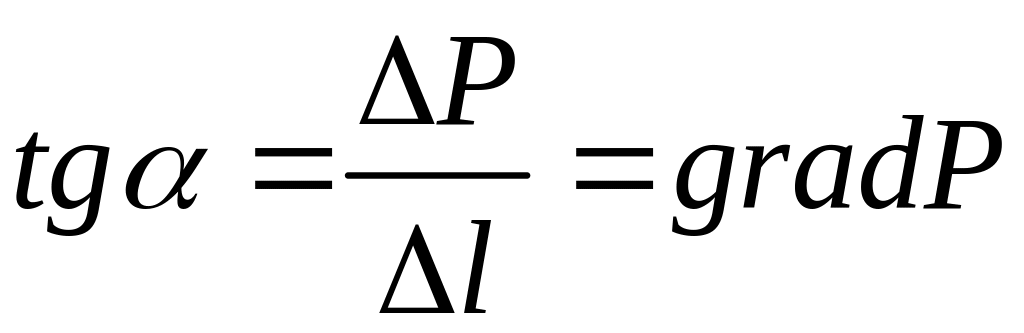
Рис.5.7. Пуазейль определил среднюю скорость течения жидкости по горизонтальной трубе постоянного сечения: 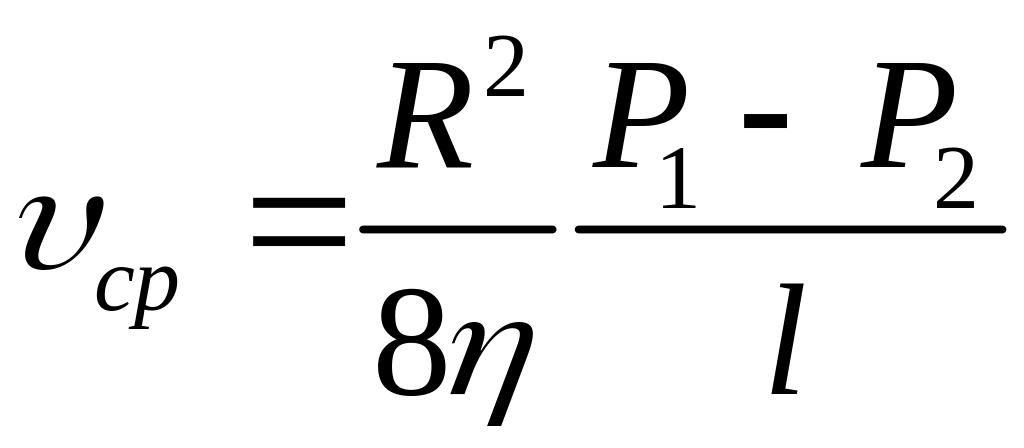– закон Пуазейля. Количество жидкости, протекающей через поперечное сечение за единицу времени

- закон Гагена-Пуазейля.