
- •Тема 1. Введение Материя и формы ее движения. Значение физики в медицине.
- •Классификация медицинской электронной аппаратуры
- •Классификация медицинской электроники по функциональному назначению:
- •II. Классификация медицинской аппаратуры по принципу действия.
- •Действие электрического тока на организм.
- •Обеспечение электробезопасности при работе с медицинской аппаратурой.
- •Основные требования электробезопасности
- •Классификация медицинской аппаратуры по способу дополнительной защиты от поражающего действия электрического тока.
- •Надежность медицинской аппаратуры
- •Тема 2. Механические колебания
- •Основные определения и характеристики колебательного процесса.
- •Дифференциальное уравнение, решение. График.
- •Полная энергия колеблющейся точки.
- •Затухающие колебания. Дифференциальное уравнение, его решение. График. Логарифмический декремент затухания.
- •Вынужденные колебания. Дифференциальное уравнение. Решение. Резонанс.
- •Автоколебания.
- •Сложение гармонических колебаний, направленных вдоль одной прямой.
- •Сложение взаимно перпендикулярных колебаний.
- •Сложное колебание. Гармонический спектр сложного колебания. Теорема Фурье.
- •Тема 3 механические волны.
- •Уравнение плоской механической волны.
- •Энергия волны. Поток энергии волны. Вектор Умова.
- •Эффект Доплера.
- •Тема 4. Акустика. Природа звука.
- •Физические характеристики звука.
- •Характеристики слухового ощущения (Физиологические характеристики).
- •Шкала уровней громкости.
- •Звуковые методы исследования в клинике.
- •Тема 5. Гидродинамика
- •Уравнение неразрывности струи
- •Уравнение Бернулли
- •Практические следствия из уравнения Бернулли.
- •Вязкость жидкости.
- •Ламинарное и турбулентное течение
- •Распределение скорости и градиента по сечению трубы при ламинарном течении.
- •Течение реальной жидкости по горизонтальной трубе постоянного сечения. Закон Гагена - Пуазейля.
- •Течение жидкости по горизонтальной трубе переменного сечения
- •Течение жидкости по разветвленной трубе
- •Течение жидкости по трубе с эластичными стенками
- •Тема 6. Биореология.
- •Зависимость коэффициента вязкости крови
- •Физические модели кровообращения.
- •Закономерности выброса и распространения крови в большом круге кровообращения.
- •Работа и мощность сердца.
- •Тема 7. Биологические мембраны Значение и функции биологических мембран. Строение мембран.
- •Физиологические функции мембран.
- •Физические свойства мембран.
- •Модели искусственных мембран для изучения свойств мембран.
- •Методы исследования мембран
- •1. Микрокалориметрия.
- •3. Люминесцентный анализ.
- •4. Рентгеноструктурный анализ.
- •5.Электронный парамагнитный резонанс (эпр).
- •6.Ядерный магнитный резонанс (ямр)
- •Диффузия в жидкостях. Закон Фика.
- •Пассивный транспорт веществ.
- •Перенос незаряженных частиц (атомов и молекул) через мембрану
- •Перенос заряженных частиц (ионов) через мембрану.
- •3. Облегченная диффузия.
- •Активный транспорт.
- •Тема 8. Электромагнитные явления в биологических системах.
- •Равенство Доннана.
- •Потенциал покоя
- •Потенциал действия.
- •Распространение потенциала действия. (проведение возбуждения по нервным волокнам).
- •Тема 9. Биофизические принципы исследования электрических полей в организме.
- •2. Электрический дипольный момент диполя
- •Напряженность электрического поля диполя.
- •Потенциал. Разность потенциалов.
- •Диполь в электрическом поле.
- •Токовый диполь. Эквивалентный электрический генератор.
- •Тема 10. Электрокардиография
- •Метод отведений Эйнтховена
- •Блок-схема кардиографа.
- •Вектор-электрокардиография.
- •Тема 11. Электродинамика Электрические колебания.
- •Колебательном контуре.
- •Незатухающие электромагнитные колебания.
- •Затухающие колебания
- •Вынужденные колебания.
- •Тема 12. Импульсные токи Апериодический разряд конденсатора
- •Характеристики импульсных токов.
- •6. Коэффициент заполнения
- •Генераторы импульсных токов.
- •Изменение формы импульса.
- •Дифференцирующая цепь
- •Интегрирующая цепь.
- •Действие импульсного тока на ткани организма
- •Тема 13.
- •Биологические основы реографии
- •Цепи переменного тока, содержащие отдельные элементы
- •Цпт, содержащая последовательно включенные активное, индуктивное и ёмкостное сопротивления
- •Цепь переменного тока, содержащая параллельно включенные активное, индуктивное и ёмкостное сопротивления
- •Тема 14. Электромагнитное поле. Электромагнитные волны
- •Основные положения электромагнитной теории Максвелла.
- •Уравнение электромагнитной волны.
- •Энергия электромагнитной волны
- •Шкала электромагнитных волн.
- •Физические процессы, происходящие в тканях организма под действием токов и электромагнитного поля
- •3. Переменное магнитное поле.
- •Тема 15. Поляризация света
- •Методы получения полностью поляризованного света
- •При отражении от неметаллического зеркала
- •2.При двойном лучепреломлении
- •3. Дихроизм.
- •Система поляризатор – анализатор
- •Вращение плоскости поляризации. Поляриметрия.
- •Поляризационный микроскоп
- •Тема 16. Тепловое излучение. Природа теплового излучения.
- •Характеристики теплового излучения
- •Закон Кирхгофа
- •Спектр излучения ачт
- •Законы излучения абсолютно черного тела
- •Формула Планка и её применение для уточнения законов теплового излучения абсолютно черного тела
- •Тема 17 элементы квантовой физики Волновые свойства частиц. Длина волны де Бройля
- •Электронный микроскоп
- •Люминесценция
- •В зависимости от причины, вызвавшей свечение:
- •Фотолюминесценция
- •Закон Стокса
- •Применение люминесценции в медицине
- •Индуцированное излучение Лазеры – оптические квантовые генераторы
- •Свойства лазерного излучения
- •Применение лазеров в медицине
- •Голография и возможности её применения в медицине
- •Тема 18. Рентгеновское излучение
- •Свойства рентгеновского излучения
- •Механизмы генерации рентгеновского излучения
- •Рентгеновская трубка
- •Зависимость энергии рентгеновского излучения от рабочих параметров рентгеновской трубки.
- •Действие рентгеновского излучения на вещество
- •Применение рентгеновского излучения в медицине
- •Тема 19. Ионизирующее излучение
- •Строение атомного ядра
- •Модели строения ядра
- •Энергия связи
- •Радиоактивность. Виды излучений
- •Основной закон радиоактивного распада
- •Радиоактивность в природе – естественная фоновая радиация
- •Дозиметрия ионизирующего излучения Проникающая и ионизирующая способности радиоактивного излучения
- •Биофизические основы действия ионизирующего излучения на организм
- •Характеристики ионизирующего излучения
- •Дозиметрическая аппаратура
- •Защита от ионизирующего излучения
Тема 5. Гидродинамика
Гидродинамика - раздел физики, в котором изучается движение несжимаемых жидкостей. Законы гидродинамики позволяют описать движение крови по сосудам.
Идеальная жидкость - жидкость несжимаемая и не имеющая внутреннего трения или вязкости.
Стационарное или установившееся течение - течение, при котором скорости частиц жидкости в каждой точке потока со временем не изменяются.
Установившееся течение характеризуют линиями тока.
Линии тока - это воображаемые линии, совпадающие с траекториями движения частиц.
Трубка тока - часть потока жидкости, ограниченная со всех сторон линиями тока.
Уравнение неразрывности струи
В общем потоке жидкости
выделяют трубку тока настолько узкую,
что скорость частиц в любом её сечении,
перпендикулярном оси трубки, можно
считать постоянной: в сечении
![]() скорость -
скорость -
![]() ,
в сечении
,
в сечении
![]() скорость -
скорость -
![]() (рис.5.1).
(рис.5.1).
Рис. 5.1. |
|
![]() ,
т.е.
,
т.е.
![]() -
-
уравнение неразрывности струи: при установившемся течении по трубе переменного сечения количество жидкости, протекающее в единицу времени через любое поперечное сечение трубы, остается постоянным.
Уравнение Бернулли
Рассмотрим
течение идеальной жидкости по трубе
переменного сечения. Выделим в потоке
идеальной жидкости трубку тока, а в ней
достаточно малый объем жидкости
![]() ,
массой
,
массой
![]() ,
который при течении жидкости перемещается
из положения 1 в положение 2 (рис. 5.2.).
,
который при течении жидкости перемещается
из положения 1 в положение 2 (рис. 5.2.).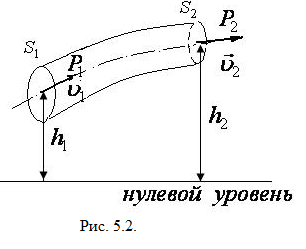
|
где
![]() – давление.
– давление.
При перемещении жидкости совершается работа:
![]()
Эта работа расходуется
на преодоление действия сил тяжести:
работа
![]() ,
и на изменение кинетической энергии
жидкости: работа
,
и на изменение кинетической энергии
жидкости: работа
![]() :
:
![]() ,
,
 .
.
Уравнение
Бернулли:  ,
,
где
![]() статическое
давление,
статическое
давление,
![]() гидростатическое
давление,
гидростатическое
давление,
![]() - гидродинамическое
давление. Уравнение Бернулли:
полное давление жидкости, равное сумме
статического, гидростатического и
гидродинамического давлений, остается
постоянным в любом сечении трубы.
- гидродинамическое
давление. Уравнение Бернулли:
полное давление жидкости, равное сумме
статического, гидростатического и
гидродинамического давлений, остается
постоянным в любом сечении трубы.
Практические следствия из уравнения Бернулли.
Р |
Определение гидростатического
давления.
Рассматривают трубу тока постоянного
сечения площадью
(рис. 5.3.), высота
сечений над нулевым уровнем энергии
различна и равна
![]() и
и
![]() ,
соответственно. Т.к. площадь сечений
одинакова, то скорость течения жидкости
и гидродинамическое давление остается
величиной постоянной. Уравнение Бернулли
принимает вид
,
соответственно. Т.к. площадь сечений
одинакова, то скорость течения жидкости
и гидродинамическое давление остается
величиной постоянной. Уравнение Бернулли
принимает вид
![]()
С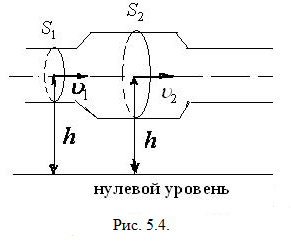 ледовательно
ледовательно
![]() .
.
![]() измеряют манометром и определяют перепад
гидростатического давления на данном
участке трубы.
измеряют манометром и определяют перепад
гидростатического давления на данном
участке трубы.
Правило Бернулли.
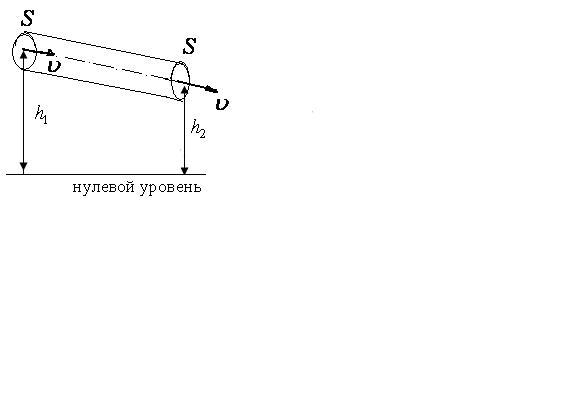
Выбирают горизонтальную трубу, имеющую
различные сечения
и
(рис. 5.4.), следовательно,
скорости
![]() и
также разные (
и
также разные (![]() ),
гидростатическое давление остается
постоянным. Уравнение Бернулли принимает
вид
),
гидростатическое давление остается
постоянным. Уравнение Бернулли принимает
вид
 ,
или
,
или

Правило Бернулли: статическое давление невязкой жидкости при течении по горизонтальной трубе возрастает там, где скорость ее уменьшается, и наоборот.
Р |
![]() ,
где
- полное давление, тогда
,
где
- полное давление, тогда
![]() .
Статическое давление жидкости
.
Статическое давление жидкости
![]() измеряют при помощи манометрической
трубки, плоскость отверстия которой
расположена параллельно движению
жидкости. Для измерения полного давления
применяют манометрическую трубку,
изогнутую под прямым углом навстречу
движения жидкости. Зная
измеряют при помощи манометрической
трубки, плоскость отверстия которой
расположена параллельно движению
жидкости. Для измерения полного давления
применяют манометрическую трубку,
изогнутую под прямым углом навстречу
движения жидкости. Зная
![]() можно определить скорость течения
жидкости:
можно определить скорость течения
жидкости:
 .
.

 ис.
5.3.
ис.
5.3.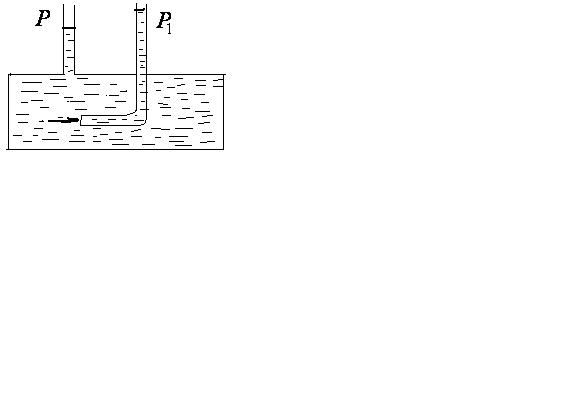 ис.
5.5.
ис.
5.5.