Лабораторная работа № 10

Тема: Численные методы решения дифференциальных уравнений.

Цель: Научиться решать дифференциальные уравнения методами Пикара, Эйлера и Рунге-Кутта.

Источники:

1. Лапчик М.П. Численные методы, М., 2004

2. Бажин И.И. Информационные системы менеджмента, М: ГУ-ВШЭ, 2000

Оборудование: ПК, ПО ЭТ Excel

Ход и содержание работы:

Часть 1:

Задание 1. Найдите методом последовательных приближений решение дифференциального уравнения , удовлетворяющее начальному условию у(0) = 2.

Вычислить y1, y2, y3 и изобразить на графике точное решение и найденную последовательность y1, y2, y3 в интервале [0;0.3]

Задание 2. Найти приближенное решение дифференциального уравнения у' = cos у + 3х методом Пикара с начальным условием у(0) = 1,3 (расчет вести до третьего приближения).

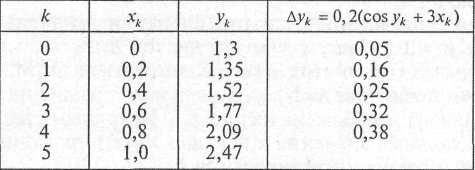
З адание 3. Решить методом Эйлера дифференциальное урав­нение у' = cos у + Зх с начальным значением у(0) = 1,3 на отрезке [0; 1], приняв шаг h = 0,2.

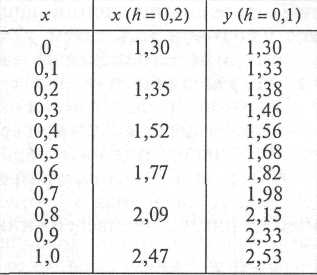
Задание 4. Методом Эйлера найти при­ближенное решение дифференци­ального уравнения , удов­летворяющее начальному условию у(0) = 1 на отрезке [0, 2] двумя способами: а) с шагом h = 0,2; б) с с шагом h = 0,1. Сопоставить точность полученных значе­ний функции.

Задание 5. Составить программу решения дифференциальных уравнений и у' = cos у + Зх ме­тодом Эйлера по приведенному на рисунке алфавиту и с заданием пользователя начального условия и интервала.

Часть 2:

Задание 1. Решить дифференциальное уравнение у' = y(1-х) на отрезке [0; 0,5] с начальным условием у(0) = 1 и шагом h = 0,05 методом Эйлера и Рунге-Кутта 4-го порядка.

Задание 2. Проведите сравнение методов Эйлера и Рунге-Кутта по результатам работы соответствующих программ (алгоритмы метода Рунге-Кутта и таблица сравнения представлена на рисунке)

З 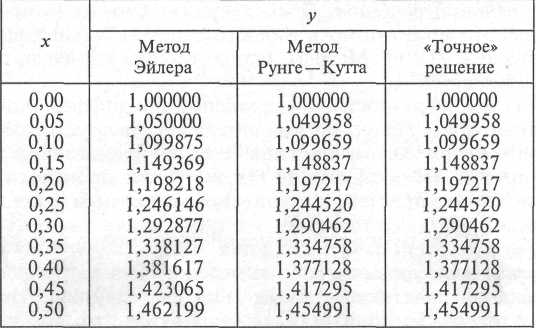адание3. Пользуясь программой для метода Рунге-Кутта, решить дифференциальное уравнение у’ = у2 + Зх с начальным условием у(1) = 3 на отрезке [1; 2] сначала с шагом h = 0,1, а затем с шагом h = 0,05. Сопоставить и проком­ментировать полученные решения.

Часть 3:

З 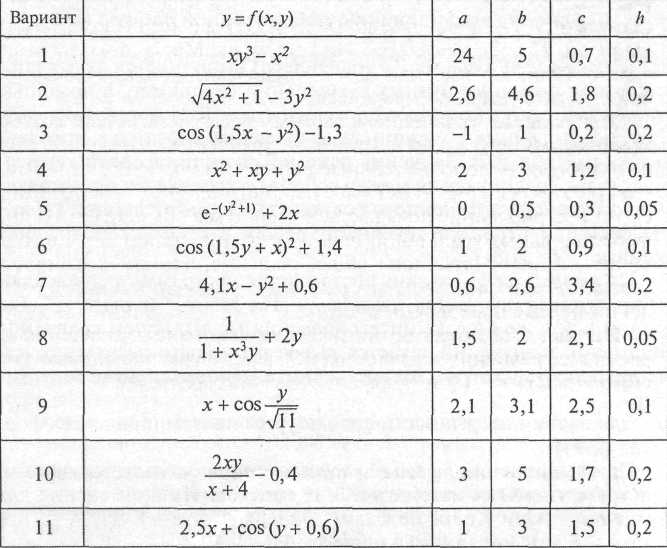адание 1. Решить задачу Коши для дифференциального уравне­ния своего варианта у = f(x,y) на отрезке [a; b] при заданном начальном условии и шаге интегрирования методами Эйлера и Рунге —Кутта с помощью Excel b программы для компьютера с шагом h.

Контрольные вопросы

1. В какой форме получается приближенное решение дифференци­ального уравнения по методу Пикара?

2. В какой форме получается при­ближенное решение дифференци­ального уравнения по методу Эй­лера?

3. В чем различие одношаговых методов Эйлера и Рунге —Кутта? Как это различие можно охарактеризовать с графической точки зрения?

Перечень литературы и технических средств обучения

1. Лапчик М.П. Численные методы. - М.: Академия, 2004.

2. Бажин И.И. Информационные системы менеджмента .- М.ГУ ВШЭ, 2000.

3. Завырыкин В.М. Численные методы. Учебное пособие для студентов. – М.: Просвещение, 1990.

4. Половнев Н.М., Якимов А.М. Системы автоматизированной обработки учетной информации. М., Фининсы и статистика, 1998.

5. Леван А. Самоучитель полезных программ. СПб.: Питер, 2000.

6. Калянов Г.Н. CASE – технологии. Консалтинг в автоматизации бизнес – процессов. М.: Горячая линия – Телескоп, 2002.

7. Шпунт Я.Б. Все необходимое для автоматизации на базе PC. ADVANTECH. Русское издание. Т., 2002.

Технические средства обучения:

1. ПК.

27