4 Характеристика нагрузок, действующих на поднимаемую систему установщиков

4.1 Виды нагрузок

Из всех операций, выполняемых при установке ракеты на пусковой стол, наиболее трудоемкой и продолжительной является перевод ракеты из горизонтального положения в вертикальное, при этом на механизм подъема стрелы (ри­сунок 1) со стороны поднимаемой системы (ПС), под которой будем понимать стрелу с ракетой или стрелу с траспортно-установочной тележкой с ракетой, действует момент сопротивления, создаваемый

ТП

Артезианские скважины водозабора

Караульное помещение

Очистные сооружения

Котельная

Склады служб тыла

Парк

Пожарное

депо

Баня

Столовая

Стадион

Тактические поля

Строевой плац

Клуб

Спортзал

Учебный

корпус

Казарма

Штаб

Предупредительное ограждение

Подъездная дорога

Гостиница

Столовая

КПП

Рисунок 10 – Схема административно-хозяйственной зоны РКК (применительно к в/ч)

весовыми, инерционными и ветровыми нагрузками. Уравнение моментов при вращательном движении поднимаемой системы под действием механизма подъема имеет вид

или

M_{M =} M_G + M_B + Mв + M_T , ( 1 )

где M_M - момент, развиваемый механизмом подъема относительно оси поворота стрелы; .

P_g - усилие гидродомкрата;

a - плечо гидродомкрата;

I - массовый момент инерции поднимаемой системы относительно оси поворота стрелы;

угловое ускорение поднимаемой системы;

јR;

ј - линейное ускорение центра тяжести системы;

R- радиус вращения центра тяжести;

M_G, M_B, M_в, M_T - моменты относительно оси поворота стрелы соответственно от сил веса, сил инерции поднимаемой системы от ветровой нагрузки, действующей на систему и от сил трения в шарнирах механизма подъема.

Для расчета основных параметров механизма подъема стрелы необходимо иметь значения всех моментов в функции угла подъ­ема стрелы, т.е.

М_G = f₁ ( φ ), M_B = f₂ (φ ), М_в = f₃ (φ ), М_T = f₄ (φ ).

Рассмотрим последовательно методики определения указанных зависимостей.

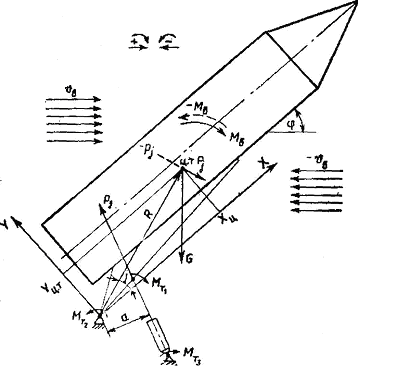
Рисунок 2 - Расчетная схема к определению нагрузки на поднимаемую систему

4.2 Грузовой момент

Момент от сил веса или грузовой момент в функции угла подъема определяется из выражений

М_G = GRcos ( ) ( 2 )

или M_G = GX_ц (cos ( 3 )

где G - суммарный вес (рисунок 2) поднимаемой системы (стрелы и ракеты),

R - расстояние от центра вращения стрелы до центра тяжести поднимаемой системы,

R = ; ( 4 )

где - текущее значение угла подъема сирелы;

- начальный угол наклона линии 00₁ к линии горизонта.

= arctg . ( 5 )

Здесь Х_Ц, Y_Ц – координаты центра тяжести поднимаемой системы.

В расчетах величину М_G определяют для нескольких значений угла

В пределах от =0 до = _max ( 90⁰ ), принимая обычно = 10⁰ ( 15⁰), и

строят кривую М_G = f₁ ( ).

Обычно из выражения (3) можно установить, что кривая М_G = f₁ ( ) представляет собой косинусоиду, следовательно, она может быть построена графически без расчета ее по точкам. Схема графического определения М_G и построения кривой М_G = f₁ ( ) приведена на рисунке 3. Для построения кривой пpинимaютcя масштабы и произведения GR..Про

водятся оси координат и М_G.. На продолжении оси на расстоянии, несколько большем, чем в принятом масштабе выбирается точка 0 и из нее как из центра радиусом r = GR описывается дуга ДАB. От вертикали ОD откладывается угол и далее угол АОВ, равный углу подъема стрелы 90⁰.

Дуга АВ делится на несколько равных частей (обычно на 6 или 9), и через точки деления проводятся горизонтальные ли­нии. На оси в принятом масштабе от качала координат откладываются соответствующие точки деления дуги АВ значения угла . Через полученные точки проводятся вертикальные линии. Пересечение соответствующих горизо-

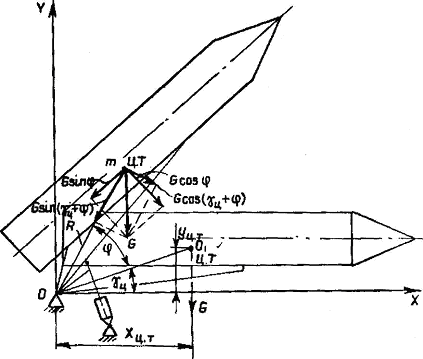
Рисунок 3 - Расчетная схема к определение грузового момента

нтальных и вертикальных линий дают точки, через которые проходит кривая М_G = f₁ ( ).

Рисунок 4 – Графическое построение кривой грузового момента

Анализ формулы ( 3 ) и кривой М_G = f₁ ( ) показывает, что грузовой момент М_G имеет максимальное значение в начале подъема системы ( =0). При = 90⁰ - линия действия силы веса поднимаемой системы проходит через ось поворота стрелы и грузовой момент равен нулю. При дальнейшем движении стрелы М_G меняет свой знак и из момента, препятствующего подъему системы, превращается в момент, способствующий ее дальнейшему движению. Под действием этого момента система стремится опрокинуться в сторону подъема, и для исключения этого к поднимаемой системе должен прикладываться момент сопротивления, уравновешивающий грузовой момент, обеспечивающий главную доводку системы до вертикального положения.