§ 5. Потенциал простого слоя

В отличие от потенциала двойного слоя, потенциал простого слоя

(1)

непрерывен во всех точках поверхности Ляпунова .

Теорема 1. Потенциал простого слоя (1) с ограниченной плотностью непрерывен во всем пространстве.

Доказательство. В точках, не принадлежащих поверхности , потенциал простого слоя имеет производные всех порядков и удовлетворяет уравнению Лапласа. Поэтому для доказательства теоремы достаточно показать, что интеграл (1) равномерно сходится в точках поверхности.

Пусть - произвольная точка поверхности. Представим потенциал (1) в виде суммы

где - достаточно малая часть поверхности, лежащая в сфере некоторого радиусас центром в точке,- оставшаяся часть поверхности. Обычным образом введем местную систему координат с началом в точкеи осью, направленной по внешней нормали к поверхности в точке. Пусть- произвольная точка, удаленная отна расстояние. Обозначим черезпроекциюна плоскость, а через– круг радиусас центром в точке, лежащей в. Полагая,и учитывая соотношения

,

,

получим

Здесь - проекциянаивзято столь малым, что.

Введем в плоскости полярную систему координатс началом в точке. Тогда

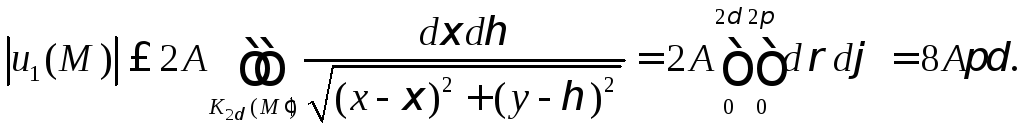
Выбирая для произвольногозначение, получим, если. Следовательно,равномерно сходится в любой точкеи является в этой точке непрерывной функцией. ■

Замечание. Для случая двух переменных имеет место аналогичная теорема.

Изучим поведение нормальных производных потенциала простого слоя. Докажем, что на поверхности нормальные производные потенциала простого слоя имеют разрыв того же типа, что и потенциал двойного слоя. Черезиобозначим соответственно внешнюю и внутреннюю нормальные производные. Исследуем разрыв внутренней нормальной производной на поверхности.

Производная в точкеоси, направленной по внутренней нормали, равна

, (2)

где – угол между осьюи вектором(рис. 28). Из точкипроведем нормальи прямую, параллельную оси(параллельную нормалив точке). Обозначим

.

Заметим, что для поверхности Ляпунова выполняются неравенства

(3)

Учитывая, чтои пользуясь известной формулой

связывающей плоские углы при вершине пирамиды и двугранный угол, образованный ее гранями (рис. 29), получим

где – двугранный угол с ребром. Отсюда и из (2) следует, что

(4)

Интеграл является функцией, непрерывной в точке, так как в силу неравенства (3) и теоремы 1 § 2 равномерно сходится в этой точке. Интегралявляется потенциалом двойного слоя с плотностью. Поэтому по теореме 2 § 4

(5)

Обозначим

где - угол между осьюи векторомТак каки осьпо условию направлена по внутренней нормали, находим

(6)

Если ось направить по внешней нормали, то знакизменится, и мы получим

(7)

Для случая двух переменных имеют место аналогичные формулы. Требуется лишь заменить на

§ 6. Применение поверхностных потенциалов к решению краевых задач

Поверхностные потенциалы дают возможность сводить краевые задачи для уравнения Лапласа к интегральным уравнениям. Такой прием эффективен при решении краевых задач со сложной границей и удобен в теоретических исследованиях. Отметим, что решение задачи Дирихле при этом ищут в виде потенциала двойного слоя, решение задачи Неймана – в виде потенциала простого слоя.

В качестве примера рассмотрим первую и вторую краевые задачи: найти функцию , гармоническую в области, ограниченной контуромГ, и удовлетворяющую либо граничным условиям задачи Дирихле (первой краевой задачи) , либо условиям задачи Неймана (второй краевой задачи)

Как для внутренней, так и для внешней задачи нормаль в граничном условии будем считать внутренней.

Решение внутренней первой краевой задачи ищем в виде потенциала двойного слоя

(1)

с неизвестной пока функцией При любом выборефункцияудовлетворяет уравнению Лапласа в области, охваченной контуромГ, и разрывна на контуре Г. Для выполнения граничных условий необходимо, чтобы в каждой точке выполнялось равенство. Поэтому по формуле (15) § 4 получим уравнение для определения:

(2)

Если в формуле (2) перейти к естественному параметру, обозначив через идуги контураГ, соответствующие точкам и, то (2) примет вид

(3)

где L – длина контура Г, - ядро интегрального уравнения. Уравнение (3) является уравнением Фредгольма второго рода. Решив его, найдем функцию, а значит, решим и внутреннюю задачу Дирихле.

Для внешней первой краевой задачи аналогично получим уравнение

(4)

Перейдем ко второй краевой задаче. Если искать ее решение в виде потенциала простого слоя

(5)

то для внутренней задачи функция определяется как решение уравнения

(6)

для внешней задачи – как решение уравнения

(7)

Ядро в интегральных уравнениях (6) и (7) имеет вид

.

Пример (первая краевая задача для круга). Решим внутреннюю задачу Дирихле для уравнения Лапласа в круге радиусаR с границей Г. Предполагая использовать формулы (1) и (2), найдем ядро

потенциала двойного слоя. Из рис. 30 ясно, что , поэтому интегральное уравнение (3) для определения функциипримет вид

(8)

Ядро этого уравнения вырожденное, т.к. зависит только от одного аргумента Поэтому легко видеть, что решением уравнения (8) является функция

, (9)

где А – некоторая подлежащая определению постоянная. Подставим функцию (9) в уравнение (8) и выразим постоянную А через заданную функцию f :

Таким образом, решением интегрального уравнение (8) является функция

Соответствующий потенциал двойного слоя, дающий решение первой краевой задачи для круга, равен

Преобразуем правую часть этой формулы, полагая, что точка М лежит внутри Г :

(10)

(Здесь было использовано равенство проверить которое предлагается читателю).

Преобразуем подынтегральное выражение. Из треугольника(рис. 31)и. Отсюда

Подставив найденное выражение в (10), получим известную формулу Пуассона для круга

дающую решение задачи (см. § 4 гл. V).

Задача 1. Методом потенциалов решить задачу Дирихле для уравнения Лапласа:

1) в полуплоскости; 2) в полупространстве.

Задача 2. Решить уравнение Лапласа внутри круга радиусаR при граничных условиях: 1) 2).

Задача 3. Решить уравнение Лапласа внутри прямоугольникапри граничных условияхс произвольными кусочно-непрерывными функциямии