§ 4. Потенциал двойного слоя

Потенциалы простого и двойного слоев в точках поверхности интегрирования являются несобственными интегралами. Далее будет доказано, что на классе поверхностей, называемых поверхностями Ляпунова, эти интегралы сходятся, если плотности потенциалов ограничены.

Определение. Замкнутую поверхность называют поверхностью Ляпунова, если выполнены следующие условия:

1) В каждой точке поверхности существует нормаль (касательная плоскость);

2) Существует такое единое для всех точек поверхности число , что прямые, параллельные нормали в какой-либо точкеP поверхности Ф, пересекают не более одного раза часть поверхностиФ, лежащую внутри сферы радиуса с центром в точкеP. Участок поверхности называется окрестностью Ляпунова точки.

3) Острый угол , образованный нормалями в любых точкахиповерхностиФ, удовлетворяет условию

,

где - расстояние между этими точками,A и – постоянные, не зависящие от выбора точек.

Пусть – произвольная точка поверхности ЛяпуноваФ. В силу условия 1) можно ввести местную прямоугольную систему координат с началом в точке . Осьнаправим вдоль внешней нормали, тогда плоскостьсовпадет с касательной плоскостью к поверхностиФ в точке . В силу условия 2) в этой местной системе координат часть поверхностилежащую внутри сферы радиусас центром в, можно задать уравнением, разрешенным относительно:

Из условий 1) и 3) следует, что частные производные исуществуют и непрерывны. Установим некоторые оценки для функциии ее производных.

Направляющие косинусы внешней нормали в точкевыражаются формулами

(1)

В силу выбора системы координат . Возьмем числостоль малым, что

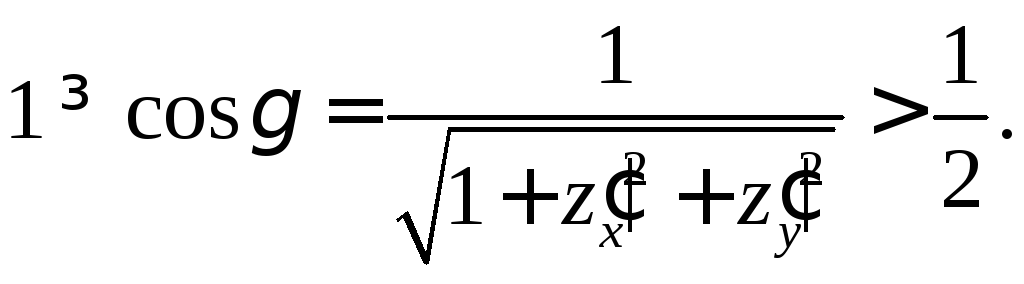(2)

Обозначим через проекцию векторана плоскость, а черези- углы, образованные векторомс осямии. Ясно, что

, .

Так как , то в силу условия 3)

и, следовательно,

Из (1) получаем ,, из (2) следует неравенство. Поэтому,. Пользуясь формулой Тейлора для функциив окрестности точки, имеем

где ,. Отсюда

(3)

Приступим к изучению свойств потенциала двойного слоя

(4)

с непрерывной плотностью , распределенной по поверхности Ляпунова. Производнаяберется по направлению внешней нормалик поверхностив точке, вектор,,- произвольная точка пространства, не лежащая на поверхности. Как показано в § 1, в этом случае потенциал двойного слоя определен, удовлетворяет уравнению Лапласа и имеет производные всех порядков. Покажем, что.

Возьмем начало координат внутри конечной области, ограниченной поверхностью. Обозначим,,- наибольшее расстояние точек поверхностиот начала координат. Тогда, откуда. Считаем, что точканастолько удалена от начала координат, что, т.е.. Тогдаили. Поэтому

где .

Пусть теперь точка лежит на поверхности,. Если, тои интеграл (1) несобственный. Покажем, что он сходится.

Теорема 1. Если в (4) функция непрерывна и- поверхность Ляпунова, то интеграл (4) сходится в любой точке.

Доказательство. Для доказательства достаточно исследовать сходимость интеграла на части поверхности, находящейся внутри сферы радиусас центром в точке. На оставшейся части поверхности интеграл, очевидно, имеет конечное значение.

Введем местную систему координат с началом в точке и представим уравнение поверхностив окрестности точкив виде. Функцияудовлетворяет оценкам (2) и (3). Оценим, где- угол между внутренней нормалью в точкеи вектором. Обозначим. Тогда

.

Отсюда

(5)

Введем на плоскости полярные координаты,. Так как, то переход в интеграле к полярным координатам приводит к равенству

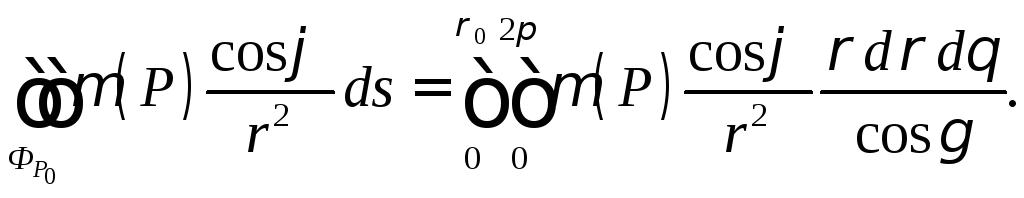(6)

Если , то для подынтегральной функции в силу (2) и (5) получим оценку

так как . Такой вид мажорантной функции достаточен для сходимости несобственного интеграла (6) (см. § 2), а значит, и интеграла (4).■

Следствие. Потенциал двойного слоя непрерывно зависит от точкиесли

Таким образом, потенциал двойного слоя определен во всем пространстве.

Замечание. В случае двух независимых переменных потенциал двойного слоя (8) § 1 сходится в точках кривой , если- кривая Ляпунова, определяемая условиями, аналогичными условиям 1) - 3) для поверхностей Ляпунова.

Если точка лежит на поверхности, например, совпадает с точкой, то значение интеграла (4) в этой точке называетсяпрямым значением потенциала двойного слоя.

Если точка находится вне поверхности, приближается к точкеи пределсуществует и конечен, то говорят, что потенциал двойного слоя принимает в точкепредельное значение. Оказывается (см. далее), что предельные и прямые значения потенциала двойного слоя, вообще говоря, не совпадают. Кроме того, предельные значения потенциала двойного слоя зависят от того, изнутри или извне стремится точка к поверхности. Это означает, что потенциал двойного слоя (4) терпит разрыв при переходе через поверхность.

Для доказательства высказанных утверждений рассмотрим сначала потенциал двойного слоя при , т.е.

(7)

Рассмотрим три случая.

1. Если точка находится вне замкнутой поверхности, то есть в бесконечной области с границей, тоесть гармоническая функция внутри, т.е. в конечной области, ограниченной поверхностью. Кроме того, функцияимеет производные всех порядков вплоть до границыи по формуле Грина (7) § 4 гл.I

2. Пусть точка находится внутри. Окружим её сферойс центром вмалого радиуса. В части пространства, лежащей междуи, функциягармоническая и по формуле Грина

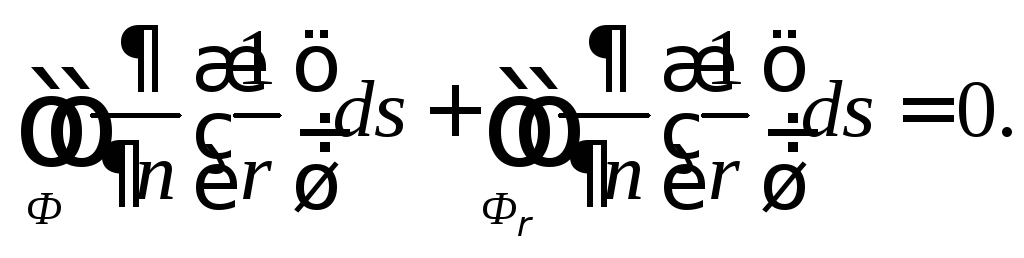(8)

В точках сферы внешняя нормаль по отношению к области направлена противоположно радиус-вектору точки. Поэтому

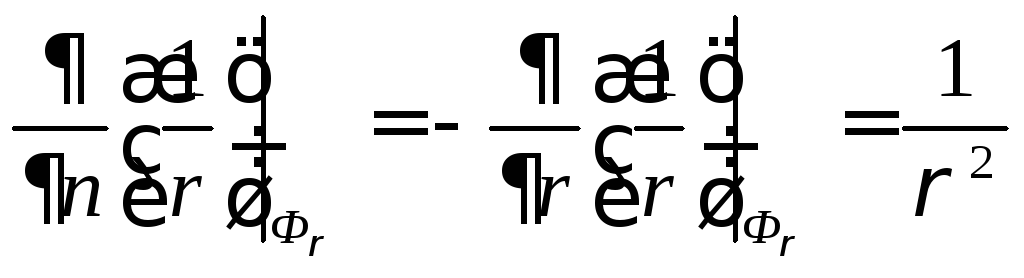
и формула (8) принимает вид

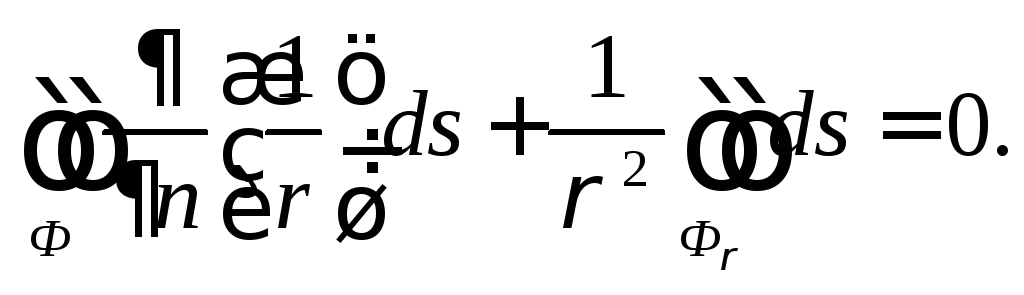
Так как последний интеграл равен , получим

3. Пусть, наконец, точка лежит на поверхности. Найдем прямое значение потенциала. Введенная ранее сферарадиусавырежет частьповерхности Ляпунова. Оставшуюся часть поверхности обозначим через. По определению несобственного интеграла

(9)

Пусть - часть сферы, лежащая внутри поверхности. Рассмотрим область, ограниченную поверхностямии. Так как точканаходится вне рассматриваемой области, то функцияв этой области гармонична и

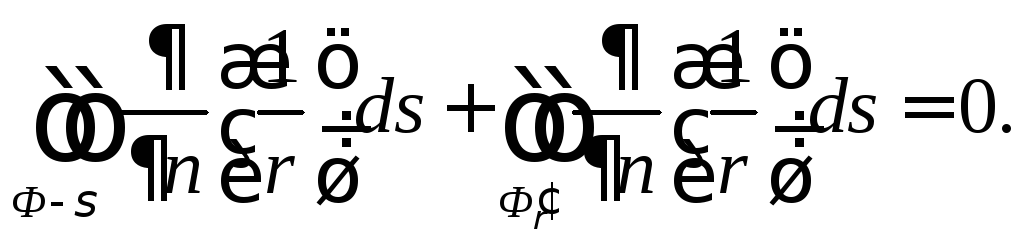
Учитывая (9), получим

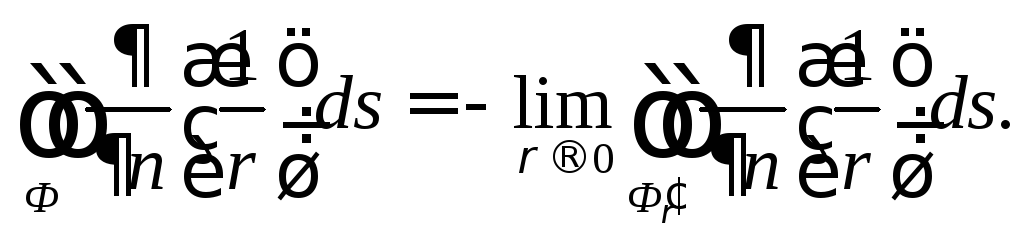(10)

Введем сферические координаты с центром в точке . Так как

, ,

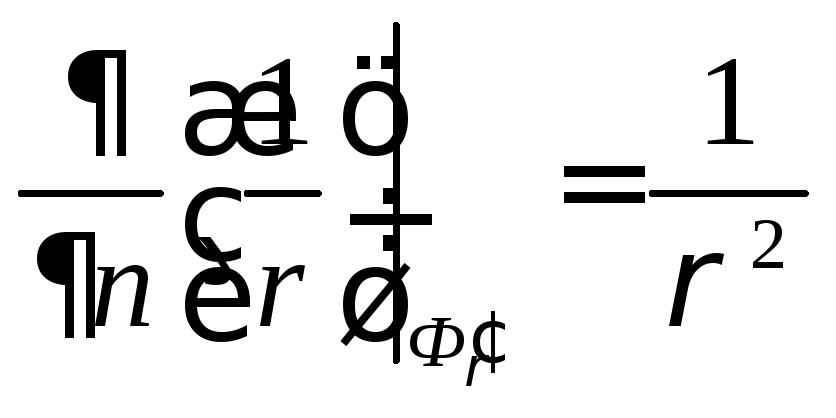имеем равенство

(11)

Покажем, что Введем рассмотренную ранее местную систему координат с началом в точке. Тогда

(12)

Заметим, что точки с координатами лежат на линии пересечения сферыс поверхностью ЛяпуноваПоэтому имеет место оценка (см. формулу (3))Отсюда и из (12) следует, что

,

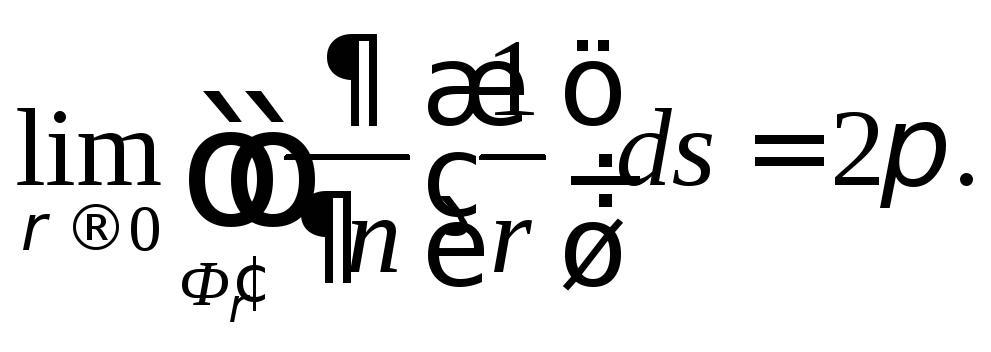причем эта сходимость не зависит от точки , т.е. равномерная. Значити из формулы (11) имеемИз формулы (10) получаем искомое равенство

Соберем вместе полученные в 1-3 результаты:

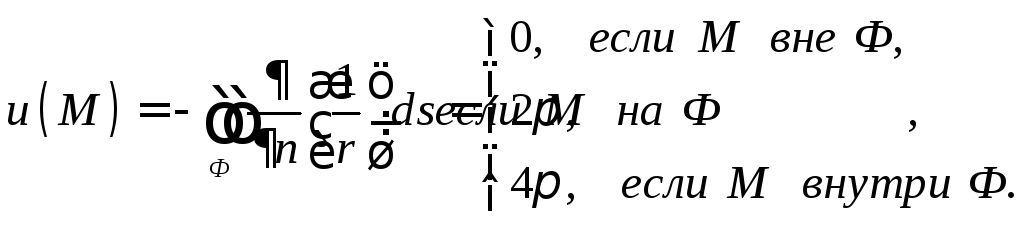(13)

Интеграл (13) называется интегралом Гаусса и является разрывной функцией.

Аналогичный результат имеет место и для произвольной непрерывной плотности .

Теорема 2 ([28], гл.VI. § 31). Потенциал двойного слоя имеет конечные пределы при стремлении точкик точкеповерхностикак изнутри, так и снаружи. Если пределснаружи обозначить через, а предел изнутри - через, то имеют место формулы

,

,

где - угол, образованный вектороми нормальюв переменной точке

Аналогичные результаты имеют место и для потенциала двойного слоя в случае двух переменных:

(14)

Задача 1. Доказать, что для потенциала (14) при справедливы равенства:

Задача 2. Доказать, что для потенциала (14) справедливы формулы:

(15)

(обозначения те же, что использованы в теореме 2).

Задача 3. Доказать теорему 2.