§ 2. Несобственные интегралы, зависящие от параметра

Приведем основные сведения о несобственных интегралах, зависящих от параметра, которые потребуются для изложения теории потенциала.

Теорема 1. Пусть в конечной области определена функцияточки, непрерывная всюду за исключением точки, в окрестности которой функция становится неограниченной. Пусть. Если функцияудовлетворяет неравенству, гдеи, то несобственный интеграл

сходится абсолютно. Если , интегралрасходится.

Доказательство очевидно. ■

Для области аналогично интегралабсолютно сходится при ирасходится при .

Определение 1. Говорят, что интеграл

(1)

сходится равномерно в точке , если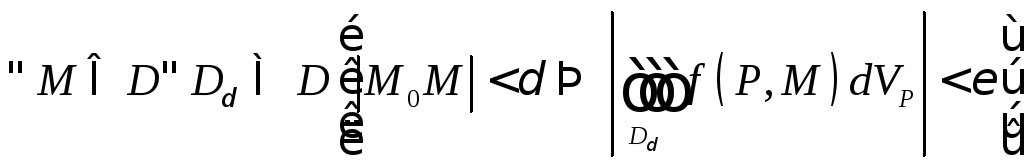. Здесь - область, содержащая точкуи имеющая диаметр, не превосходящий.

Для определение аналогично.

Теорема 2. Если интеграл (1) равномерно сходится в точке , то он определяет функцию, непрерывную в точке.

Доказательство. Пусть интеграл (1) равномерно сходится в точке . Согласно определению 1, возьмем любоеи область, содержащую точку. Интеграл (1) разобьем на два слагаемых:

Тогда

(2)

Так как точки инаходятся в области, то в силу равномерной сходимости интеграла (1),. В интегралеинтегрирование ведется по области, не содержащей точку. Поэтому функцияв точкеи некоторой её окрестности непрерывна и для всехдостаточно близких к, имеем.Подставив найденные оценки в (2), получим . Отсюда, в силу произвольности, следует непрерывность интеграла (1).■

Аналогичные рассуждения можно провести для поверхностного интеграла

(3)

Если функция непрерывна приии обращается в бесконечность при, то интеграл (3) является непрерывной функцией точкипри.

Если , токак функция точкинепрерывна на поверхностивсюду, кроме точки, в окрестности которойстановится неограниченной.

Определение 2. Пусть - область поверхности, содержащая точку Если предел

при стягивании области к точке существует, конечен и не зависит от выбора , то он называетсянесобственным интегралом от функции по поверхности Интеграл называется абсолютно сходящимся, если сходится интеграл

Ясно, что если интеграл абсолютно сходится, то он сходится.

Очевидным образом переформулировав определение 1, получим определение равномерной сходимости интеграла (3) в точке .

Теорема 3. Равномерно сходящийся в точке интеграл (3) является функцией от , непрерывной в точке.

Задача. Повторив рассуждения теоремы 2, доказать теорему 3.

§ 3. Объемный потенциал

Рассмотрим объемный потенциал

, (1)

где - конечная область, плотность- ограниченная и интегрируемая вфункция. Интеграл (1) является собственным, если. В этом случае функциянепрерывна и имеет непрерывные частные производные всех порядков, которые могут быть получены дифференцированием под знаком интеграла. Кроме того, удовлетворяет уравнению Лапласа вне области.

Теорема 1. Пусть функция определена формулой (1). Тогда , где,- расстояние точкиот начала координат.

Доказательство. Поместим начало координат внутрь области . Черезобозначим диаметр области. Тогдаили. Считая, что, т.е., получимили. Теперь

где .■

Следствие. Из полученной оценки следует, что . Отсюда и из проведенных ранее рассуждений получаем, чтообъемный потенциал (1) вне области есть гармоническая функция.

Задача 1. Проверить, что вне области логарифмический потенциал поверхности

удовлетворяет уравнению Лапласа.

Пусть теперь . Тогда интеграл (1) несобственный, причем в силу ограниченности функциии теоремы 1 § 2 интеграл (1) сходится. Кроме того, справедливы следующие важные утверждения.

Теорема 2 ([28], гл. 6, § 29). Если ограниченная и интегрируемая в функция, то объемный потенциал и его частные производные первого порядка непрерывны во всем пространстве , причем частные производные могут быть получены дифференцированием под знаком интеграла (1).

Теорема 3 ([28], гл. 6, § 29). Если плотность непрерывна в конечной замкнутой области и имеет непрерывные производные первого порядка в, то вобъемный потенциал (1) имеет непрерывные производные второго порядка и удовлетворяет уравнению Пуассона

(2)

Следствие. Если функция непрерывна ви имеет непрерывные частные производные первого порядка в, то уравнение Пуассона имеет частное решение

Так как общее решение уравнения Пуассона можно представить как сумму какого-нибудь его частного решения и общего решения соответствующего однородного уравнения, то теорема 3 позволяет свести решение краевой задачи для уравнения Пуассона к решению аналогичной, но более простой краевой задачи для уравнения Лапласа.