§ 10. Метод разделения переменных

Для простых областей (круг, прямоугольник, шар, цилиндр и ряд других) решение краевой задачи для уравнения Лапласа можно найти методом разделения переменных. Получающиеся при этом задачи на собственные значения (задачи Штурма – Лиувилля) приводят к различным классам специальных функций (сферическим, цилиндрическим и др.).

В качестве примера рассмотрим внутреннюю и внешнюю задачи Дирихле для круга. Задачу естественно решать в полярной системе координат, где оператор Лапласа имеет вид

1. Внутренняя задача Дирихле для круга. Найдем функцию , гармоническую внутри кругаи принимающую на границезаданные значения:

(1)

(2)

Решение ищем в виде произведения

(3)

Подставив (3) в уравнение (1) и разделив переменные, получим

с неопределенной постоянной . Отсюда получаем два уравнения:

(4)

(5)

Так как , то функциядолжна быть- периодической. Поэтому в (4) параметри. Кроме того, для периодичности должно выполняться равенство. Таким образом, получаем набор решений уравнения (4):

Решение уравнения (5) ищем в виде . Подставивв (5) и сократив на, получим или. Тогда

,

где и- постоянные. Ясно, что для решения внутренней задачи следует взять(для внешней задачи условие регулярности на бесконечности функции приводит к равенству ). Отсюда

(6)

Для определения коэффициентов ииспользуем граничное условие (2). Предполагая, что функциядопускает разложение в ряд Фурье, сходящийся на промежутке, запишем

(7)

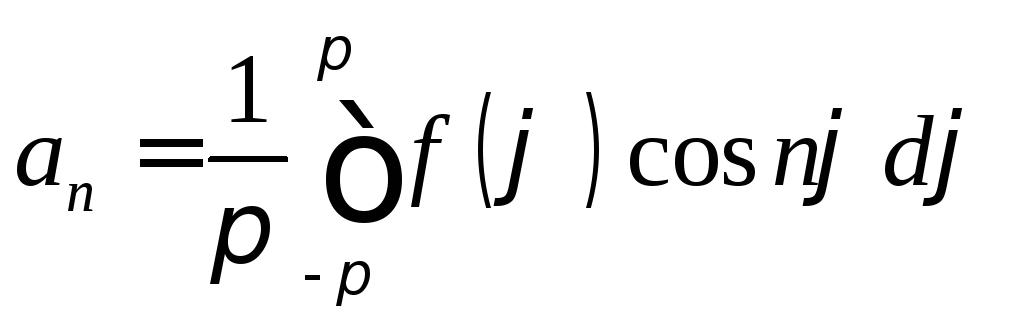
где ,. Положив в (6)и приравняв полученный ряд и ряд (7), найдем коэффициенты,,и получим формальное решение внутренней задачи Дирихле для круга:

(8)

Легко видеть, что ряд (8) сходится в круге , допускает почленное дифференцирование любое количество раз и сходится кпри. Поэтому формула (8) дает решение задачи (1) – (2).

2. Решение внешней задачи Дирихле для круга радиуса при том же краевом условии (2) дается рядом

(9)

Очевидно, что при ряд (9) сходится, допускает почленное дифференцирование любое количество раз и сходится кпри.

Задача 1. Методом разделения переменных найти функцию, гармоническую внутри единичного круга и удовлетворяющую условиюна границе:a) ; б).

Задача 2. Методом разделения переменных решить задачу Неймана:

а) для круга ; б) для области .

Задача 3. Используя результаты задачи 2, решить задачу Неймана ; 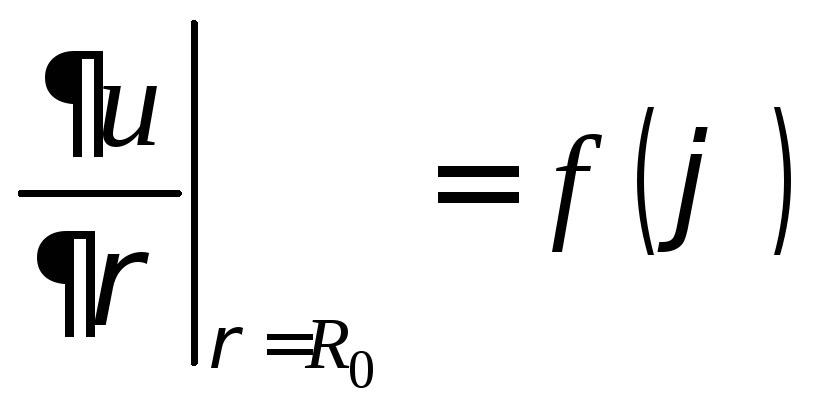для круга , если:

a) ,б).

Задача 4. Методом разделения переменных решить внутреннюю и внешнюю задачи Дирихле и Неймана для уравнения Пуассона для круга.

Задача 5. Методом разделения переменных решить внутреннюю задачу Дирихле в кольце .

Задача 6. Из формулы (8) получить формулу Пуассона (14) § 4.

§ 11. Вариационные методы решения краевых задач

Эффективные способы точного и приближенного решения краевых задач дает вариационное исчисление, позволяющее свести решение краевой задачи к задаче нахождения экстремали некоторого специально подобранного функционала. Эта последняя задача рассматривается как предельная для задачи на экстремум функции конечного числа переменных. В конечномерном (n-мерном) пространстве задача решается обычными методами, что позволяет получить приближенное решение соответствующей краевой задачи. Предельный переход приводит к точному решению краевой задачи. Не останавливаясь на обосновании (оно приведено, например, в [8], [11]), приведем алгоритмы и примеры применения двух вариационных методов – Ритца и Канторовича.

Пусть – симметричный положительно определенный оператор, действующий в вещественном гильбертовом пространстве. Несложно доказать, что уравнение

(1)

при любой правой части имеет единственное решение. Зафиксируем и определим в пространствефункционал

. (2)

Теорема 1. Для того, чтобы элемент являлся решением уравнения (1), необходимо и достаточно, чтобы функционал (2) имел принаименьшее значение.

Определение. Элементы образуютминимизирующую последовательность для функционала , если.

Теорема 2. Если А - симметричный положительно определенный оператор, то любая минимизирующая для функционала (2) последовательность сходится к решению уравнения (1).

Сформулированные теоремы показывают, что задачу решения операторного уравнения (1) можно заменить задачей о минимуме функционала (2), метод решения которой в 1908 г. предложил В. Ритц.

Суть метода Ритца в следующем. Пусть Х - сепарабельное гильбертово пространство. Выберем в Х полную систему линейно независимых (координатных) векторов . Зафиксируем произвольное натуральноеn и образуем линейную оболочку векторов. Найдем элемент, на котором функционалF имеет в наименьшее значение. Так как любой элементизможно представить в виде, то задача отысканиясводится к определениюn коэффициентов Найденные элементы(приближенные решения уравнения (1)) образуют минимизирующую последовательность для функционалаF, сходящуюся к решению уравнения (1) при

Пример 1. Решить уравнение Пуассона

(3)

внутри прямоугольника D: если на границе Г этого прямоугольника

(4)

и функция разложима внутри рассматриваемого прямоугольника в двойной ряд Фурье:

. (5)

Решение. Применив метод, рассмотренный в § 4 гл. III, легко доказать, что оператор Лапласа симметричен и положительно определен на множестве функций из , удовлетворяющих условию (4), если скалярное произведение определено равенством

Применив формулу (2), получим соответствующий оператору функционал, который с учетом формулы (3) § 4 гл.I и граничных условий (4) полезно записать в виде

(6)

(в действительности получается функционал, отличающийся от (6) знаком, но при исследовании на экстремум это отличие несущественно).

Исследуем этот функционал на экстремум методом Ритца. В качестве системы координатных функций возьмем функции

(7)

Отметим, что координатные функции следует выбирать так, чтобы они удовлетворяли граничным условиям поставленной задачи; функции (7) этим условиям удовлетворяют. Кроме того, система (7) полная и ортогональная.

В соответствии с методом Ритца возьмем

(8)

Подставив (5) и (8) в (6), получим

Ясно, что является функциейкоэффициентов, которые определяются из необходимого условия экстремума

Эта система уравнений в данном случае имеет вид

откуда

и мы получаем минимизирующую последовательность для функционала (6) или, что то же самое, последовательность приближенных решений краевой задачи (3) – (4)

Устремив ик бесконечности, получим точное решение поставленной краевой задачи (3) – (4):

Метод Канторовича отличается от метода Ритца лишь тем, что коэффициенты приближенного решенияявляются не постоянными, а функциями. В случае нескольких аргументов коэффициенты являются функциями одного из них.

Пример 2. Методом Канторовича найти приближенное решение уравнения Пуассона

(9)

в прямоугольнике , если на границе этого прямоугольника .

Решение. Уравнению (9) соответствует функционал

(10)

Первое приближение ищем в виде с координатной функциейи зависящим откоэффициентом. Функцияудовлетворяет заданному граничному условию на прямых, поэтому коэффициентследует подобрать так, чтобы он удовлетворял граничному условию при. Подставивв (10), получим функционал

(11)

Функция должна доставлять экстремум функционалу (11), т.е. быть его экстремалью.

Уравнение Эйлера для функционала

граничные условия . Решив эту граничную задачу, найдем приближенное решение уравнения (10):

Задача 1. Методом Ритца найти приближенное решение уравнения Пуассона в области, ограниченной прямыми,, если на границе области.

Задача 2. Методом Канторовича решить задачу из примера 1.

Задача 3. Методом Канторовича найти второе приближение решения уравнения (9). Приближенное решение искать в виде

.