§ 9. Применение конформных отображений к решению задач математической физики

Т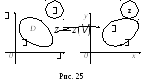еорема. Пусть аналитическая функция конформно преобразует областьплоскостив областьплоскости(рис. 25). Пусть- функция, гармоническая в. Тогда функция

гармонична в .

Доказательство. Вычислим . Имеем

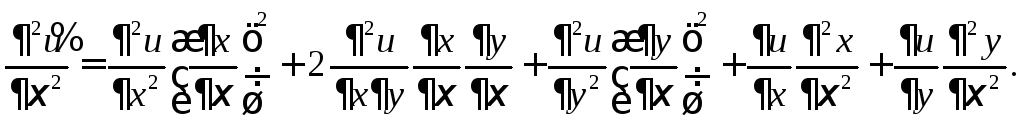
Аналогично

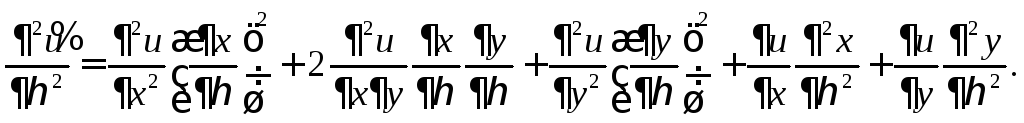
Сложим два последних равенства. При этом учтем, что иесть вещественная и мнимая части аналитической функции. Поэтомуи- гармонические функции, связанные уравнениями Коши – Римана. Следовательно, справедливы соотношения,,,. Тогда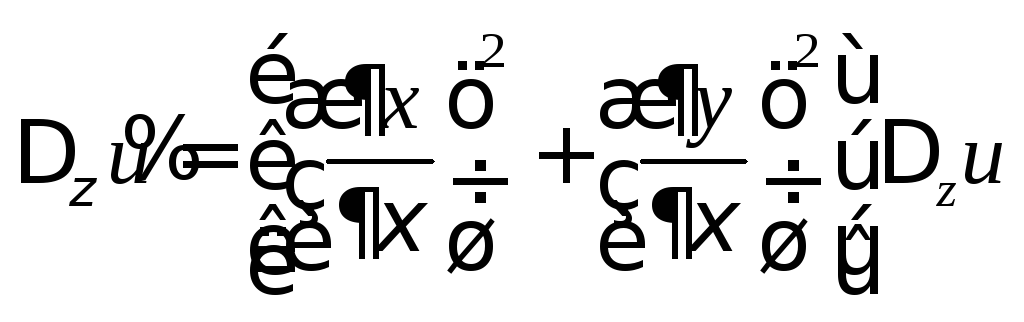, и если, то.■

Оказывается, что конформное отображение не только переводит гармоническую функцию в гармоническую, но и преобразует задачу Дирихле в задачу Дирихле, задачу Неймана – в задачу Неймана.

Действительно, пусть в области поставлена задача Дирихле

Пусть функция непрерывна в, конформно отображаетнаи контуробластина контуробласти. По доказанной теореме конформное преобразование не меняет уравнение Лапласа, поэтому преобразованная функцияудовлетворяет уравнению. А так как контуротображается на контурвзаимно однозначно, то

Отсюда следует, что преобразованная функция является решением задачи Дирихле,в области.

Задача 1. Доказать, что при конформном отображении задача Неймана переходит в задачу Неймана.

Из доказанного следует, что если известно решение задачи Дирихле или задачи Неймана для плоской области , то для решения соответствующей задачи в областидостаточно конформно отобразитьна. Если областьодносвязна и имеет достаточно гладкую границу, то задача ещё более упрощается. Достаточно отобразитьна круг или полуплоскость и воспользоваться полученными для этих областей в §§ 4, 5 формулами.

Пример. Пусть боковые стороны иполуполосышириныподдерживаются при температуре, основание- при температуре(рис. 26 а). Точкииизолированы. Найти температурув любой точке полуполосы.

Р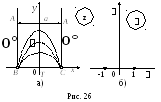ешение. Внутри полуполосы источники тепла отсутствуют, на краях температура задана, поэтому (см. § 3 гл. II) задача сводится к решению уравнения Дирихле для полуполосыс граничным условием, причем, если точкалежит на сторонахили, иесли. Заметим, что, хотя функциякусочно непрерывна, пользоваться изложенной ранее теорией (в т.ч. формулой Пуассона) можно.

Отобразим полуполосу на верхнюю полуплоскость (область) функцией(проверить!). При этом обратная функцияконформно отобразитна. Основаниеперейдет в интервал, боковые стороныи- в лучиисоответственно (рис. 26 б). Получившаяся задача Дирихле для полуплоскости нами уже решена в § 5. Воспользовавшись формулой (4) § 5, получим решение для полуплоскости:

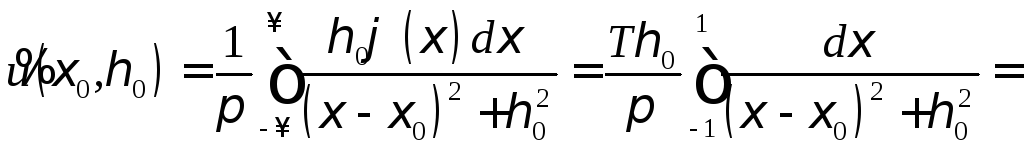
Остается найти функцию .

Используя формулу Эйлера, после несложных преобразований найдем

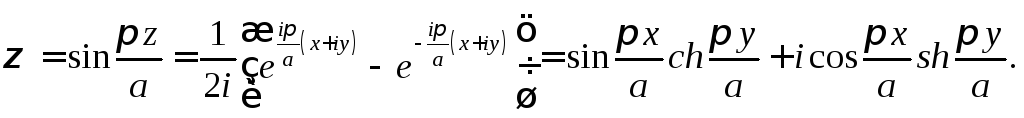
Поэтому

, .

Подставляя найденные выражения в (1) и выполняя необходимые вычисления, получим искомую функцию

.

Задача 2. Решить задачу, рассмотренную в примере, отображая полуполосу на круг и применяя формулу (12) § 4.

Задача 3. На луче сектораподдерживается постоянная температура, на луче- постоянная температура. Начало координат изолировано. Найти температуруво внутренней части сектора.

Задача 4. Найти функцию , гармоническую вне круга радиусас центром в начале координат и удовлетворяющую граничным условиям: а); б),.

Задача 5. Найти функцию , гармоническую внутри круга радиусас центром в начале координат и удовлетворяющую граничным условиям: а); б),.

Задача 6. Найти функцию гармоническую внутри полукругаеслина остальной части границы