Мета: ознайомитися з дифракцією Френеля від круглого отвору, визначити довжину світлової хвилі та радіуси зон Френеля.

Прилади і матеріали: програма комп’ютерної лабораторної роботи “Дифракція Френеля від круглого отвору”, лінійка.

Теоретичні відомості

Дифракція світла – оптичне явище, пов’язане із зміною напряму поширення світлових хвиль (порівняно з напрямом, передбаченим геометричною оптикою) та з просторовим перерозподілом їх інтенсивності під впливом перешкод і неоднорідностей середовища на їхньому шляху. Під дифракцією розуміють будь-яке відхилення від прямолінійного поширення світла, якщо воно не зумовлене відбиванням, заломленням або викривленням променів у середовищах, в яких показник заломлення безперервно змінюється. Дифракція світла зумовлена його хвильовою природою.

Дифракція світла пояснюється принципом Гюйгенса-Френеля: нескінчено малі елементи хвильової поверхні є джерелами вторинних сферичних когерентних хвиль, амплітуда яких пропорційна до площі елемента; амплітуда коливань в довільній точці простору за хвильовою поверхнею визначається суперпозицією таких вторинних хвиль.

Явища дифракції прийнято розрізняти залежно від відстані до перешкоди, встановленої на шляху поширення світла, до джерела і екрана, на якому спостерігається дифракційна картина. Якщо ці відстані, чи одна з них, не дуже великі, то дифракційні явища називають дифракцією Френеля (дифракція сферичних хвиль) або дифракцією в непаралельних променях.

Дифракція Фраунгофера (дифракція в паралельних променях) – дифракція світла, що спостерігається на таких відстанях, для яких кутові розміри оптичних неоднорідностей набагато менші ніж відношення довжини світлової хвилі до лінійних розмірів цих неоднорідностей. Між дифракціями Френеля і Фраунгофера не існує принципової різниці і різкої межі.

Робоча формула

Розглянемо проходження світла через круглий отвір DD (рис. 68.1). Проведемо з точки О конічні поверхні M₁OM₁^′, M₂OM₂^′, M₃OM₃^′ і т. д. до перетину з поверхнею сферичної хвилі DM₀D. Довжини їх виберемо так, що відстань від точок M₀, M₁, M₂, … до точки О збільшується на довжину півхвилі світла, що падає на отвір ( , , …, ). Утворені конуси поділять поверхню DM₀D на сукупність рівновеликих кільцевих зон (зон Френеля).

В

Рисунок 1

изначимо висоту сегмента h_j. З трикутників SM_jC і CM_jO маємо

,

з відки

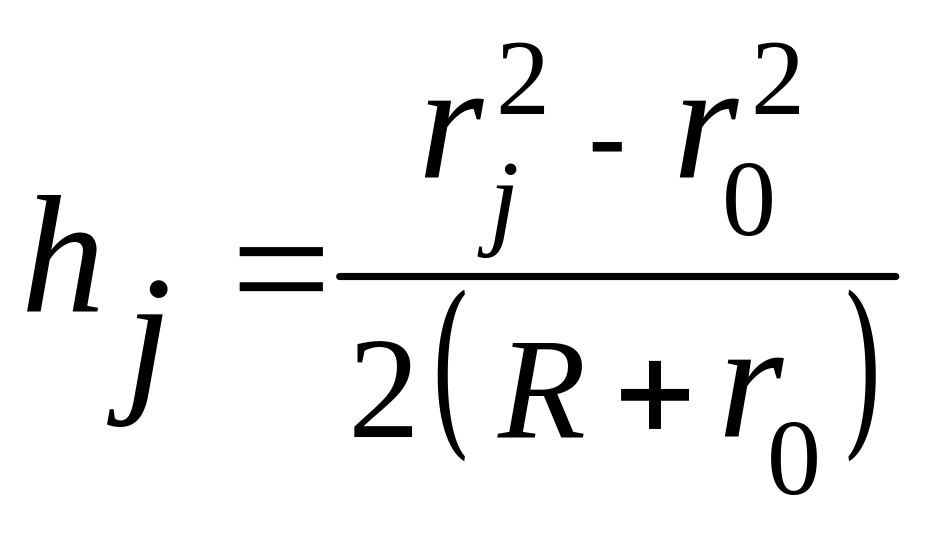. (68.1)

Оскільки , то . Якщо і , то членом можна знехтувати і тоді .

Підставивши цей вираз у формулу (68.1), одержимо

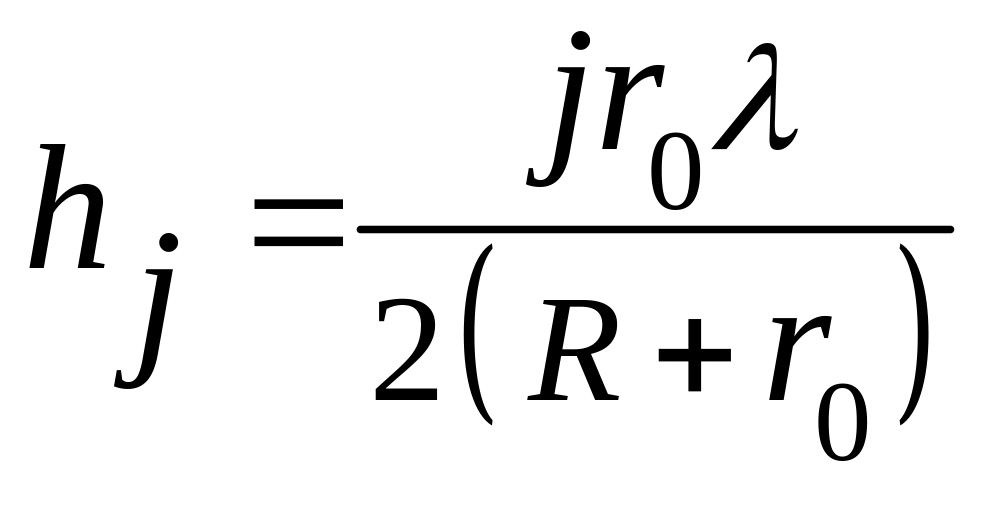. (68.2)

Визначимо кількість зон Френеля j, що вміщуються в отворі екрана. З рисунку 68.1 маємо

.

Оскільки , то величиною можна знехтувати.

Враховуючи, що та формулу (68.2), отримаємо

. (68.3)

Радіус останньої зони Френеля збігається з радіусом отвору, тобто . Тоді кількість зон Френеля n обчислимо за формулою

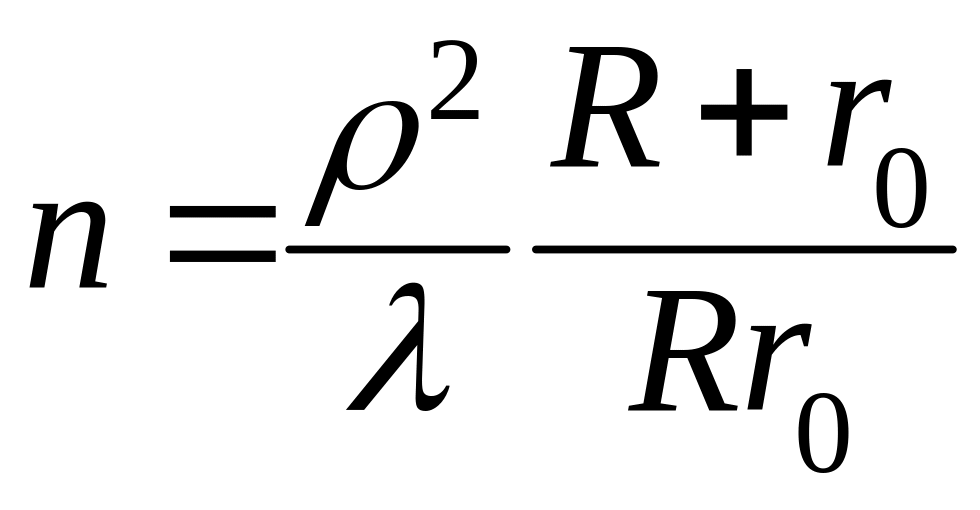. (68.4)

С вітлові хвилі від першої і другої зон, дійшовши до точки О, будуть взаємно послаблятися, так що в точці О дія першої зони практично знищується дією другої зони, дія другої зони протилежна до дії третьої зони і т. д. Якщо отвір DD такий, що в ньому вміщується тільки дві зони, то в точці О практично не буде світла (дві сусідні зони взаємно послаблюють одна одну). Отже, ми побачимо на екрані в центрі темний круг, оточений світлим кільцем. Для отвору в якому вкладається три зони Френеля на екрані в центрі буде світлий круг, оточений темним кільцем, за яким знову буде світле кільце. В загальному, за парної кількості зон, в центрі буде темне кільце, оточене почергово світлими і темними кільцями; за непарної кількості зон – у центрі буде світлий круг, почергово оточений темними і світлими кільцями. Чим більший отвір, тим розміри кілець будуть меншими.

Т

Рисунок 68.2

ак як розміри зон Френеля залежать від довжини світлової хвилі, то і вигляд дифракційної картини буде залежати від довжини хвилі.

Для малих кутів дифракції φ (рисунок 68.2) сумарна амплітуда виражається через спеціальну функцію Бесселя , де , r–радіус отвору, φ – кут дифракції. Корінь, що відповідає першому мінімуму інтенсивності, тобто визначає кутові розміри центральної світлої плями, визначається з умови

. (68.5)

Ця формула відіграє першорядну роль у дифракційній теорії оптичних приладів. Кутові радіуси темних кілець наближено визначаються формулою

, де m=1, 2, 3, ... (68.6)

Лінійні розміри радіуса першого темного кільця приблизно дорівнюють

. (68.7)

де L – відстань від отвору до екрана.