2 Числа, кодування і арифметика

2.1 Двійкові числа

Цифрові обчислювальні машини працюють з двійковими числами. Двійкова система відліку або система з основою 2 використовує тільки цифри 0 і 1. Ці двійкові числа названі бітами ( від binary digit). Фізично в цифрових електронних системах біт 0 представлено напругою LOW ( низька ), а біт 1 – напругою HIGH ( висока ).

Людська діяльність пропонує використання десяткової системи відліку. Десяткова система, або система з основою 10, містить 10 цифр ( від 0 до 9). Вона також характеризується значенням позиції ( або вагою ). В табл.2.1 наведено приклад, де десяткове число 2496 рівне двом тисячам, плюс чотири сотні, плюс дев’ять десятків, плюс шість одиниць ( 2000 + 400 + 90 + 6 = 2496 ).

Двійкова система має також властивість вирівнювання. В табл.2.2 наведено десяткові значення перших чотирьох двійкових позицій. Двійкове число 1010 (вимовляється: один, нуль, один, нуль) перетворено, таким чином, в свій десятковий еквівалент 10. Біт нуля двійкового числа в табл.2.2 називається молодшим бітом (МБ), біт вісімки – старшим бітом (СБ).

Таблиця 2.1 Значення позицій десяткових чисел

Степінь основи	103 102 101 100
Значення позицій	1000 100 10 1
Десяткові	2 4 9 6 2000 + 400 + 90 + 6 = 2496

Таблиця 2.2 Значення позицій двійкових чисел

Степінь основи	23 22 21 20
Значення позицій	8 4 2 1
Двійкові Десяткові	СБ МБ 1 0 1 0 8 + 0 + 2 + 0 = 10

В табл.2.3 наведені десяткові числа від 0 до 15, а також їх двійкові еквіваленти. Програмісти повинні запам’ятати ці двійкові числа.

Таблиця 2.3 Десяткові числа і їх двійкові еквіваленти

Десяткові	Двійкові	Десяткові	Двійкові
10 1	8 4 2 1	10 1	8 4 2 1
0 1 2 3 4 5 6 7	0 1 1 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	8 9 1 0 1 1 1 2 1 3 1 4 1 5	1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1

Як перетворити двійкове число 10110110 в його десятковий еквівалент? Процедура перетворення виконується у відповідності з табл.2.4. Десяткові значення кожної позиції записані під кожним бітом, потім десяткові числа додають ( 128 + 32 + 16 +4 +2 = 182 ), що дає 182.

Таблиця 2.4 Двійково – десяткове перетворення

Степінь основи	27	26	25		24	23	22		21	20
Значення позицій	128	64	32		16	8	4		2	1
Двійкове Десяткове	1 128	+	1 32	+	1 16	+	1 4	+	1 2	=	182

Основа системи відліку вказується індексами. Таким чином, число 10110110₂ є двійковим ( або з основою 2 ) , а число 182₁₀ – десятковим: 10110110₂ = 182₁₀.

Я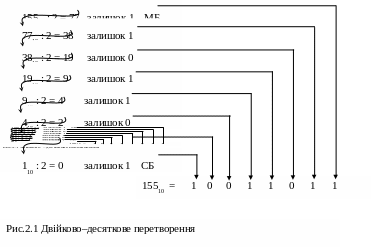 к перетворити десяткове 155 в його двійковий еквівалент? Процедура переведення наведена на рис.2.1.

Десяткове 155 спочатку ділиться на 2, що дає нам частку 77 і залишок 1. Цей залишок стає МБ двійкового числа і розміщується в цю позицію ( див. рис 2.1 ). Потім частка ( 77 ) переміщується, як показує стрілка, і стає наступним діленим. Потім кожна частка послідовно ділиться на 2 до тих пір, доки не маємо частку рівну 0, і залишок, рівний 1 ( див. передостанній рядок на рис.2.1 ). Останній рядок на рис.2.1 дає нам результат 155₁₀ = 100110111₂.

Вправи:

1. Цифрова ЕОМ використовує ________ систему.

2. В двійковій системі біт значить ________ __________.

3. Число 100₁₀ є _________ числом.

4. Записати двійкове число один, один, нуль, нуль в цифровій формі.

5. Що значить скорочення МБ?

6. Перетворити в десятковий код наступні двійкові числа:

а) 0001₂ = б) 0101₂ = в) 1000₂ = г) 1011₂ =

д) 1111₂ = е) 0111₂ =

7. Перетворити в десятковий код наступні двійкові числа:

а) 1000 0000₂ = б) 0001 0000₂ = в) 0011 0011₂ =

г) 0110 0100₂ = д) 0001 1111₂ = е) 1111 1111₂ =

8. Перетворити в двійковий код наступні десяткові числа:

а) 23₁₀ = б) 39₁₀ = в) 55₁₀ = г) 48₁₀ = д) 204₁₀ = .