
- •Функції багатьох змінних
- •Диференціальні рівняння
- •9.1. Означення диференціального рівняння та його розв’язання
- •9.2. Способи розв’язання звичайних диференціальних рівнянь першого порядку
- •9.2.1. Спосіб розв’язання звичайного диференціального рівняння першого порядку, яке допускає відокремлення змінних
- •Спосіб розв’язання однорідного звичайного диференціального рівняння першого порядку
- •Спосіб розв’язання лінійного звичайного диференціального рівняння першого порядку
- •9.3. Способи розв’язання звичайних диференціальних рівнянь вищих порядків, які допускають пониження порядку
- •9.4. Способи розв’язання звичайних диференціальних рівнянь другого порядку, які мають сталі коефіцієнти
- •9.5. Варіанти контрольних робіт
8.20.3.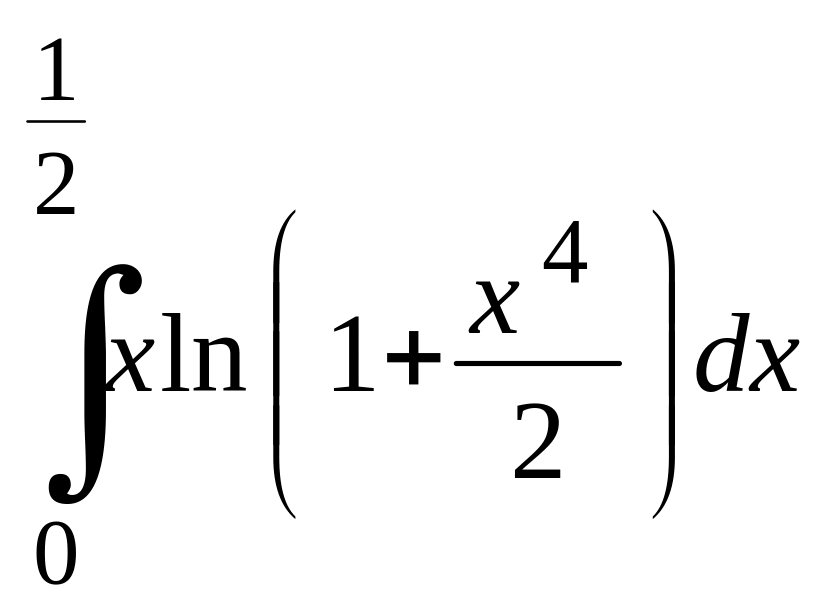 ; 8.20.4.
; 8.20.4.
![]()
Р о з д і л 3
Функції багатьох змінних
Ч а с т и н а 9
Диференціальні рівняння
9.1. Означення диференціального рівняння та його розв’язання
Рівняння,
яке містить незалежну змінну х, функцію
![]() та похідні будь-якого порядку цієї
функції, тобто рівняння
та похідні будь-якого порядку цієї
функції, тобто рівняння
![]() ,
називається диференціальним рівнянням.
,
називається диференціальним рівнянням.
Якщо функції, які входять до диференціального рівняння, залежать від однієї змінної, то диференціальне рівняння називається звичайним.
Порядок диференціального рівняння визначається найбільшим порядком похідної функції, яка входить до цього рівняння.
Функція, яка задовольняє диференціальне рівняння, тобто перетворює його в тотожність, називається розв’язком (інтегралом) диференціального рівняння.
Оскільки визначення розв’язку диференціального рівняння пов’язане з інтегруванням функцій, внаслідок якого отримуємо множину первинних функцій, які відрізняються одна від одної на деяку сталу, то функція, яка є розв’язком диференціального рівняння, включає в себе таку кількість сталих, яка відповідає порядку диференціального рівняння.
Розв’язок диференціального рівняння, який містить таку кількість сталих, яка відповідає порядку диференціального рівняння, називається загальним інтегралом (загальним розв’язком), а функція, яка буде отримана із загального інтеграла при числових значеннях сталих, називається частковим інтегралом цього рівняння.
Геометричне тлумачення часового інтеграла диференціального рівняння є кривою, графік якої називається інтегральною кривою цього рівняння, а загальному інтегралу відповідає сукупність всіх інтегральних кривих.
Відшукання
часткового інтеграла диференціального
рівняння n-го
порядку, який задовольняє початкові
умови
![]()
![]()
![]() ,
називається задачею
Коші.
,
називається задачею
Коші.
9.2. Способи розв’язання звичайних диференціальних рівнянь першого порядку
Способи розв’язання звичайних диференціальних рівнянь першого порядку пов’язані з видом диференціального рівняння. Розглядають такі види звичайних диференціальних рівнянь першого порядку: рівняння, які допускають відокремлювання змінних; однорідні рівняння; лінійні рівняння; рівняння Бернуллі.
Тому при розгляді поданого звичайного диференціального рівняння першого порядку з метою його розв’язання перш за все необхідно встановити його вид.
9.2.1. Спосіб розв’язання звичайного диференціального рівняння першого порядку, яке допускає відокремлення змінних
Диференціальне рівняння першого порядку, яке має вигляд
![]() ,
,
де
![]() та
та
![]() можуть бути подані у вигляді добутку
двох функцій, кожна з яких залежить
тільки від однієї змінної,
тобто
можуть бути подані у вигляді добутку
двох функцій, кожна з яких залежить
тільки від однієї змінної,
тобто
![]() ;
;
![]() ,
називається звичайним диференціальним
рівнянням першого порядку, яке допускає
відокремлення змінних.
,
називається звичайним диференціальним
рівнянням першого порядку, яке допускає
відокремлення змінних.
Тоді маємо
![]() ,
,
а
якщо почленно поділити на
![]() ,
то
,
то
![]() ,
,
тобто при такому перетворенні досягається відокремлення змінних.
Відшукання загального інтеграла рівняння досягається почленним інтегруванням, а саме
![]() .
.
Задача 9.1. Знайти загальний інтеграл рівняння
![]() .
.
Розв’язання. Маємо
![]()
та
після почленного ділення на
![]()
![]() .
.
Почленне інтегрування дозволяє визначити загальний інтеграл рівняння:
![]() ;
;
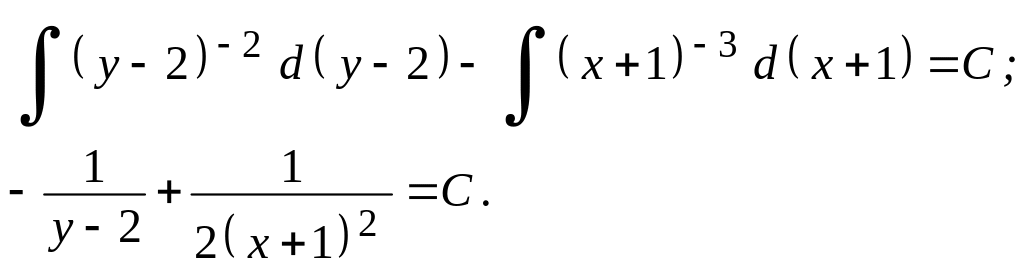
Задача 9.2. Знайти загальний інтеграл рівняння
![]() .
.
Розв’язання. Маємо
,
та після почленного ділення на xy
![]() ;
;
![]() .
.
Почленне інтегрування дозволяє визначити загальний інтеграл рівняння, а саме:
![]()
![]()
Задача 9.3. Знайти загальний інтеграл рівняння
![]() .
.
Розв’язання. Маємо
![]() .
.
Поділимо
почленно на добуток
![]() ,
тоді
,
тоді
![]() ;
;
![]()
![]()
![]() .
.
