2. Зміст роботи

2. 1. Розрахунок динамічних характеристик ланки другого порядку за допомогою Mathcad.

2.2. Побудова графіків динамічних характеристик коливальної ланки.

3. Запис математичної моделі коливальної ланки

Прикладом ланки другого порядку є електричне коло електродвигуна із врахуванням маси якоря. Досліджуємо електродвигун постійного струму з незалежним збудженням з регулюванням по колу якоря рис.1. Вхідна величина U_вх – напруга на якорі , вихідна – частота обертання вала якоря ω. Параметри обмотки якоря , ом; L_я, Гн. Робота електродвигуна в перехідному процесі описується основним рівнянням динаміки

(17)

та рівняння електричної рівноваги в колі якоря

(18)

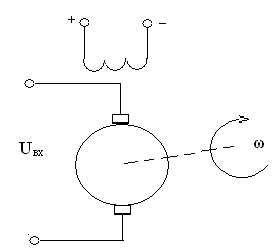
Рис.1. Принципова та функціональна схеми ланки "електричний двигун"

де J –момент інерції якоря;

𝜔- частота обертання вала якоря;

M_д – обертовий момент двигуна;

M_о – момент опору на валу двигуна;

- вхідна напруга, прикладена до якоря; − е.р.с. обмотки якоря;

r_я – активний опір кола якоря (включаючи і опір джерела живлення U);

L_я − індуктивність кола якоря .

Так як двигун має незалежне постійне збудження і постійний магнітний потік Ф= соnst, то пропорційна частоті обертання 𝜔.

= С_𝜔 𝜔, (19)

де С_𝜔 = С∙Ф − конструктивна постійна;

Ф – магнітний потік головних полюсів.

Підставимо значення в рівняння (19), одержимо:

(20)

Рушійний момент двигуна визначається з виразу

М_д= С_мi_яФ. (21)

Момент опору умовно можна виразити через струм i_с, що відповідає моменту опору:

М_о= С_мi_сФ_, (22)

де С_м = - конструктивна постійна. Підставляючи (21) і (22) в (17) одержуємо (23)

Знаходимо з цього рівняння значення струму якоря і його похідної

; (24)

і підставимо їх в рівняння (20),одержимо

(25)

Розділимо все рівняння на , помножимо і розділимо перший член лівої частини на r_я, одержимо:

(26)

Введемо наступні позначення:

- електромеханічна постійна часу двигуна, сек.; (27)

- електромагнітна постійна часу кола якоря двигуна, сек; (28)

-коефіцієнт підсилення двигуна. (29)

Введемо позначення ;

Після підстановки вказаних позначень отримаємо диференційне рівняння

(30)

Якщо двигун працює вхолосту, то

(31)

Коефіцієнт згасання знаходимо з (30)

𝜉= (32 )

_{В операторній формі рівняння двигуна набуває вигляд}

_{Характеристичне рівняння ланки .}

Корені характеристичного рівняння ланки можна визначити за допомогою функції Mathcad polyroots .

Для цього необхідно записати в вектор аргумента функції polyroots

коефіцієнти характеристичного рівняння наступним чином v=(1 2*𝜉*T T²)^T .

_{Значення корен}ів будуть виведені в значенні " polyroots=" .

Полярний момент інерції, Н∙м² J= ,

де 𝐺 − вага якоря електродвигуна, Н;

𝐷 − діаметр якоря електродвигуна, м.

Параметри варіантів ланки для виконання лабораторної роботи приведені в таблиці 1.

Таблиця 1.1. Параметри ланки

Параметри ланки	Робочі місця
	1	2	3	4	5	6	7	8
,ом	0.122	0.0437	0.043	0.127	0.119	0.124	0.044	0.048
,мГн	10	12	14	16	18	20	22	24
𝐺, кН	17,3	3,44	13,42	13,95	6,10	7,50	4,00	5,00
𝐷, м	0.74	0.66	0.67	0.68	0.7	0.72	0.76	0.78
	100	105	110	115	120	125	130	135