
- •1. Короткий опис
- •2. Вказівки до виконання роботи
- •3. Зміст роботи
- •4. Порядок виконання роботи
- •6. Питання для контролю
- •1. Короткий опис
- •2. Зміст роботи
- •3. Запис математичної моделі ланки другого порядку
- •4. Порядок виконання роботи
- •6. Питання для контролю
- •1. Короткий опис
- •2. Зміст роботи
- •3. Запис математичної моделі коливальної ланки
- •4. Порядок виконання роботи
- •6. Питання для контролю
- •1. Короткий опис.
- •3. Порядок виконання роботи
- •5. Питання для контролю
- •1.Математична модель системи
- •2. Зміст роботи
- •3. Порядок виконання роботи.
- •5. Питання для контролю.
- •2.Зміст роботи
- •3.Порядок виконання роботи:
- •5.Питання для самоконтролю
- •1.Структурна схема та математична модель сар.
- •2. Вихідні дані для виконання лабораторної роботи
- •3. Порядок виконання роботи
- •Запитання для самоконтролю
- •3.Порядок виконання роботи
- •Питання для самоконтролю
- •Використана література
- •Дубравін Юрій Федорович Теорія систем автоматичного управління
- •03049, Київ – 49, вул. Миколи Лукашевича, 19
4. Порядок виконання роботи
Параметри ланки для виконання роботи задаються викладачем. Після запуску Mathcad необхідно:
ввести вихідні дані ланки ;
задати інтервал зміни часу в межах 0 –0.5 с., з кроком зміни 0.01, с.;
задати інтервал зміни частоти в межах 0 – 1000 1/с та кроком 2, 1/с.;
виконати розрахунок наступних параметрів:
коренів
характеристичного рівняння р1,2
постійної часу Т , коефіцієнта згасання
𝜉
, постійні
часу послідовно з’єднаних аперіодичних
ланок
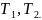
Розрахувати наступні функції: –дійсну частотну характеристику; –уявну частотну характеристику;
− модуль ланки (АЧХ);
− аргумент ланки (ФЧХ);
логарифмічну амплітудно-частотну характеристику (ЛАЧХ);
− перехідну функцію ланки;
Побудувати годограф АФХ та графіки розрахованих функцій.
5. Зміст звіту
5. 1. Схема і математична модель ланки.
5. 2. Таблиці результатів розрахунку функцій ланки.
5. 3. Годограф АФХ та графіки розрахованих функцій.
6. Питання для контролю
6. 1. При виконанні яких умов ланку другого порядку можна представити у вигляді послідовно з'єднаних аперіодичних ланок ?
6. 2. Як побудувати годографі АФХ ?
6. 3. Як одержати КПФ ?
6.4. Як впливає на перехідну функцію ланки величина ємності конденсатора С ?
Лабораторна робота № 3. Дослідження коливальної ланки
Мета роботи: Дослідження динамічних характеристик коливальної анки.
1. Короткий опис
Коливальна
ланка
описуються
диференціальним рівнянням другого
порядку, аналогічним рівнянню аперіодичної
ланки другого порядку

 (1)
(1)
Передавальна
функція ланки:
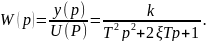 (2)
(2)
Характеристичне рівняння ланки: T2p2 + 2ξTp + 1 = 0 . (3)
Відносний коефіцієнт згасання для коливальної ланки знаходиться у діапазоні 0 < ξ < 1 . Корені характеристичного рівняння (3) вказаної ланки різні, комплексно-сполучені, з негативною дійсною частиною:
(4)
Комплексна передавальна функція (КПФ) ланки
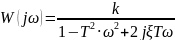 (5)
(5)
Модуль КПФ знаходимо згідно правилу: модуль добутку комплексних чисел дорівнює добутку їх модулів
 .
(6)
.
(6)
Аргумент КПФ знаходимо згідно правилу: аргумент добутку комплексних чисел дорівнює сумі аргументів співмножників
 (7)
Дійсна
частина КПФ
(7)
Дійсна
частина КПФ
 (8)
(8)
Уявна
частина КПФ
Q(𝜔)= (9)
(9)
Логарифмічна амплітудно-частотнa характеристикa (ЛАЧХ)
 (10)
(10)
Кутова
частота власних коливань
ланки
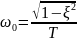 (11)
(11)
Декремент
затухання наступний:
 (12)
Резонансна частота
(12)
Резонансна частота
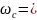
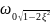 .
(13)
.
(13)
Початкова
фаза коливань
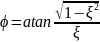 .
(14)
.
(14)
Введемо
позначення
 .
(15)
.
(15)
Перехідна функція ланки з урахуванням (11,12,13,15) має вигляд:
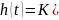 (16)
(16)
